Too big model ?! Deep compress it !
在深度学习的各个领域有很多意义长远的研究,但有一个方向是最有挑战性,所带来的影响也会辐射到深度学习的各种应用,那就是研究深度学习本身。
今天给大家带来的论文是一篇斯坦佛大学 songhan的:
该篇论文是ICLR2016最佳论文,不论是从idea到行文风格,都是难得一见的好文,建议大家去读原文。
论文出发点:
VGG16应该是大家接触深度学习最基础的网络结构之一,从lenet 到 alexnet 再到VGG系列可以说是深度模型不顾一切向深发展的历程,直到VGG系列,大家发现,随着网络参数的增加,模型越来越大,当VGG系列的模型达到1G的时候,大家认识到这种超大的模型严重限制了各种应用,所以在后来的研究中不止再往深发展,而是尝试让模型更小,所以GoogLeNet(请注意我对L的大写,看不懂其中含义请面壁)尝试使用小的卷积核代替大的,在模型更深的时候也保证了参数的大小,后来的resnet将网络加深到了1000层的时候,性能提升了很多,这时,有人提出疑问,我们学习了这么多的参数,真的都有用吗?
拿最基本的全连接来说,两层的网络结构直接进行全连接,但是所有都连接起来真的有用吗?这篇论文告诉你答案! 你网络连接的大多数都是在无用功 useful work!!
好多研究方向都在尝试让网络的训练时间更多,比如师弟以前讲过的对卷积操作做优化,不论是从高性能并行进行加速,还是im2col技巧,都是泡沫,都是泡沫,在这篇卷积网络的论文中,我们压根不做卷积操作。。。
策略:
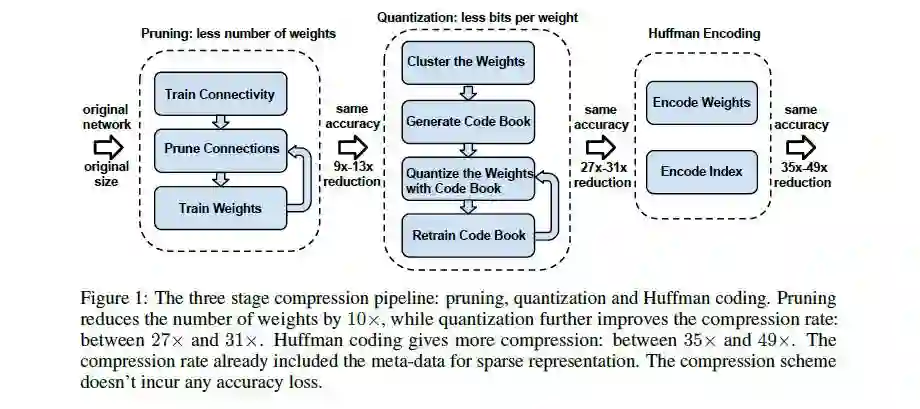
看题目我们就可以知道这篇论文有三个idea:
Prunes the network:只保留一些重要的连接;
Quantize the weights:通过权值量化来共享一些weights;
Huffman coding:通过霍夫曼编码进一步压缩;
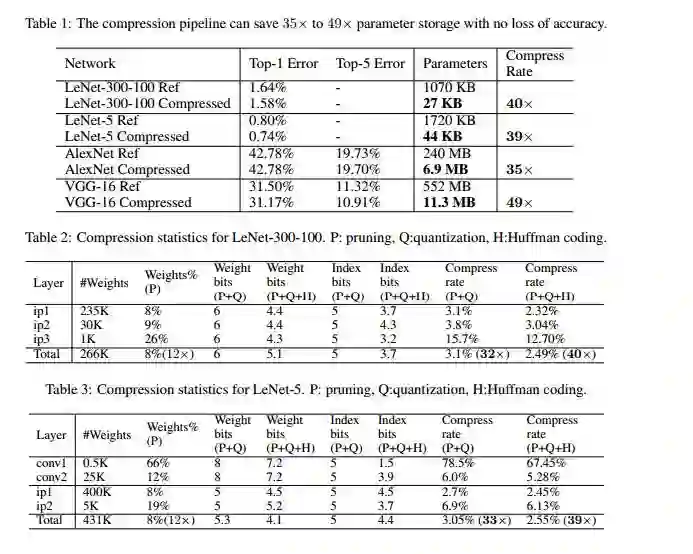
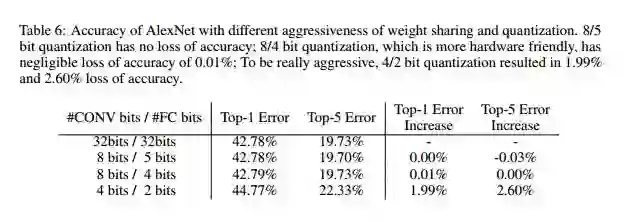
先放一下实验效果镇楼
Pruning:把连接数减少到原来的 1/13~1/9;
Quantization:每一个连接从原来的 32bits 减少到 5bits;
感受不到效果?这么看:
- 把AlextNet压缩了35倍,从 240MB,减小到 6.9MB;
- 把VGG-16压缩了49倍,从 552MB 减小到 11.3MB;
网络剪枝:
研究过树系列算法的人应该很知道剪枝操作,这种操作的提出是为了防止过拟合而对所学习的树进行修剪。同样在深度学习里我们有没有可能修剪掉网络里不重要的连接?答案是肯定的。
众所周知,在深度学习里的网络权重代表着一个神经元的重要性,那么权重值灰常低的神经元我们是不是可以不要了?
对,就是这么简单,本论文的剪枝就是这么做的。。
方法:
正常的训练一个网络;
把一些权值很小的连接进行剪枝:通过一个阈值来剪枝;
retrain 这个剪完枝的稀疏连接的网络;
Trained Quantization and Weight Sharing
学计算机组成原理的时候大家知道浮点数和整数的存储是不一样的,浮点数需要更多的空间来存储,从上个剪枝策略中我们发现连接可以剪枝,那么权重值本身能不能压缩呢?
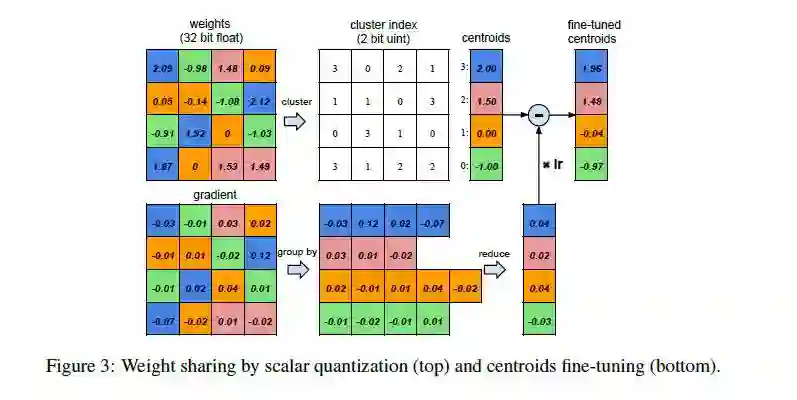
答案是可以的,作者的策略是进行聚类,从上图的上侧可以看到权重原本使用浮点数进行存储,现在我们本层的权重进行聚类,比如我们聚成4个类别,代表图中上侧的四种颜色,得到了这个聚类核,原本的矩阵我们不再存权重,而是存聚类核的索引,这样在存储上都是存储的int类型,而网络所有的权重共享聚类结果,所以我们在例子中我们原本需要32bit存储权重,16层就需要32*16,而这样做,我们只需要2*16+8 8是聚类中心!!
看起来也挺简单的。。
这么设计权重怎么更新?
看上图的下侧,所有传回来的梯度按聚类中心分组,然后组内相加,得出一个梯度中心,然后在用这个梯度中心和权重中心按学习率相减就完成了一次更新。超赞。
怎么聚类?
就用k-means!
注意,在网络中一个层是共享一个聚类中心的,但是在不同层之间不共享,不过 you can try it..
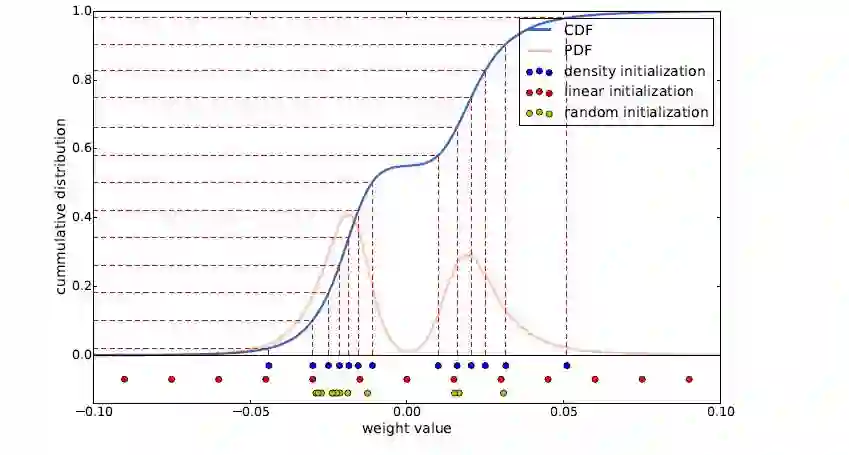
当然还有一些细节上的东西,比如k-means对聚类点初试点是非常敏感的,大家可以看到虽然这个聚类中心可以学习更新,但是初始化对其有很大的影响呢?
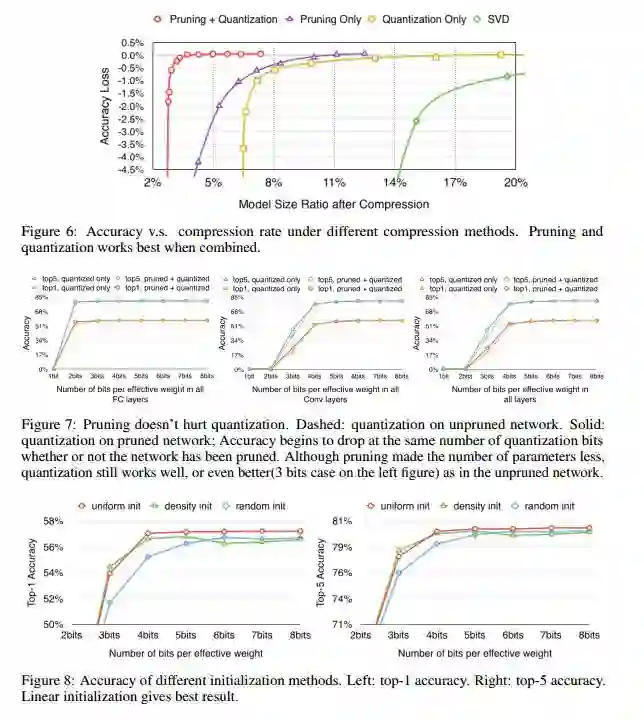
作者做了一个小实验:
用了五种初始化的方法,感觉属于k-means的东西,有时间可以深入的搞一下。
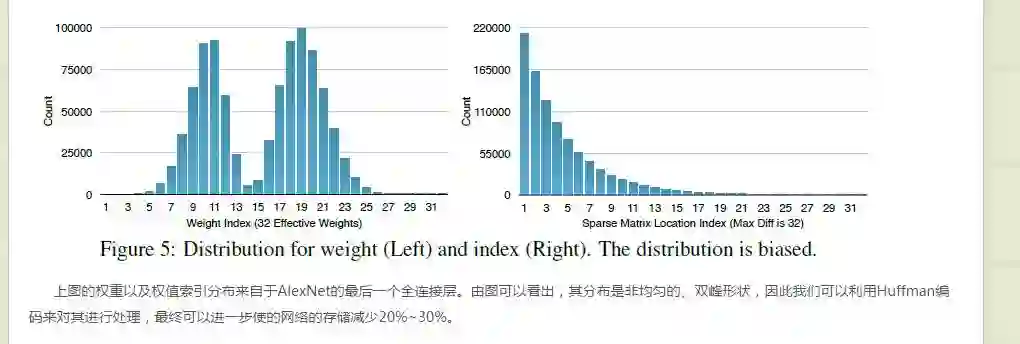
哈夫曼编码:
作者调取了最后全连接层权重的分布进行了统计,注意,权重都被我们聚类的一个中心了,所以最后的全连接层的分布的范围就是我们聚类的数目,从最终的结果发现,这个分布很。。l朴素? 好吧就用这个词了,就像一个高斯可以用一个高斯分布进行量化一样,而对于这种分布可以用哈夫曼进行编码,原文:
这个哈夫曼编码具体编码。有点弄不懂,大家讨论。
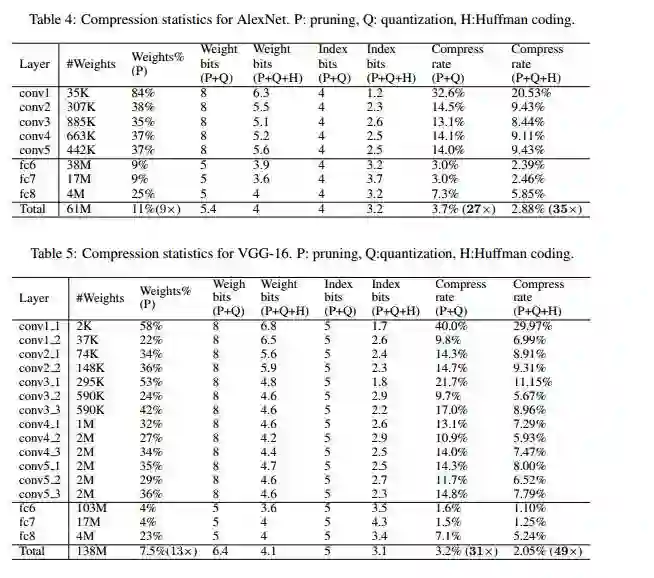
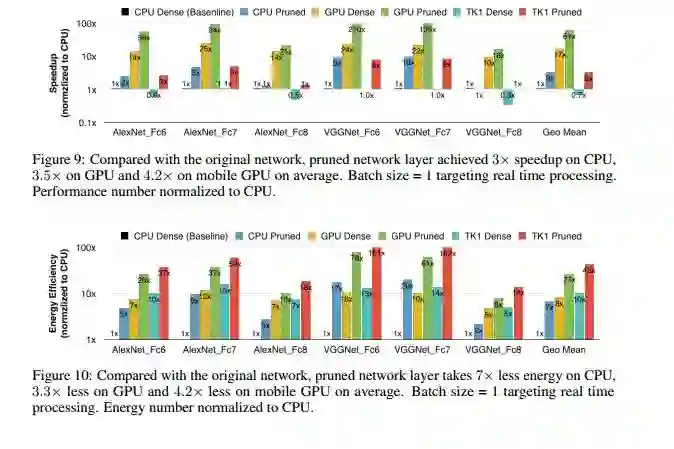
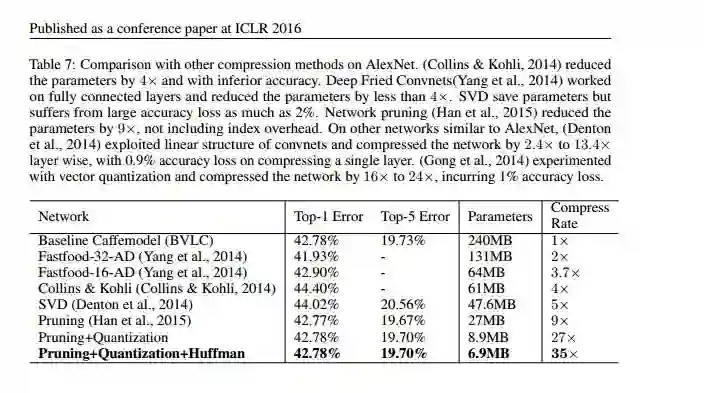
一大波实验来袭:
总结:
这篇论文非常棒,但是需要很强的工程实现。