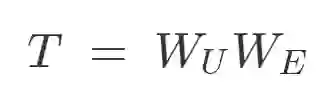经逆向工程，Transformer「翻译」成数学框架 | 25位学者撰文

机器之心报道

编辑：陈萍、杜伟

一篇多达 25 位研究者参与撰写的论文，以最简单的架构仅包含注意力块的两层或更少层的 transformer 模型为基础，对 Transformer 进行逆向研究。

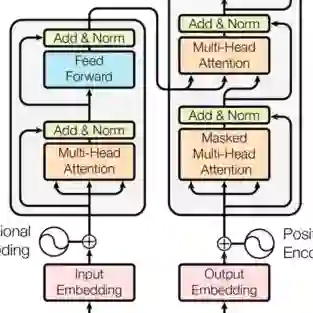
Transformer 是 Google 团队在 2017 年 6 月提出的 NLP 经典之作，由 Ashish Vaswani 等人在论文《 Attention Is All You Need 》中提出。自 Transformer 出现以来，便在 NLP、CV、语音、生物、化学等领域引起了诸多进展。

Transformer 在现实世界中的应用越来越广泛，例如 GPT-3 、LaMDA 、Codex 等都是基于 Transformer 架构构建的。然而，随着基于 Transformer 模型的扩展，其开放性和高容量为意想不到的甚至有害的行为创造了越来越大的空间。即使在大型模型训练完成数年后，创建者和用户也会经常发现以前从来没见过的模型问题。

解决这些问题的一个途径是机械的可解释性（mechanistic interpretability），即对 transformers 计算过程进行逆向工程，这有点类似于程序员如何尝试将复杂的二进制文件逆向工程为人类可读的源代码。

 如果逆向工程可行，那么我们就会有更系统的方法来解释当前模型的安全问题、识别问题，甚至可能预见未来尚未构建的模型安全问题。这有点类似于将 Transformer 的黑箱操作进行逆向，让这一过程变得清晰可见。之前有研究者开发了 Distill Circuits thread 项目，曾尝试对视觉模型进行逆向工程，但到目前为止还没有可比的 transformer 或语言模型进行逆向工程研究。

在本文中，由 25 位研究者参与撰写的论文，尝试采用最原始的步骤逆向 transformer。该论文由 Chris Olah 起草，Chris Olah 任职于 Anthropic 人工智能安全和研究公司，主要从事逆向工程神经网络研究。之后 Neel Nanda 对论文初稿进行了重大修改，Nanda 目前是 DeepMind 的一名研究工程实习生。Nelson Elhage 对论文进行了详细的编辑以提高论文章节清晰度，Nelson Elhage 曾任职于 Stripe 科技公司。

左：Neel Nanda；右：Christopher Olah

考虑到语言模型的复杂性高和规模大等特点，该研究发现，从最简单的模型开始逆向 transformer 最有效果。该研究旨在发现简单算法模式、主题（motifs）或是框架，然后将其应用于更复杂、更大的模型。具体来说，他们的研究范围仅包括只有注意力块的两层或更少层的 transformer 模型。这与 GPT-3 这样的 transformer 模型形成鲜明的对比，GPT-3 层数多达 96 层。

论文地址：https://transformer-circuits.pub/2021/framework/index.html#acknowledgments

该研究发现，通过以一种新的但数学上等效的方式概念化 transformer 操作，我们能够理解这些小模型并深入了解它们的内部运作方式。值得注意的是，研究发现特定的注意头，本文称之为归纳头（induction heads），可以在这些小模型中解释上下文学习，而且这些注意力头只在至少有两个注意层的模型中发展。此外，该研究还介绍了这些注意力头对特定数据进行操作的一些示例。

各章节内容概览

为了探索逆向工程 transformers 面临哪些挑战，研究者对几个 attention-only 的 toy 模型进行了逆向功能。

首先是零层 transformers 模型的二元统计。研究者发现，二元表可以直接通过权重访问。

在讨论更复杂的模型之前，考虑零层（zero layer）transformer 很有用。这类模型接受一个 token，嵌入，再取消嵌入，以生成预测下一个 token 的 logits

由于这类模型无法从其他 tokens 传输信息，因此只能从当前 token 预测下一个 token。这意味着，W_UW_E 的最优行为是近似二元对数似然。

零层 attention-only transformers 模型。

其次，单层 attention-only transformers 是二元和 skip 三元模型的集合。同零层 transformers 一样，二元和 skip 三元表可以直接通过权重访问，无需运行模型。这些 skip 三元模型的表达能力惊人，包括实现一种非常简单的上下文内学习。

对于单层 attention-only transformers 模型，有哪些路径扩展（path expansion）技巧呢？研究者提供了一些。

如下图所示，单层 attention-only transformers 由一个 token 嵌入组成，后接一个注意力层（单独应用注意力头），最后是解除嵌入：

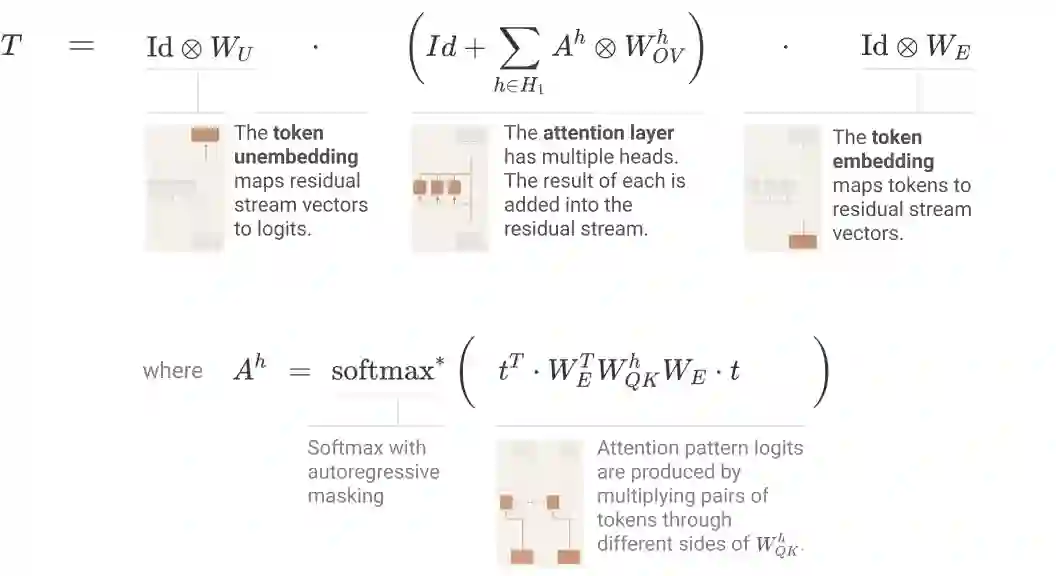
使用之前得到的张量标记（tensor notation）和注意力头的替代表征，研究者可以将 transformer 表征为三个项的乘积，具体如下图所示：

研究者采用的核心技巧是简单地扩展乘积，即将乘积（每个项对应一个层）转换为一个和，其中每个项对应一个端到端路径。他们表示，每个端到端路径项都易于理解，可以独立地进行推理，并能够叠加组合创建模型行为。

最后，两层 attention-only transformers 模型可以使用注意力头组合实现复杂得多的算法。这些组合算法也可以直接通过权重检测出来。需要注意的是，两层模型适应注意力头组合创建「归纳头」（induction heads），这是一种非常通用的上下文内学习算法。

具体地，当注意力头有以下三种组合选择：

• Q - 组合：W_Q 在一个受前面头影响的子空间中读取；

• K - 组合：W_K 在一个受前面头影响的子空间中读取；

• V - 组合：W_V 在一个受前面头影响的子空间中读取。

研究者表示，Q - 和 K - 组合与 V - 组合截然不同。前两者都对注意力模式产生影响，允许注意力头表达复杂得多的模式。而 V - 组合对一个注意力头专注于某个给定位置时所要传输的信息产生影响。结果是，V - 组合头变现得更像一个单一单元，并可以考虑用来创建额外的「虚拟注意力头」。

对于 transformer 有一个最基础的问题，即「如何计算 logits」？与单层模型使用的方法一样，研究者写出了一个乘积，其中每个项在模型中都是一个层，并扩展以创建一个和，其中每个项在模型中都是一个端到端路径。

其中，直接路径项和单个头项与单层模型中的相同。最后的「虚拟注意力头」项对应于 V - 组合。虚拟注意力头在概念上非常有趣，但在实践中，研究者发现它们往往无法在小规模的两层模型中发挥重大作用。

此外，这些项中的每一个都对应于模型可以实现更复杂注意力模式的一种方式。在理论上，很难对它们进行推理。但当讨论到归纳头时，会很快在具体实例中用到它们。

© THE END 

转载请联系本公众号获得授权

投稿或寻求报道：content@jiqizhixin.com