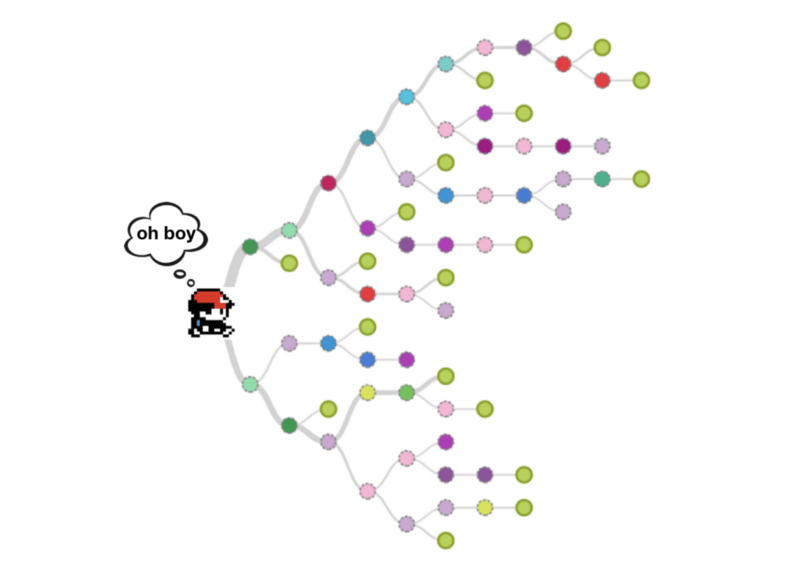
为什么AI可以通关马里奥，却玩不好精灵宝可梦？

来源：Medium

编译：weakish

编者按：数据科学家Shayaan Jagtap以马里奥和精灵宝可梦为例，解释了当前的AI还不擅长处理哪些种类的问题。

你大概早就听说机器能以超人的水平玩游戏。这些机器可能经过明确编程，对设定的输入作出反应，给出设定的输出，也可能自行学习（点击阅读）和演化（点击阅读），以不同的方式对相同的输入作出反应，希望找到最优的反应。

一些著名的例子：

• AlphaZero（点击阅读），24小时训练之后，成为地球上最强大的国际象棋选手。

• AlphaGo（点击阅读），著名的围棋机器人，击败了世界级棋手李世乭和柯洁。

• MarI/O，可自行学习以任意等级进行游戏的超级马里奥机器人。

这些游戏很复杂，训练上面的机器需要精心组合复杂的算法，反复模拟，大量时间。本文将重点讨论MarI/O，以及为何我们无法使用相似的方法通关精灵宝可梦游戏。如果你不了解MarI/O，可以看下这个演示视频：

在这方面，马里奥和精灵宝可梦有三个关键不同：

1. 目标数量

2. 分支因子

3. 全局优化与局部优化

目标数量

机器学习的方式是优化某种目标函数。不管它是最大化奖励函数（强化学习）、适应度函数（遗传算法），还是最小化代价函数（监督学习），目标都是类似的：取得尽可能好的分数。

马里奥只有一个目标：到达本级别的终点。简单来说，在死亡之前，到达的地方越靠右，表现就越好。这是一个单一的目标函数，模型的能力可以由这一个数字直接衡量。

精灵宝可梦的目标……有很多。击败精英4级？捕获所有宝可梦？训练最强团队？上面所有这些？还是其他完全不同的目标？

我们不仅需要定义什么是最终目标，还要定义进展看起来是什么样的？这样，任意时刻，大量可能选择之中的每种行动才能和奖励或损失对应起来。

这引出了下一项主题。

分支因子

简单说，分支因子是任意一步可以做出的可能选择数量。国际象棋的分支因子平均是35，围棋是250. 额外考虑的未来每一步，都有(分支因子)^步数项选择需要评估。

马里奥中，要么向左，要么向右，要么起跳，要么什么也不做。机器需要评估的选择数很小。同时，从算力上说，分支因子越小，机器人可以预计的步数就越多。

精灵宝可梦则是一个开放世界游戏，这意味着，任意给定时刻都有大量选择。简单的向上、向下、向左、向右无法有效计算分支因子数量。相反，我们需要查看下一个有意义的行动。下一个行动是进入战斗，和NPC交谈，还是进入左/右/上/下方的小地图？随着游戏的进行，可能的选择范围越来越大。

创建一个可以找到最佳选择组合的机器，需要考虑短期和长期目标，这引出了最后一项主题。

全局优化与局部优化

局部优化与全局优化既包括空间层面，也包括时间层面。短期目标和周围地理区域属于局部，长期目标和城市、全地图这样较大的区域属于全局。

拆分每一步可以是一种分解精灵宝可梦问题的方式。如何从A点到B点的局部优化是容易的，但决定哪个目的地是最优的B点则是一个困难得多的问题。贪心算法在这里无法奏效，因为局部最优的决策不一定导向全局最优。

马里奥地图很小，而且是线性的。而精灵宝可梦却有着错综复杂的非线性大地图。为了达到高阶目标，当前优先级会随着时间而改变，将全局目标转换为优先局部优化问题不是一项容易的任务。这不是我们当前的模型具有足够能力可以处理的事情。

最后一点

从机器人的角度来说，精灵宝可梦不是一个游戏。机器人都是专门的，当你遭遇要战斗的NPC时，帮助你在地图上移动的机器人对此束手无策——这是两个完全不同的任务。

在战斗阶段，每个回合有许多选项。选择如何移动，切换到哪个宝可梦，何时使用不同的物品，本身就是一个复杂的优化问题。我看到过一篇介绍如何创建战斗模拟器的文章，考虑得很周到，在没有考虑物品使用这一决定战斗结果的关键因素的前提下，复杂度已经高得惊人了。

目前，我们能够创造出能够在我们自己的游戏中战胜我们的机器人，我们该为此感到高兴。这些游戏在数学上很复杂，但在目标上很简单。随着AI技术的进展，我们将创造能够解决有越来越大影响力的真实世界问题的机器人，这些机器人将通过自行学习复杂优化问题来解决真实世界问题。可以放心的是，还是有很多事情我们要比机器更擅长，其中包括我们童年时玩的游戏——至少到目前为止是这样。感谢阅读！

原文地址：https://towardsdatascience.com/why-can-a-machine-beat-mario-but-not-pokemon-ff61313187e1