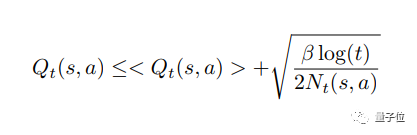一文带你理解Q-Learning的搜索策略，掌握强化学习最常用算法

王小新 编译自 Medium
量子位 出品 | 公众号 QbitAI

Q-Learning是强化学习中最常用的算法之一。

Medium上有篇文章，讨论了这种算法的一个重要部分：搜索策略。

量子位搬运过来，以下为博客译文：

我们先介绍下有关概念和符号。

强化学习

强化学习（Reinforcement Learning, RL）属于机器学习的一个分支，利用智能体（agent）通过状态感知、选择动作和接收奖励来与环境互动。每一步中，智能体都会通过观察环境状态，选择并执行一个动作，来改变其状态并获得奖励。

马尔可夫决策过程

在传统环境中，马尔可夫决策过程（Markov Decision Processes, MDP）可以解决不少RL问题。这里，我们不会深入讨论MDP的理论，有关MDP算法的更多内容可参考：

https://en.wikipedia.org/wiki/Markov_decision_process

我们用森林火灾来解释下MDP算法，代码实现可使用python MDP Toolbox：

http://pymdptoolbox.readthedocs.io/en/latest/api/example.html

森林管理包括两个动作，等待和砍伐。每年要做出一个决定，一是为林中动物保持古老森林，二是砍伐木材来而赚钱。而且，每年有p概率发生森林火灾，有1-p的概率为森林生长。

先定义MDP算法中一些参数S、A、P、R和γ，其中：

• S是状态空间（有限），包括3种不同年龄树木，年龄级分别为0-20年、21-40年和40年以上；

• A是动作空间（有限），即等待或砍伐；

• P和R分别是转移矩阵和奖励矩阵，很容易写出它的闭合形式；

• γ是数值在0与1之间的贴现因子，用来平衡短时和未来奖励的关系；

• 策略π是当前状态下决策的静态分布；

该模型的目标是在未给出MDP动态知识的情况下找到一个最优策略π*。

要注意，如果具有这个动态知识，直接用最优值迭代方法就能找到最优策略。

 1def optimal_value_iteration(mdp, V0, num_iterations, epsilon=0.0001):
 2    V = np.zeros((num_iterations+1, mdp.S))
 3    V[0][:] = np.ones(mdp.S)*V0
 4    X = np.zeros((num_iterations+1, mdp.A, mdp.S))
 5    star = np.zeros((num_iterations+1,mdp.S))
 6    for k in range(num_iterations):
 7        for s in range(mdp.S):
 8            for a in range(mdp.A):
 9                X[k+1][a][s] = mdp.R[a][s] + mdp.discount*np.sum(mdp.P[a][s].dot(V[k]))
10            star[k+1][s] = (np.argmax(X[k+1,:,s]))
11            V[k+1][s] = np.max(X[k+1,:,s])
12        if (np.max(V[k+1]-V[k])-np.min(V[k+1]-V[k])) < epsilon:
13            V[k+1:] = V[k+1]
14            star[k+1:] = star[k+1]
15            X[k+1:] = X[k+1]
16            break
17        else: pass
18    return star, V, X

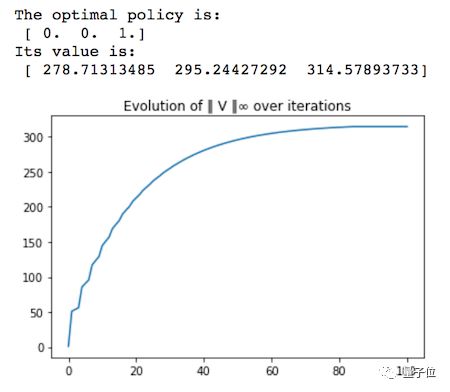
△ 奖励变化曲线

最优策略是等到森林处于古老且茂盛的状态时进行砍伐，这容易理解，因为在森林处于最古老的状态时砍伐的奖励是等待让森林生长的奖励的5倍，有r1=10，r2=50。

Q-Learning算法

Q-Learning算法中的“Q”代表着策略π的质量函数（Quality function），该函数能在观察状态s确定动作a后，把每个状态动作对 (s, a) 与总期望的折扣未来奖励进行映射。

Q-Learning算法属于model-free型，这意味着它不会对MDP动态知识进行建模，而是直接估计每个状态下每个动作的Q值。然后，通过在每个状态下选择具有最高Q值的动作，来绘制相应的策略。

如果智能体不断地访问所有状态动作对，则Q-Learning算法会收敛到最优Q函数[1]。

有关Q-Learning的其他细节，这里不再介绍，更多内容可观看Siraj Raval的解释视频。

   

下面我们给出关于Q-Learning算法的Python实现。

要注意，这里的学习率α是w=4/5时的多项式，这里使用了引用[3]的结果。

这里使用的ε-greedy搜索策略，后面会详细介绍。

 1def q_learning(mdp, num_episodes, T_max, epsilon=0.01):
 2    Q = np.zeros((mdp.S, mdp.A))
 3    episode_rewards = np.zeros(num_episodes)
 4    policy = np.ones(mdp.S)
 5    V = np.zeros((num_episodes, mdp.S))
 6    N = np.zeros((mdp.S, mdp.A))
 7    for i_episode in range(num_episodes): 
 8        # epsilon greedy exploration
 9        greedy_probs = epsilon_greedy_exploration(Q, epsilon, mdp.A)
10        state = np.random.choice(np.arange(mdp.S))
11        for t in range(T_max):
12            # epsilon greedy exploration
13            action_probs = greedy_probs(state)
14            action = np.random.choice(np.arange(len(action_probs)), p=action_probs)
15            next_state, reward = playtransition(mdp, state, action)
16            episode_rewards[i_episode] += reward
17            N[state, action] += 1
18            alpha = 1/(t+1)**0.8
19            best_next_action = np.argmax(Q[next_state])    
20            td_target = reward + mdp.discount * Q[next_state][best_next_action]
21            td_delta = td_target - Q[state][action]
22            Q[state][action] += alpha * td_delta
23            state = next_state
24        V[i_episode,:] = Q.max(axis=1)
25        policy = Q.argmax(axis=1)
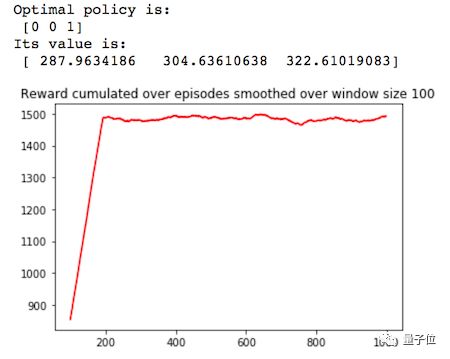
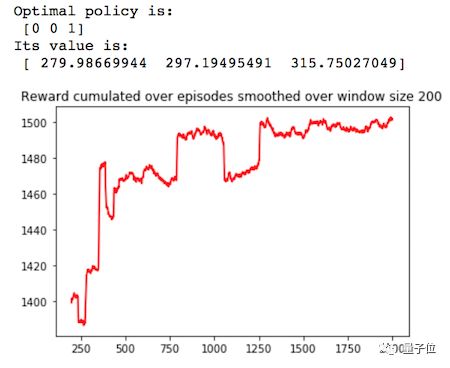
26    return V, policy, episode_rewards, N

△ 奖励变化曲线

探索与利用的平衡

序列学习算法会涉及到一个基本选择：

• 利用：根据当前信息做出最佳决策；

• 探索：做出其他决策来收集更多信息。

合理平衡好探索和利用的关系，对智能体的学习能力有重大影响。过多的探索会阻碍智能体最大限度地获得短期奖励，因为选择继续探索可能获得较低的环境奖励。另一方面，由于选择的利用动作可能不是最优的，因此靠不完全知识来利用环境会阻碍长期奖励的最大化。

ε-greedy搜索策略

该策略在每一步利用概率ε来选择随机动作。

这可能是最常用也是最简单的搜索策略，即用ε调整探索动作。在许多实现中，ε会随着时间不断衰减，但也有不少情况，ε会被设置为常数。

1def epsilon_greedy_exploration(Q, epsilon, num_actions):
2    def policy_exp(state):
3        probs = np.ones(num_actions, dtype=float) * epsilon / num_actions
4        best_action = np.argmax(Q[state])
5        probs[best_action] += (1.0 - epsilon)
6        return probs
7    return policy_exp

不确定优先搜索策略

不确定优先（Optimism in Face of Uncertainty）搜索策略，最开始被用来解决随机式多臂赌博机问题 （Stochastic Multi-Armed Bandit），这是一个很经典的决策问题，赌徒要转动一个拥有n个槽的老虎机，转动每个槽都有固定回报概率，目标是找到回报概率最高的槽并且不断地选择它来获取最高的回报。

赌徒面临着利用还是探索的问题，利用机器获得最高的平均奖励或探索其他未玩过的机器，以期望获得更高的奖励。

这个问题与Q-Learning算法中的探索问题非常相似：

• 利用：在给定状态下选择具有最高Q值的动作；

• 探索：做出其他决策来探索更多信息，通过选择不了解或不够了解的环境。

不确定优先状态：只要我们对某个槽的回报不确定时不确定手臂的结果，我们就会考虑当前环境来选择最佳的手臂。

不确定优先算法有两方面：

• 若当前处于最佳环境，那算法会直接选择最佳的手臂；

• 若当前不处于最佳环境，则算法会尽量降低不确定性。

置信区间上界（Upper Confidence Bound, UCB）是一种常用的不确定优先算法[2]，我们把它结合到Q-Learning方法中，有：

• Q(s, a)：状态s下动作a缩放后的Q值；

• N(t，s，a)：在时刻t和状态s下动作a被选择的次数。

此时，智能体的目标为Argmax {Q(s, a)/ a ∈ A}，这意味着在状态s中选择具有最高Q值的动作。但是在t时刻Q（s，a）值是未知的。

在t时刻，Q估计值为Q(t, s, a)，则有Q(s,a) =  + (Q(s,a) −  )。

(Q(s,a) −  )为相应误差项。

霍夫不等式 （Hoeffding’s inequality）可用来处理这类误差。事实上，当t变化时，有：

优先策略可写成：Argmax {Q+(t, s, a)/ a ∈ A}，且有：

当β大于0时，执行探索动作；当β为0时，仅利用已有估计。

这种界限方法是目前最常用的，基于这种界限后面也有许多改进工作，包括UCB-V，UCB*，KL-UCB，Bayes-UCB和BESA[4]等。

下面给出经典UCB算法的Python实现，及其在Q-Learning上的应用效果。

1def UCB_exploration(Q, num_actions, beta=1):
2    def UCB_exp(state, N, t):
3        probs = np.zeros(num_actions, dtype=float)
4        Q_ = Q[state,:]/max(Q[state,:]) + np.sqrt(beta*np.log(t+1)/(2*N[state]))
5        best_action = Q_.argmax()
6        probs[best_action] = 1
7        return probs
8    return UCB_exp

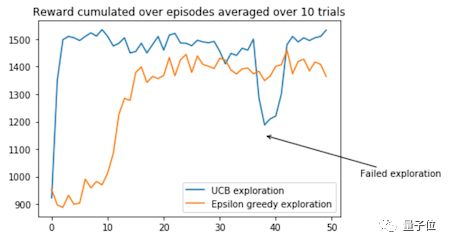
△ 奖励变化曲线

UCB搜索算法应该能很快地获得高额奖励，但是前期搜索对训练过程的影响较大，有希望用来解决更复杂的多臂赌博机问题，因为这种方法能帮助智能体跳出局部最优值。

下面是两种策略的对比图。

总结与展望

Q-Learning是强化学习中最常用的算法之一。在这篇文章中，我们讨论了搜索策略的重要性和如何用UCB搜索策略来替代经典的ε-greedy搜索算法。

更多更细致的优先策略可以被用到Q-Learning算法中，以平衡好利用和探索的关系。

参考文献

[1] T. Jaakkola, M. I. Jordan, and S. P. Singh, “On the convergence of stochastic iterative dynamic programming algorithms” Neural computation, vol. 6, no. 6, pp. 1185–1201, 1994.

[2] P. Auer, “Using Confidence Bounds for Exploitation-Exploration Trade-offs”, Journal of Machine Learning Research 3 397–422, 2002.

[3] E. Even-Dar, and Y. Mansour, “Learning Rates for Q-learning”, Journal of Machine Learning Research 5 1–25, 2003.

[4] A. Baransi, O.-A. Maillard, and S. Mannor, “Sub-sampling for multi-armed bandits”, Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 115–131, 2014.

原文：https://medium.com/sequential-learning/optimistic-q-learning-b9304d079e11

— 完 —

加入社群

量子位AI社群17群开始招募啦，欢迎对AI感兴趣的同学，加小助手微信qbitbot7入群；

此外，量子位专业细分群(自动驾驶、CV、NLP、机器学习等)正在招募，面向正在从事相关领域的工程师及研究人员。

进群请加小助手微信号qbitbot7，并务必备注相应群的关键词~通过审核后我们将邀请进群。（专业群审核较严，敬请谅解）

诚挚招聘

量子位正在招募编辑/记者，工作地点在北京中关村。期待有才气、有热情的同学加入我们！相关细节，请在量子位公众号(QbitAI)对话界面，回复“招聘”两个字。

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态