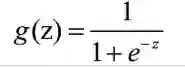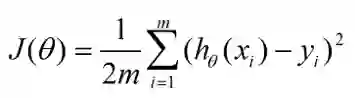逻辑回归算法背后的数学

逻辑回归算法背后的数学

看完Andrew Ng老师的机器学习公开课后，对于逻辑回归部分，打算写篇学习笔记记录总结一下，也和大家共同分享。

1

基本思能

逻辑回归（Logistic Regression）和线性回归（Linear Regression）的模型和原理是相似的（哈哈，给我的感觉就像是街霸游戏里的Ryu和Ken），按照我的理解，算法大致可以分为以下步骤：

（1）构造一个合适的预测函数，假设记为h函数。该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程非常关键，需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式（走势），比如是线性函数还是非线性函数。（例如y=x，y=x2，y=x3…… 等形式的函数）

（2）构造一个损失函数（loss function）并合成一个代价函数（cost function）。损失函数是表示每一个样本上，预测的输出h与训练数据类别（即真实值）y之间的偏差，可以是二者之间的差（h-y），也可以是（h-y）2（貌似这种常用一点，避免了可能出现负数的情况）或者是其他的形式。综合考虑所有训练数据的“损失”，将其求和或者求平均，就变成了代价函数，记为J(θ)函数（这里的参数θ是指预测函数里面的系数） 

（3）寻找代价函数最小值并确定参数。显然，我们希望J(θ)函数的值越小越好，因为这表示我们预测的和实际值越小了，预测函数的表现效果就越好，所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法，这里要提到的是梯度下降法（Gradient Descent），当然也有其他优秀的算法。

2

推导过程

1

 构造预测函数

逻辑回归是一种分类方法，用于两分类问题（即输出只有两种，表示为0和1）。根据上面步骤，需要先找到一个预测函数hθ(x)，在这里，我们假设是线性边界的情况，表示形式为：

因为逻辑回归的输出必须是两个值，所以要利用Logistic函数（或称为Sigmoid函数），把输出控制在0到1之间，函数形式为：

它的函数图像为：

结合这两个函数，我们可以得到：

好了，到了这里我们已经定义了一个预测函数，应当注意，hθ(x)的输出值的含义是：它表示结果取1的概率。

 

2

构造损失函数和代价函数

按照直观思想，或是参照线性回归的代价函数，我们可以写出以下的代价函数：

转自：算法与数学之美