生成对抗网络，10页pdf

2022 年 11 月 23 日 专知

生成对抗网络(GenerativeAdversarialNetwork,GAN)在诸多领域都取得了较好的应用效果,本章将以生成模型概述为切入点,介绍生成模型的基本概念和生成模型的意义及应用,在此基础上详细叙述 GAN,并分析 GAN 的延伸模型———SGAN 模型、CGAN 模型、 StackGAN 模型、InfoGAN 模型和 AuxiliaryClassifierGAN 模型的结构。

深度神经网络的热门话题是分类问题,即给定一幅图像,神经网络可以告知你它是什么内容,或者属于什么类别。近年来,生成模型成为深度神经网络新的热门话题,它想做的事情恰恰相反,即给定一个类别,神经网络可以无穷无尽地自动生成真实而多变的此类别图像,如图5.1所示,它可以包括各种角度,而且会在此过程中不断进步。

5.1.1 生成模型的基本概念

在深度学习中,可以将其模型分为生成模型和判别模型两大类[1]。生成模型可以通过观察数据,学习样本与标签的联合概率密度分布P(x,y),然后生成对应的条件概率分布P (y|x),从而得到所预测的模型Y=f(x)。判别模型强调直接从数据中学习决策函数[2]。生成模型的目标是给定训练数据,希望能获得与训练数据相同的新数据样本。判别模型的目标是找到训练数据的分布函数。在深度学习中,监督学习和非监督学习都包含其对应的生成模型,根据寻找分布函数的过程,可以把生成模型大致分为概率估计和样本生成。概率估计是在不了解事件概率分布的情况下,通过假设随机分布,观察数据确定真正的概率密度分布函数,此类模型也可定义为浅层生成模型,典型的模型有朴素贝叶斯、混合高斯模型和隐马尔可夫模型等。样本生成是在拥有训练样本数据的情况下,通过神经网络训练后的模型生成与训练集类似的样本,此类模型也可以定义为深度生成模型,典型的模型有受限玻尔兹曼机、深度信念网络、深度玻尔兹曼机和广义除噪自编码器等。

5.1.2 生成模型的意义及应用

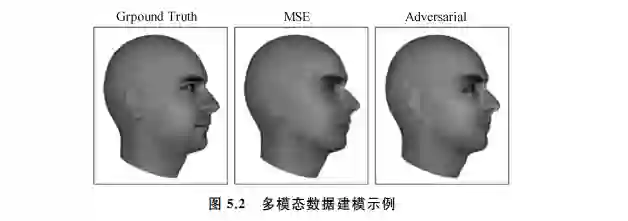
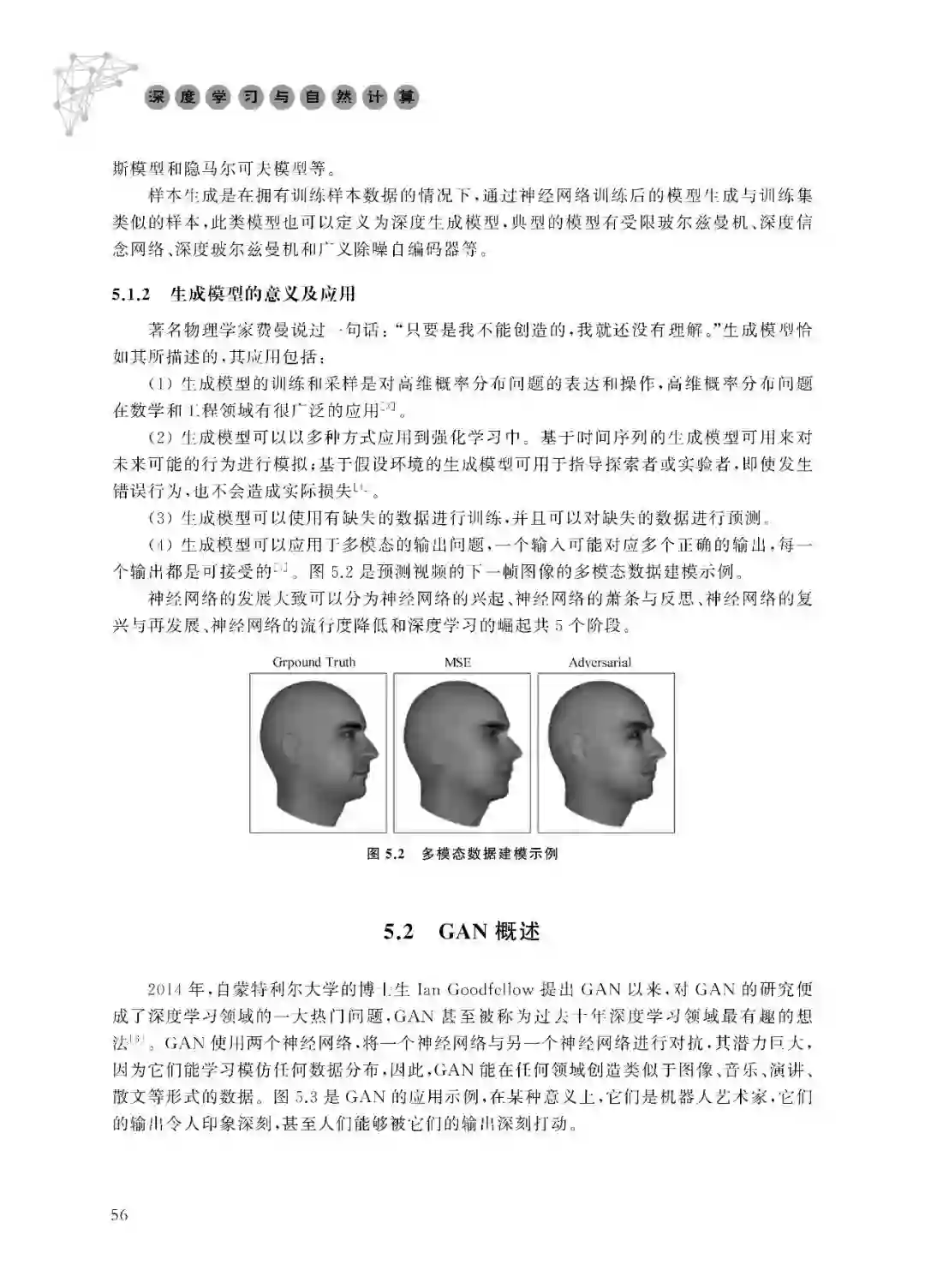
著名物理学家费曼说过一句话:“只要是我不能创造的,我就还没有理解。”生成模型恰如其所描述的,其应用包括: (1)生成模型的训练和采样是对高维概率分布问题的表达和操作,高维概率分布问题在数学和工程领域有很广泛的应用[3]。(2)生成模型可以以多种方式应用到强化学习中。基于时间序列的生成模型可用来对未来可能的行为进行模拟;基于假设环境的生成模型可用于指导探索者或实验者,即使发生错误行为,也不会造成实际损失[4]。(3)生成模型可以使用有缺失的数据进行训练,并且可以对缺失的数据进行预测。(4)生成模型可以应用于多模态的输出问题,一个输入可能对应多个正确的输出,每一个输出都是可接受的[5]。图5.2是预测视频的下一帧图像的多模态数据建模示例。神经网络的发展大致可以分为神经网络的兴起、神经网络的萧条与反思、神经网络的复兴与再发展、神经网络的流行度降低和深度学习的崛起共5个阶段。