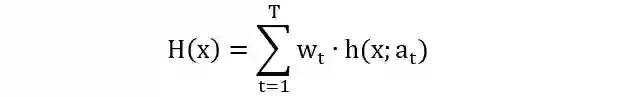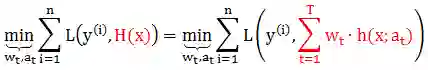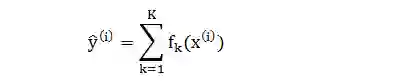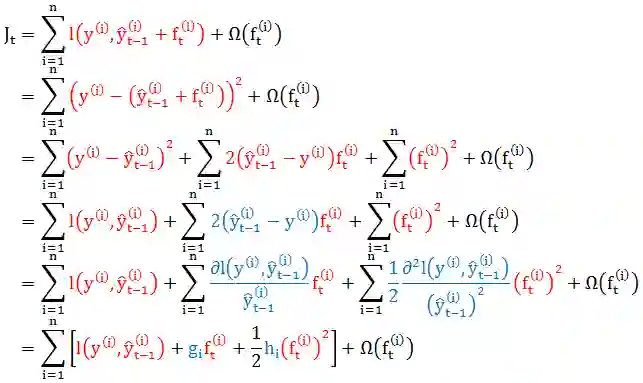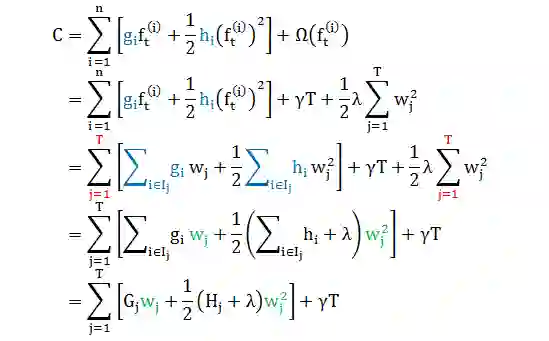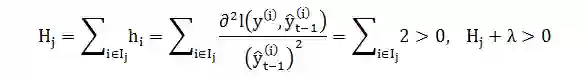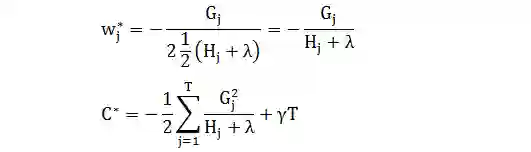极度梯度提升
有没有一种人很讨厌,比如在对两份工作做比较时,你和他道前景,他跟你讲技术;你和他讲技术,他跟你说薪水;你和他说薪水,他跟你谈情怀;你和他谈情怀,他又和你道前景。争论永远没有个头,而且你基本上对这两份工作做不了任何比较。
如果工作 A 不论从前景、技术、薪水和情怀都力压另一份工作 B,那么任何人都会选择工作 A 吧。在提升树 (boosted tree) 的世界里,也有这么一个完胜其它的“工作 A”,它就是大名鼎鼎的 XGBoost,全称 eXtreme Gradient Boost,翻译为极度梯度提升。顾名思义,XGBoost 本质上是一个梯度提升方法,但是作用在树上面,极度指的是把提升做到极致。
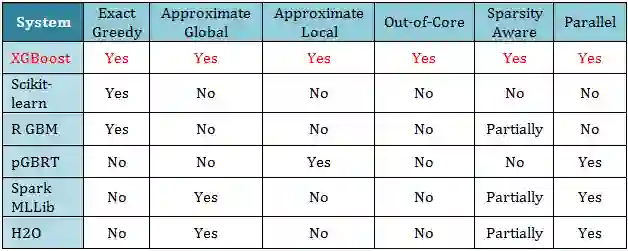
下图给出了 XGBoost 和其他开源系统方法的各项对比,发现 XGBoost 真的是完胜。
XGBoost 的实力图是不是很像下面的马龙六边形战力分析图?
马龙在力量、速度、技术、发球、防守和经验每项满分,战斗力图成完美的正六边形。再看看日本最强水谷隼的战斗力,虽然不错但是和马龙比还是有一定差距。
“我每项都是 5 分是因为上限只有 5 分” -- 马龙
要学就学最好的,要不就别学。
第一章 - 前戏王
1.1 回归分类树
1.2 树的重定义
1.3 树的复杂度
1.4 加法模型和前向分布算法
第二章 - 理论皇
2.1 XGBoost 简介
2.2 XGBoost 泛化度
2.3 XGBoost 精度
2.4 XGBoost 速度
第三章 - 实践狼
3.1 Allstate 数据集
3.2 Higgs Boson 数据集
3.3 Yahoo LTRC 数据集
3.4 Criteo 数据集
总结

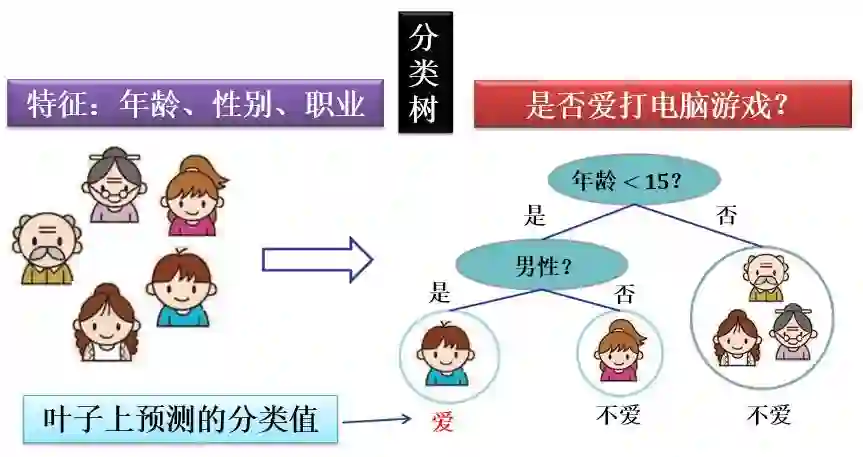
XGBoost 里面的树是分类回归树 (classification and regression tree, CART), 它既可以用于创建分类树 (classification tree),也可以用于创建回归树 (regression Tree)。CART 的主要特点有:
特征选择:根据 CART 要做回归还是分类任务,对于
回归树:用平方残差 (square of residual) 最小化准则来选择特征,叶子上是类别值
分类树:用基尼指数 (Gini index) 最小化准则来选择特征。叶子上是实数值
二叉树:在内节点都是对特征属性进行二分 (binary split)。根据特征属性是连续类型还是离散类型,对于
连续类型特征 X:X 是实数。可将 X < c 对应的样例分到左子树,X > c 对应的样例分到右子树,其中 c 是最优分界点,由最小化平方残差而得
离散类型特征 X :X 是 n 类变量。假设 n = 3,特征 X 的取值是好、一般、坏,那么二分序列会有如下 3 种可能性:
{ [好,一般],[坏] }
{ [好,坏], [一般] }
{ [好], [一般,坏] }
需要分别计算按照上述三个在二分序列做分叉时的基尼指数,然后选取产生最小的基尼指数的二分序列做该特征的分叉二值序列参与回归树。因此,CART 不适用于离散特征有多个取值的场景。
停止条件:根据特征属性是连续类型还是离散类型,对于
连续类型特征:当某个分支里所有样例都分到一边
离散类型特征:
当某个分支里所有样例都分到一边
当某个分支上特征已经用完了
对“停止条件”这条还想加点说明:根据离散特征分支划分子树时,子树中不应再包含该特征。比如用特征“相貌”来划分成左子树 (相貌=丑) 和右子树 (相貌=美),那么无论在哪颗子树再往下走,再按特征“相貌”划分完全时多余的,因为上面早已用“相貌”划分好;而根据连续特征分支时,各分支下的子树必须依旧包含该特征 (因为该连续特征再接下来的树分支过程中可能依旧起着决定性作用)。
通常先让 CART 长成一棵完整的树 (fully-grown tree),之后为了避免过拟合,再后修剪 (post-pruning) 树,具体用到的方法见决策树一贴。
下面两图画出单个分类树和回归树:
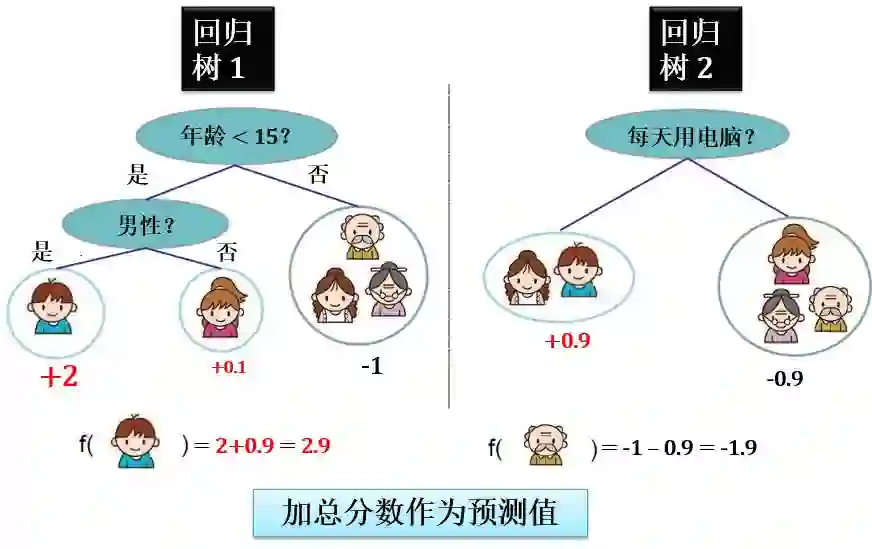
下面两图画出集成 (多个) 分类树和回归树:
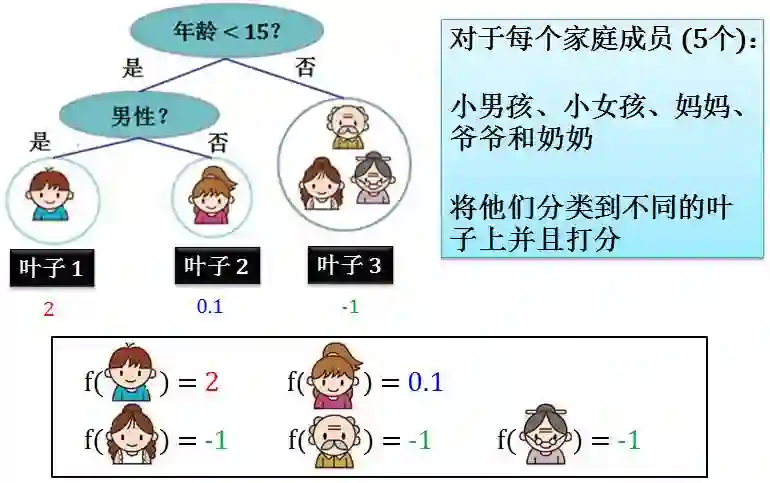
在上面用两棵回归树来预测的例子中。对于每个样本的预测结果就是每棵树预测分数的和。比如在是否爱打电脑游戏这个问题上
小男孩的得分为 2.9 分,2 和 0.9 之和
老爷爷的得分为 -1.9 分,-1 和 -0.9 之和
在上节讲的 CART 中,我们将家庭成员分类到不同的叶子里,然后根据对应的叶子而打分。
上图 f 是一个从家庭成员到得分的映射,有
f(家庭成员) = 分数
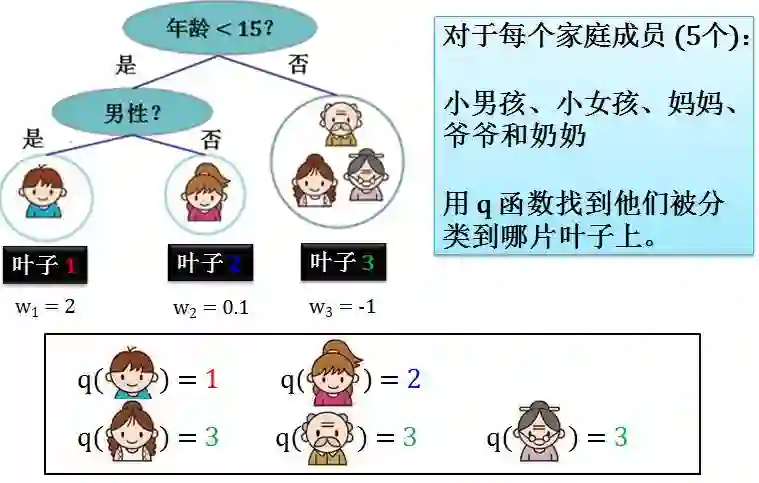
如果根据数据 (家庭成员) 从头到尾遍历一边,上面定义的树很方便。但是有的时候我们需要根据叶子从头到尾遍历一边,上面定义的的树就不是很方便,因此需要重新定义。
上述定义乍一看让人困惑,但是当你知道 T 是叶子的个数,d 是家庭成员的个数,一切都变得简单了。 其中
q(家庭成员) = 叶子的索引,根据 q 这个映射可以得到每个家庭成员被分配到哪片叶子
wq(x) 其实就是 w1 或者 w2 或者… 或者 wT
w 是个 T 维向量,因为每片叶子对应着一个分数
如果按照叶子索引来汇总每个数据上的函数值,我们需要定义一个从叶子索引到数据索引的映射
Ij= {i|q(x(i)) = j}
其中 x(i) 是第 i 个数据(家庭成员),i|q(x(i)) = j 是找到第 j 片叶子对应的家庭成员的索引,因为这样的 i 不止一个,因此 Ij 是一个集合。具体示例如下:
树的复杂度定义如下:
具体示例如下:
加法模型 (additive model) 是由一系列的基函数 (base function) 线性组成,表示如下
其中
h(x; at)是基函数
at 是基函数的参数
wt 是基函数的系数 (权重)
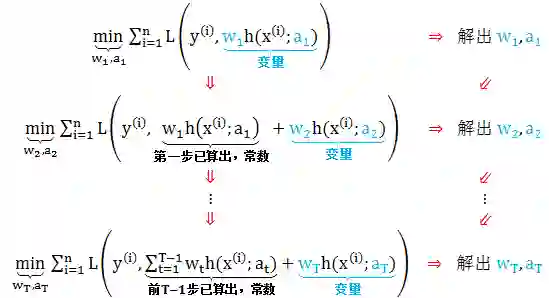
在给定训练数据 (x(i), y(i)) 及损失函数 L(y, H(x)) 的条件下,学习加法模型 H(x) 可转换成下面损失函数最小化问题
通常一次性优化解出 wt 和 at 是很复杂的,我们现在思路是如果从 t 等于 1 到 T,每一步只学习一个基函数和其系数,逐步逼近上面的函数式,从而简化了优化的复杂度。具体优化步骤如下:
上面的算法也称为前向分布 (forward stage-wise) 算法。
这样,前向分布算法将同时求解从 t 等于 1 到 T 所有参数 wt 和 at 的优化问题简化为逐步求解各个 wt 和 at 的优化问题。大家仔细回顾一下上贴集成学习前传讲的 adaBoost 算法里面也是逐步确定权重的,和前向分布算法的步骤很像,两者有什么联系吗?
从数学模型角度上来说,XGBoost 说白了是一个加强版的梯度提升树,可以用来做回归和分类。在我们讨论和举例中,只研究回归树。
和以往梯度提升树 (gradient boosted tree, GBT) 比起,XGBoost 的改进地方在:
提高泛化度 (正则项、缩减率、列抽样)
提高精确度 (二阶导)
提高速度 (算法优化、系统优化)
首先明确本贴需要用到的数学符号
XGBoost 方法集成 K 棵树得到的预测结果为
在了解 XGBoost 模型之前,强烈建议先读一遍“随机森林和提升树”一贴里的梯度提升树那部分。
XGBoost 比传统 GBT 的泛化能力 (generalization) 好,是因为前者用了三个防止过拟合 (overfitting) 的技巧:
在代价函数中加入正则项 (regularized term)
在加法模型里加入缩减率 (shrinkage)
在集成森林时加入列抽样 (column sub-sampling)
正则项
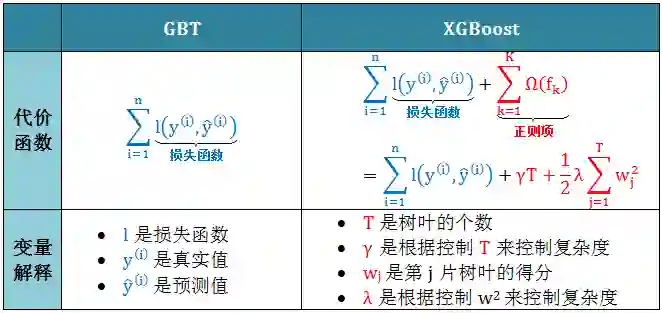
XGBoost 在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了
树的叶子节点个数 T
每个叶子节点上输出的得分的平方和 w2
下表对比 GBT 和 XGBoost 的代价函数
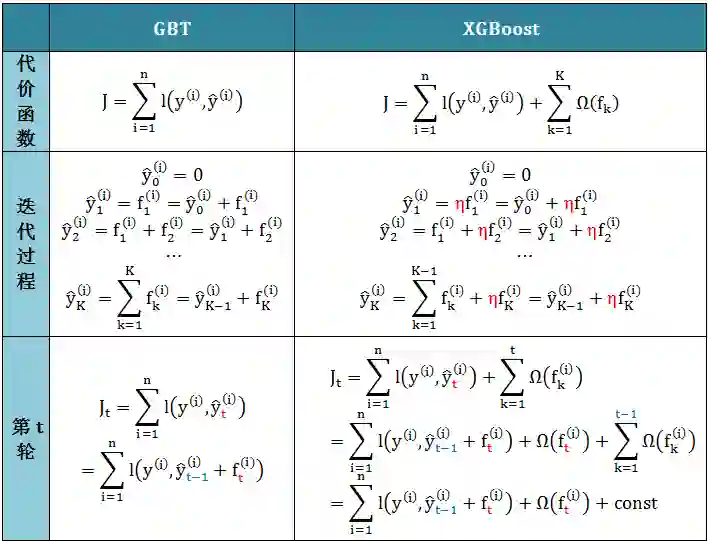
从偏差方差权衡 (bias-variance trade off) 的角度来讲,正则项降低了模型的方差,使学习出来的模型更加简单,防止过拟合,这也是 XGBoost 优于传统 GBT 的一个特性。 和 GBT 一样,XGBoost 也是通过加法模型和前向分布算法来训练模型的,类比如下
加法模型的核心就是开始给定一个常数初始值,每步都添加一个新的函数 fk。这个函数形式如何决定呢?将函数 f 当成 J 的变量,求导解出。
缩减率
缩减率相当于梯度下降里的学习率 (learning rate)。XGBoost 在进行完一次迭代后,会将新加的树模型乘上它 (上表红色的 η),主要是为了削弱每棵树的影响,让后面有更大的学习空间。在实际操作中,η 通常设为 0.1,当然也可以通过调参数得到。
列抽样
列抽样是 XGBoost 了随机森林的做法。因为树可以在特征集上分裂,因此在每棵树不同分裂点上,从 m 个特征中随机选择 j 个 (j < m) 而规定这个分裂点上只能在这 j 个特征上做分裂。这样做不仅能降低过拟合,还能减少计算量。在实际操作中,通常会给一个百分比 a,即 a%×m 的特征每次被选中用于分裂。
传统 GBT 在优化时只用到一阶导数信息,XGBoost 则对代价函数 Jt 进行了二阶泰勒展开 (忽略常数项),同时用到了一阶和二阶导数。以平方损失函数 l = (y-y^)2 为例
上面证明从“损失函数是平方形式的特殊情况”泛化成“任何损失函数的一般情况”,对第 i 个数据来说,gi 和 hi 是损失函数 l 对“第 t-1 轮的预测值”的一阶导和二阶导。
在求解 gi 和 hi 时按照叶子整合 (而不是按照数据整合) 更简单些,接着上面的推导 (将 J 看成是 f 的函数,因此l可看成常数项而拿掉),根据小节1.3 里面 f(x) 和 q(x) 的定义
上面推导
第二行带入复杂度函数形式
第三行用 w 代替 f,并在叶子上(而不是在数据上) 求和
第四行合并项,发现 C 是 T 个独立 wj 的二项函数的和
第五行定义 Gj 和 Hj 而化简
当损失函数是平方函数时,
因此 C 是开口向上的二项函数,有最小值:
不好理解?上图举例
XGBoost 厉害的是,模型使用者可以任意定义目标函数,只要它能出其一阶二阶导数即可。
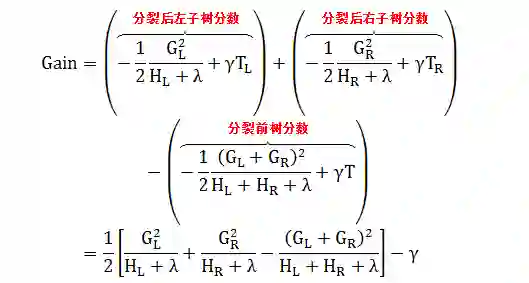
回忆决策树一帖,构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个结点处按照某一特征属性的不同值构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。
而在 XGBoost 里面定义的树的结构 q,上节公式 C* 可看成一个打分函数,类似于决策树里测量测度的指标 (分类误差率、信息增益、信息增益比、基尼指数等)。
从一片叶子开始,定义
IL 和 IR 是分裂后左右子树节点的集合
I 是分裂前树节点的集合,I = IL + IR
TL 和 TR 是分裂后左右子树叶子的个数
T 是分裂前树叶子的个数,T = TL + TR – 1
则分裂之后的获益 (gain) 为
和决策树分裂过程类似,XGBoost 有自己的确定贪心算法 (exact greedy algorithm)。
该算法需要主要的地方是步骤 2 里面将特征值 xk(j) 先排序,再扫描得到最优切分点。下图展示如何根据特征“年龄”来切分。
家庭成员有 5 个,每个都有自己的年龄,一共有 5 个年龄。将其按大小排序,算出两两平均值,有 4 个分别记为 a1, a2, a3 和 a4。按照每个 a 分裂算出 Gain,找到最大值对应的作为分裂点。
XGBoost 除了前面在泛化度和精确度做了特殊处理,在速度上也下了很大的功夫,比如在算法优化和系统优化上。
在算法优化 (algorithmic optimization) 上,XGBoost 主要加了以下两种技巧:
加权分位数草图:处理近似树学习中的实例权重。
稀疏感知算法:用于处理稀疏数据。
加权分位数草图
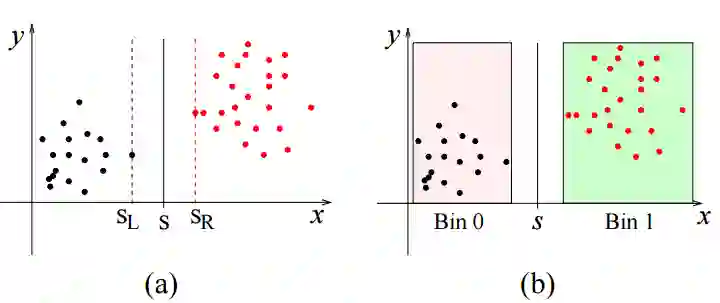
贪心算法很强大,因为它枚举出所有特征来选取分裂点,但是这样做效率很低,因此我们用近似算法 (approximate algorithm) 来改进。
在提升树模型中,单个树是被认为没有什么预测能力的,因此我们可以很粗糙的构建它,比如从分裂特征的做法上。如下图,x 代表特征值,y 代表误差。由图 (a) 可看出,分裂点 s 在 [sL, sR] 区间变都不会影响分裂带来的误差。
而图 (b) 将多个黑点和红点装成不同的箱 (bin),把它们当成一个个体,比如 Bin 0 就是一个数据,Bin 1 就是一个数据。因为这么做,分割点 s 在 Bin 0 和 Bin 1 中间动来动去都不会影响分裂带来的误差。
而近似算法先通过特征分布的分位数 (quantile) 获得候选分割点 (candidate split points) 的分布情况,然后根据候选分割点将连续的特征值映射到不同的箱中,最后统计汇总信息。
XGBoost 用的近似算法叫做加权分位数草图 (weighted quantile sketch),理论证明非常复杂,但说白了也就是一种找候选分割点的方法,只不过考虑到了权重。
下表列出如何找第 k 个特征的候选分割点。
现在有三个疑问:
ε 含义是什么?
为何此算法出现了两阶导 h?
r 含义是什么?
答:
ε 是什么不好说,但 1/ε 是候选点的数量,如果 ε = 0.1,那么对应着箱子里应该有 10 个候选点,更准确地说,10 个加权候选点。
h 实际是权重,配方一下 C 的表达式即可看出 h 处在权重的位置
r 其实计算的是一个关于 h 的分数 (当 x 小于某个值 s ),分母是所有 h 的和,分子是当 x 小于 s 时 h 的和。假如 D = {(1,1),(2,2), (3,3)},那么当
s = 1.5,r(1.5) = 1/(1+2+3) = 1/6,
s = 2.7,r(2.7) = (1+2)/(1+2+3) = 1/2
s = 3.2,r(3.2) = (1+2+3)/(1+2+3) = 1
需要强调的是,该近似算法有全局 (global) 和局部 (local) 两种类型:
全局近似算法是在建树之前先找好候选分割点,并且在各层分裂时都用它。
局部近似算法是在建树中 (每次分裂) 找候选分割点。
很明显,全局近似算法只需找一次候选分割点,但是为了达到和局部近似算法类似的表现,需要更多的候选分割点。这个结果在第 3.2 小节展示。
最后,下表给出近似算法:
稀疏感知算法
在实际问题中,数据很有可能是稀疏 (sparse) 的,原因有三:
数据有缺失值 (missing value)
数据包含很多 0
分类变量经过独热编码 (one-hot encoding) 得到很多 0
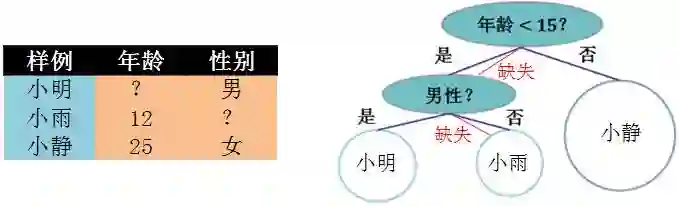
对缺失值的处理。对于特征的值有缺失的样本,XGBoost 可以自动学习出它的分裂方向。如下图例子:
在用年龄分裂时,小明的年龄不详,按照某种规则被分到小于 15 岁;接下来在用性别分裂时,小雨的性别不详,按照某种规则被分到女性。这些规则都是从数据中学来的,比如将小明分到小于 15 岁和大于等于 15 岁,看哪个分类误差小就选哪个。
稀疏感知算法 (sparse-aware algorithm) 将上面三种情况里的缺失值 (包括独热编码的一大堆 0) 自动根据数据学出最优分裂。
第 3.1 小节会展示采取和不采取稀疏感知算法的用时比较。
在系统优化 (system optimization) 上,XGBoost 主要加了以下三种技巧:
并行化:用所有 CPU 内核并行训练树
缓存优化:利用硬件优化数据结构和算法
核心外计算:计算超过内存大型数据集
并行化
XGBoost 工具支持并行 (parallelization)。但是提升树不是一种串行的结构吗?根据加法模型,第 t 次迭代的代价函数里包含了前面 t-1 次迭代的预测值,是一次迭代完才能进行下一次迭代的,怎么能并行呢?
每一棵树都要按顺序生成出来啊。但是注意 XGBoost 的并行不是按照树的粒度并行的,而是按照特征的粒度来并行的。首先我们来看看分裂过程的伪代码:
接下来我们看看如何并行化上面伪代码描述的步骤。
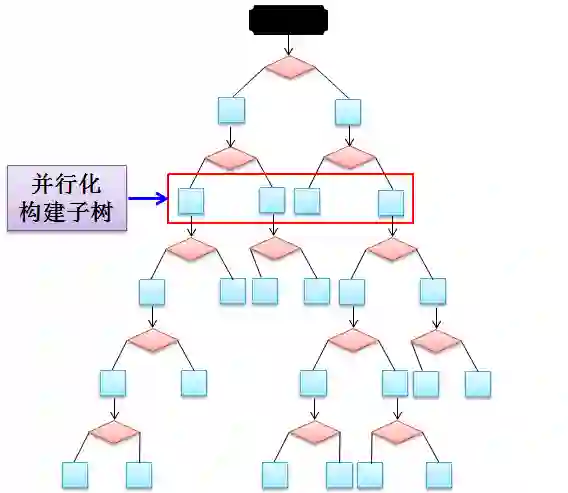
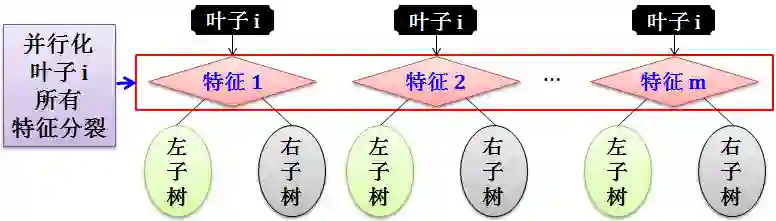
第一种:并行化子树构建
如上图所示,以红框那层 4 片叶子举例,我们并行化构建子树过程。但是这种并行方式有严重的问题,就是工作量失衡 (workload imbalanced)。比如第二和三片的叶子含有的样例就明显小于第一和四片的叶子含有的样例。这样会造成并行时的工作量不均衡,因而并行效率也不高。直接并行构建子树太粗了,我们需要一种更细分的并行化。
第二种:并行计算某片叶子的所有特征分裂值
在某片叶子要进行分裂时,对 m 个特征进行并行化计算出最佳分裂值 S,比较所有 S 选出最佳中的最佳。
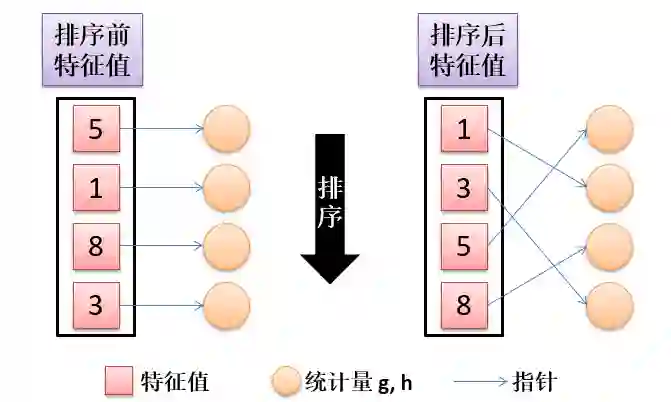
从小节 3.2 的算法 2 可知,在树分裂前每个特征的特征值都需要排序,而这个步骤是非常耗时的。为了减低排序用时,可将数据存在存储单元 (in-memory unit),又叫块 (block)。在每块中,数据是以压缩柱 (compressed column) 形式存储;而在每个柱状中,数据按特征值大小来排序。
在贪心算法中,我们将整个数据集存储在一个单块 (single block) 中,对每个特征按其特征值排序,如下图所示:
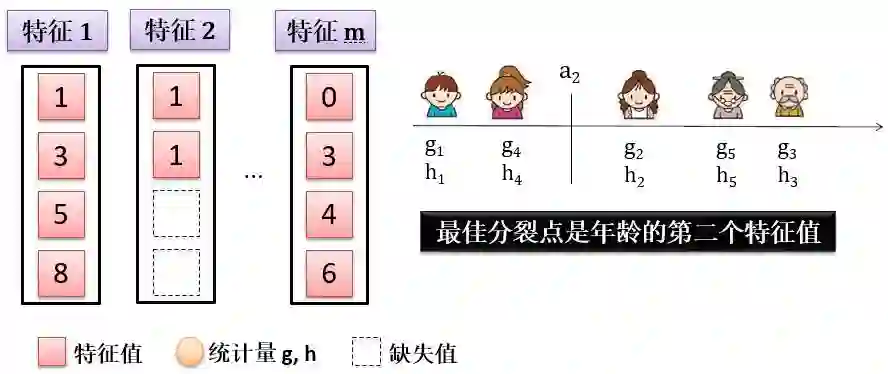
然后根据每个特征的已排序好的特征值进行线性扫描 (linear scan),如下图所示:
上图将 m 个特征的特征值排序,虚线框代表确实数据不参与排序。经过线性扫描得到年龄里的第二个的特征值 a2 是最佳分裂点。
这种并行方式比第一种好,但当树越来越深时,每片叶子包含的样例会越来越少,这种并行化带来的优势也越来越小。
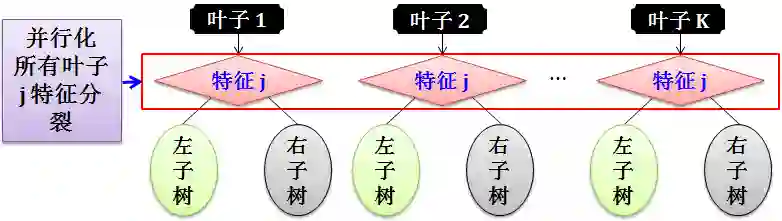
第三种:并行计算所有叶子的某个特征分裂值
在这种并行方式中,预先对每个特征进行了排序,后面的迭代中重复地使用这个排序,大大减小计算量。个人觉得这种并行方法比 XGBoost 的并行方法更高效。
缓存优化
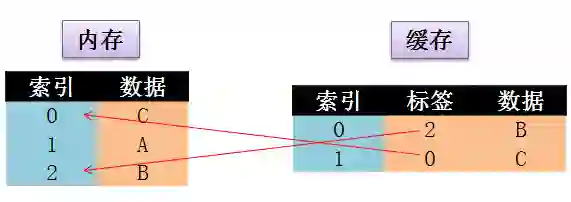
缓存 (cache) 是内存 (main memory) 中少部分数据的复制品。它们之间的联系如下图:
当某一硬件要读取数据时,会首先从缓存中查找需要的数据:
如果找到了则直接执行,称为 cache hit
如果找不到的话则从内存中找,成为 cache miss
由于缓存的运行速度比内存快得多,故缓存的作用就是帮助硬件更快地运行。
在 2.3 节讲到的 XGBoost 算法需要收集每个数据对应的 g 和 h,但是在排序之后,顺着行索引来获取的 g 和 h 不在连续的存储上,如下图:
指针 1 指向第二个圆圈,指针 2 指向第四个圆圈,指针 3 向第一个圆圈,指针 4 指向第三个圆圈,指针指向圆圈代表连续的存储访问。从上图看很明显顺着指针指的存储是不连续的。
第 3.2 小节会展示用缓存优化和不用缓存优化核在贪心算法和近似算法的表现。
核心外计算
XGBoost 还会充分利用计算机的资源实现可扩展 (scalable) 学习。除了处理器和内存,使用磁盘空间处理内存处理不了的数据能提高效率。启用外核计算 (out-of-core computing),我们将数据分成多个块,将每个块存储在磁盘上。在计算过程中,使用一个独立的线程来预取块主存储器,所以计算和磁盘读取可以同时发生。但是,这并不完全解决问题,因为磁盘阅读需要大部分的计算时间。减少开销很重要并增加磁盘输入输出 (IO) 的吞吐量 (throughput)。主要有两个改进核心外计算的技术:
块压缩 (Block Compression):每个块按列来压缩,在加载入内存时用一个独立线程随手解压缩。解压缩虽然用了一些时间,但是节省了磁盘读取成本。
块分片 (Block Sharding):分割数据到多个磁盘上。预取线程 (pre-fetcher thread) 分配给每个磁盘并将数据读取到内存缓冲区 (buffer),然后训练线程可选从每个缓冲区读取数据。如果有多个磁盘,那么绝对可以增加磁盘读取的吞吐量。
第 3.4 小节会展示采取和不采取外核计算的用时比较。
从业务角度来看,最重要的是端到端性能评估 (end-to-end performance evaluation)。公司高官层和客户都不会对训练误差,参数调整,模型选择等感兴趣。最重要的是在最终模型的 KPI。
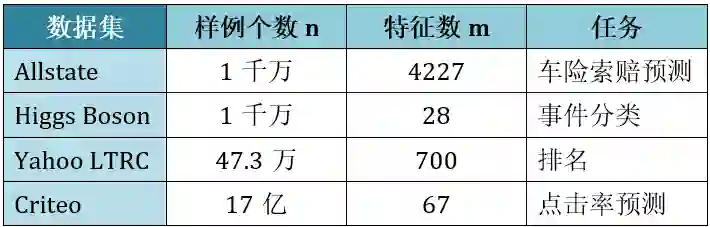
在本章中,4 个数据集被选中,其样例个数、特征数和任务总结在下表:
想查看 4 份数据详情,可在复制粘贴以下链接:
https://www.kaggle.com/c/ClaimPredictionChallenge/data
https://archive.ics.uci.edu/ml/datasets/HIGGS
https://webscope.sandbox.yahoo.com/catalog.php?datatype=c
http://labs.criteo.com/2013/12/download-terabyte-click-logs/
评估很难用单一指标 (single metric) 来完成。在评估中,主要是对比
在“相同线程不同数据量”下运行的时间和得分
在“不同线程相同数据量”下运行的时间和得分
接下来从这四份数据多角度展示 XGBoost 端到端的评估和完虐其他开源系统的表现。
注:用“D-X”形式表示用了 D 数据集里面的 X 个数据。
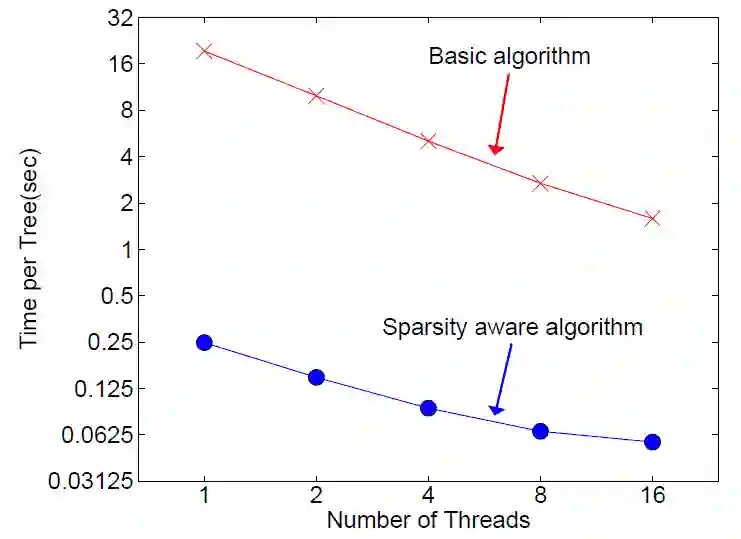
Allstate 是一套关于车保的数据,y 是保险金额,x 包括家庭 ID、车牌、车担保年份、型号等等。用 Allstate 数据集画出了在稀疏算法和缓存优化上的表现。
Allstate-10K: 稀疏算法
该数据几乎都是分类型变量,其实用独热编码转化后有大量的 0,非常稀疏。从上图可看出,用稀疏算法比没有稀疏算法可提速 50 倍。
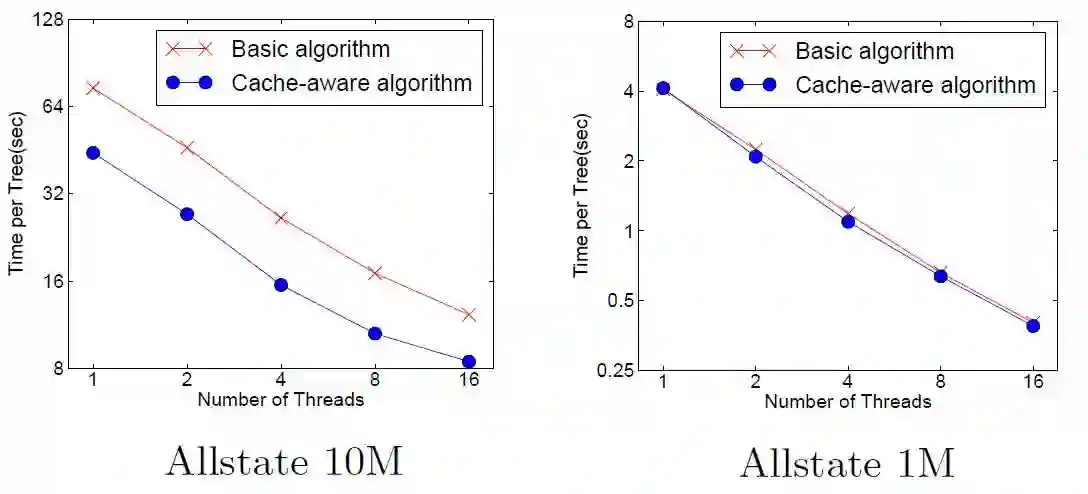
Allstate-1M, 10M: 贪心算法时缓存优化
在贪心算法下:
当数据量不大 (1M) 时,缓存优化对提速没有什么帮助 (右图)
当数据量大 (10M) 时,用缓存优化可提速 2 倍 (左图)
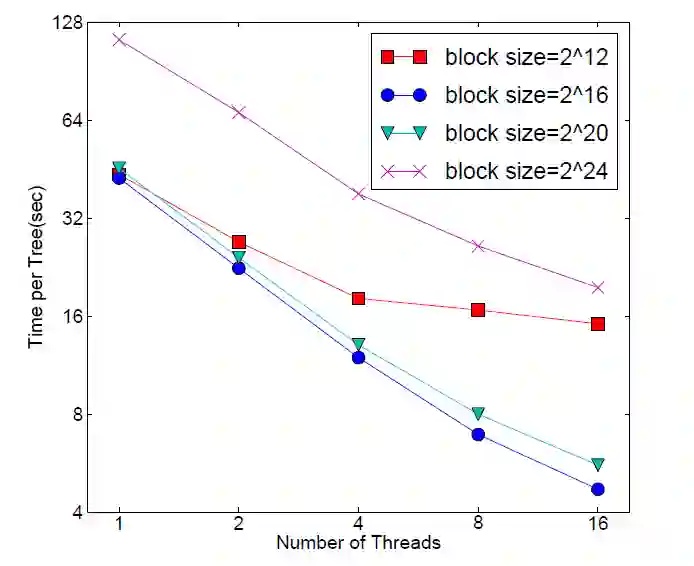
Allstate-10M: 近似算法时缓存优化
在近似算法的缓存优化中,我们需要找到一个块里的最优数据数量 (block size),如果数据量太小,在并行化时效率不高,如果数据量太大,很容易照成 cache miss。从上图可看出,最优 block size 是 216(蓝色圆形)。
Higgs Boson 是一套关于高能运动的数据,y 是类标签 (0 代表 signal, 1 代表 background),x 包括 21 个低级动作特征和 7 类高级动作特征。用 Higgs 数据集画出了在分裂算法和分类上的表现,但由于 Higgs 和 Allstate 在缓存优化的图和结论非常类似,我们就不重复描述。
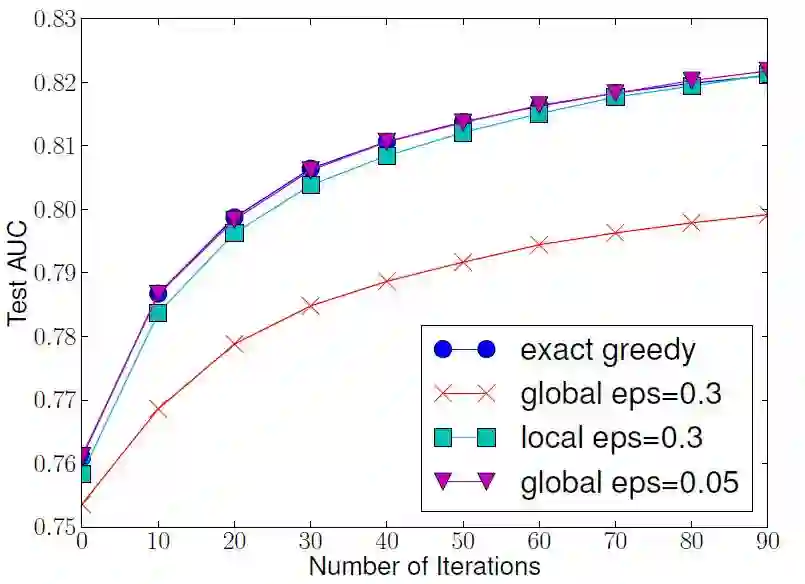
Higgs-10M: 分裂算法
以贪心算法的结果当成基准 (benchmark),我们发现全局法 (紫色倒三角) 和局部法 (青色正方形) 都可以达到同样 AUC 值,但是全局法付出了代价大些,0.05 的 ε 小于局部法 0.3 的 ε,这意味着全局法需要更多候选点的数量 (更大的 1/ε)。
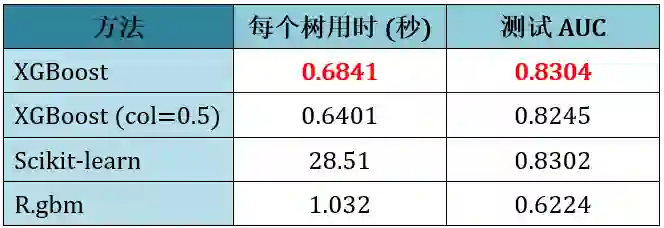
Higgs-1M: 分类 (500 棵树)
首先强调用 1M 个数据是为了让 scikit-learn 能在合理的时间段跑完出结果。从上表可得出:
XGBoost 和 scikit-learn 得到的 AUC 比 R.gbm 的好
XGBoost 比 scikit-learn 快 40 倍
XGBoost 列取样一半时表现比全取样稍差,速度略快
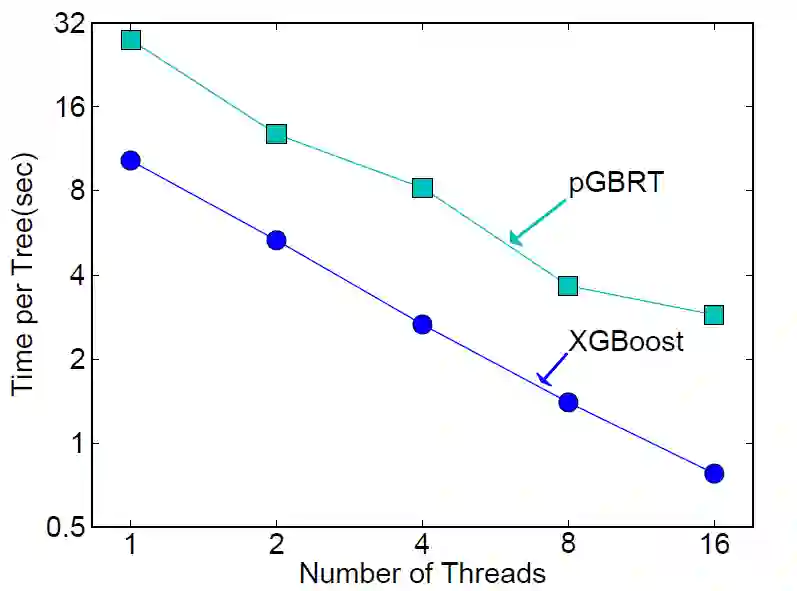
Yahoo LTRC 的关于网络搜索查询的数据,每条查询包含 22 个文本。
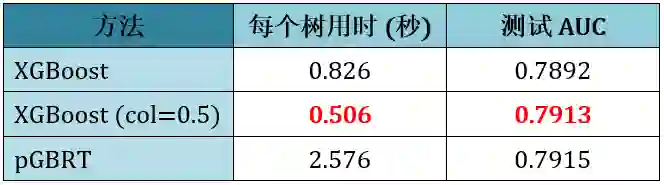
Yahoo LTRC: 排序(500 棵树)
从上表可得出:
XGBoost 比 pGBRT (业界做排序最强) 得到的 AUC 稍差一些,但是前者速度是后者速度 3 倍
XGBoost 列取样一半时和 pGBRT 的 AUC 几乎一样,但是前者速度是后者速度 5 倍
下图也清楚看到在不同线程情况下,XGBoost 都比 pGBRT 运行速度快。
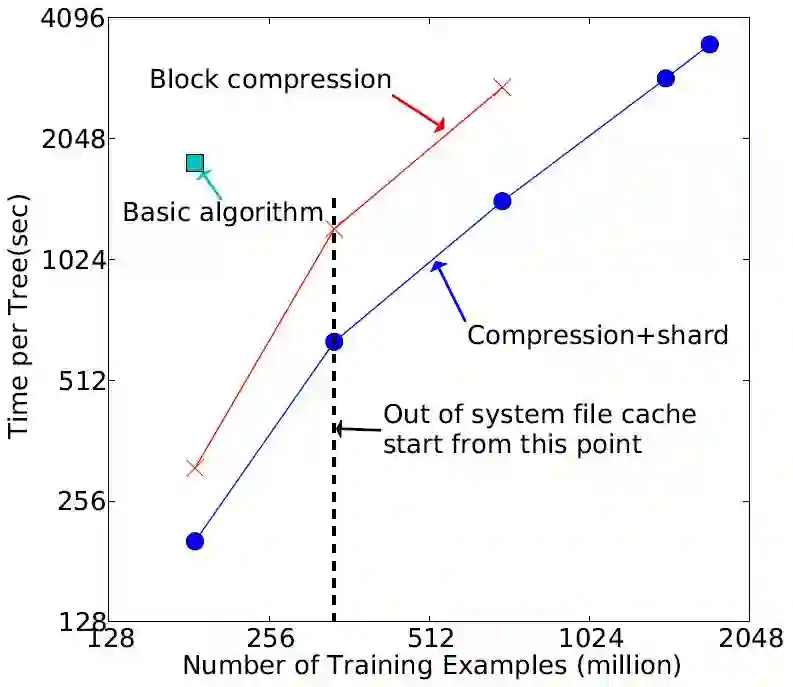
Criteo 的关于点击率 TB 级别的大数据,y 是点击率,x 包括 7 个整数特征和 26 个关于用户和广告等的特征。用 Criteo 数据集画出了在核外运算和分布式计算上的表现。
Criteo-1.7B: 核外运算
由上图可知:
只用块压缩可以加速 6 倍,用块压缩和块分片可以加速 12 倍
当系统没有多余的文件缓存时,用核外算法还是可以继续跑,只用块压缩最多只能跑到 700M 多个数据,而块压缩和块分片都用可以跑到 1.7B 个数据
Criteo-1.7B: 分布式计算
在本实验中我们比较 XGBoost 和两大能处理大数据的分布式系统 Spark MLLib 和 H2O。比较结果如下图:
左图是一个端到端的包括加载数据的耗时图,而右图一个不包括加载数据的每循环的耗时图,由上面两图可知:
H2O 加载数据很慢 (左图),因此用在端对端上效果会很差
当内存不足时,Spark MLLib 的速度会剧减 (斜率突然变高)
H2O大概只能运行到 350M 多个数据,Spark MLLib 大概只能运行到 700M 多个数据,但是 XGBoost 可以运行到 1.7B 个数据
XGBoost 代表 eXtreme Gradient Boosting,是一种可扩展 (scalable) 的树状升级系统。XGBoost 的可扩展性表现在几个重要的系统和算法优化上:
系统优化 (System Optimization)
并行化 (Parallelization):使用所有 CPU 内核并行训练树。
缓存优化 (Cache Optimization):利用硬件来优化数据结构和算法。
核心外计算 (Out-of-Core Computing):计算超过内存大型数据集。
算法优化 (Algorithmic Optimization)
加权分位数草图 (Weighted Quantile Sketch):处理近似树学习中的实例权重。
稀疏感知算法 (Sparsity Aware Algorithm):处理稀疏数据。
此外和以往梯度提升树比起,XGBoost的改进地方在:
高泛化度 (正则项、缩减率、列抽样)
高精确度 (二阶导)
高速度 (算法优化、系统优化)
XGBoost 是不是听起来无敌了,它是 Kaggle 竞赛者喜欢用的方法。的确
有了乔丹,谁还要詹姆斯
有了马龙,谁还要张继科
本帖基本把 XGBoost 的原理弄清楚了。下贴是实战贴,介绍如何用 python 里面 xgboost 包建模以及调参数。Stay Tuned!