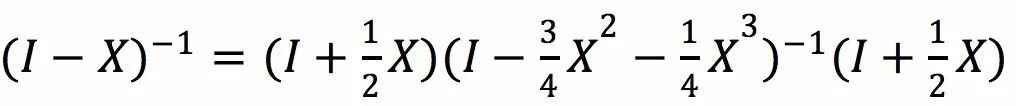二十一世纪计算 | 大数据和网络分析的可扩展算法

2017 年 11 月 8 日 微软研究院AI头条 21CCC

编者按：身处大数据时代，我们对高效算法的需求比先前任何时候都要突出。虽然大数据使我们进入了我们先驱者设想的渐近世界，但问题规模的爆炸式增长也对经典算法的有效性提出挑战：根据多项式时间表征，以前被认为有效的算法可能不再适用，有效的算法应该是可扩展的。

本文中，南加州大学计算机科学与数学系教授滕尚华展开讨论了一系列算法技术，用于在当今海量数据的世界中设计出可靠的可扩展算法。

南加州大学计算机科学与数学系教授滕尚华

（以下为滕尚华教授分享的精简版文字整理）

60年代，计算机逐渐成为独立的科学，最早从事计算机理论方面研究的先驱者们就开始考虑用渐进复杂度框架来研究算法问题，引进了许多现在已经非常普及的概念，比如大O和大Omega，尽管当时并不受大众欢迎。当时，大家总是在想今后的问题可能会逐渐变大、变复杂，届时如何用算法去刻画这类问题的复杂性成为了众多科学家的研究重点。

现在，我们进入了丰富多彩的数据世界，进入了海量数据、大规模网络、机器学习的时代。问题的大小已经产生了数量级的变化，如果用当时的多项式时间作为标准的话，原先很多很好的算法放到今天很有可能成为瓶颈，因此算法和其复杂性的设计也应该与时俱进。我们现在必须要寻求一种非常接近线性时间的算法，能够和问题大小一起增长的算法，这就是所说的“算法的可扩展性”，定义为算法渐进复杂度和数据大小的比值。所以我个人认为现在的可扩展性已经不是要求多项式时间了。可扩展性希望算法的渐进时间复杂度随数据的大小可以很慢地增长，比如两者比值为常数或者对数级别的。如果一个问题可以被可扩展地解决，那么这个比值需要很小，当问题规模逐渐变大时，这个算法也依然高效。

在当今海量数据的世界里，设计更快的算法是非常必要的，无论是机器学习或是数据分析都需要更多、更系统地去发展这些非常迅速的算法。所以怎么样才能创造出迅速的算法呢？我们需要先找到系统的方法，然后找到一种系统的转变，即如何把一个问题转变成另外一个问题。而这些可以通过多项式时间完成，由此我们可以设计出很多不同的算法。

Software Engineering的创始人Barry Boehm有一次在跟我开玩笑说，做理论和做实践的过程是没什么实际区别的：当你在做一个很快的算法，就相当于写一个可以被重用的软件，做出来以后人们就可以一直用它。这个观念实际上就是我们讲的归约，你怎么能够把一类问题归约到更加基本的一些问题上。如果这些基本的问题有解法的话，你的新的问题就会有解法。

我以一个很简单的图论问题为例给大家介绍一下。这是一个简单的图论和数据计算交叉的问题，前人还没有能够解决掉。我们希望能够解一个线性方程，你给一个矩阵和一个向量，要解一组方程Ax=b。但是我们主要考虑其中有一类矩阵叫拉普拉斯矩阵，矩阵中的一个值对应图中一条边的权重的相反数，而矩阵对角线上的值为该点的边权之和。这类矩阵在很多问题中都被用到。这个问题看起来很简单，但是实际上多年来大家都没有找到接近线性的算法。十年前，我们用一系列的图论方法证明，这类问题基本上可以在线性时间里全部解出来。这个结果出来以后，又经过了八年研究，很快这个结果就变成线性的算法了。以前很复杂的算法，后来很多人一直对它进行更新，现在已经基本成为和排序一样快的一个算法。

很多人问我为什么我会考虑这个问题。实际上很有趣，我们在中学的时候都学过解电流，只要给一个电路和两个点的电压差，我们很快都可以解出来。我们看自己的算法是线性的，只要解的时候和题目画出来的电路图是同一个数量级的，从头一节一节算下来就基本没有问题。但是进入新的时代，新问题中的电的网络并不定是并联和串联，而是随便连的。机器学习就有很多类似这样的问题。我个人很有兴趣，这么基本的一个问题，以前我们没有一个线性时间的算法。当时我们也不知道怎么回答它的意义，但是我们终于把这个基本的问题做出来了。但你很快能想到，这个和机器学习、图论的问题都有关系。

比如说平面图，它可以被画在一个平面上，而使得不会有边相交。John Hopcroft和Tarjan有个很漂亮的结果，可以在线性时间内判定一个图是否为平面图。有个最漂亮的定理叫Tutte’s Embedding，数学界经常会讲到这个定理：任何一个平面图，你只要把一个面钉下来，然后让每一个点都走到它周围的点的平均的那个值，这个画法就是平面图。很多年前，人们并不知道怎么算的，只知道这么画下来就是平面图。但现在我们可以解这个线性方程以后，实际上解这个嵌入就是解两个拉普拉斯方程。这相当于你可以用物理方式得到平面嵌入的结果，而且在线性时间内。

微软研究院在做机器学习的时候，他们很快就考虑到这实际上是最早的机器学习的问题。如果我有一个网络，钉下来这些点就相当于你学习的标签，你给他一个标签，它希望能够找到一个函数，很平稳地去把这个图表示出来。所以很多基于网络的学习问题都可以转换成这一类问题，实际上就是在解Tutte’s Embedding的问题，这类问题用我们的算法可以线性时间解出来。

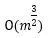
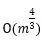
计算机有一个最大流问题，即给定一个网络，每条边上都有一些容量，你有一个出发点和结束点，要考虑的就是从出发点到结束点到底能够送多少的流量。这个问题和线性规划也非常相关。1975年这个问题最好的算法复杂度可以达到，之后一直没有发展过了。当我们的算法出来以后，我们第一次证明了，我们用电路图可以把这个问题复杂度减到。具体方法是，根据电流大小调整边上电阻大小。但是怎么样变大变小又是问题，实际上和一层的神经网络是一模一样的算法。没过几年大家已经把这个算法复杂度完全减少到可扩展了，所以这种最大流的算法已经可以做到在几乎线性的时间内完成。

大家越来越多用到电流去作为一个最基本的算法去改进很多很多以前很重要的算法。举一个很简单的例子，和现在的机器学习和计算问题有很大的关系。当我们在做大规模数据计算的时候，如何把数据变小是提升速度的关键所在，而稀疏化则能够有效解决问题。但是这个例子实际上只是一个特例，我们解电流时最主要的工作就是要证明所有的图都可以把它稀疏化，而且是可以在线性的时间实现稀疏化。所以我们当时解这个电流主要是在稀疏这个图。

在机器学习里有一个很重要的问题就是如何从一个分布里生成一个样本，这其中存在很多的随机变量，它们之间的关系非常复杂，而这种关系是用图表示出来的。从分布中生成样本一般被称作采样。机器学习领域中公认最简单的是用马尔科夫链。但是这样的做法往往很慢，所以实际中人们还是用采样的方法去做。当时有很多人在问如何能够线性拿到样本，这个机器学习中的存在的问题确实很困难。最后我们终于找到一个很简单的并行算法，而且基本上也是线性的。

这个问题可以变成一个数值计算问题。乍一看基本需要用三次方时间求解，别人会觉得这样很慢，我现在看有没有理论上的方式把它变快。实际上基本问题是解一个很简单的矩阵方程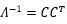，采样都不需要懂，唯一懂的就是这个基本问题，因为它可以从高斯采样问题中最终提炼得到。为了提升速度，我们问数学系这个问题怎么做。他们说这个很简单，因为矩阵是拉普拉斯矩阵，可以把它重新写一下。数学系给出的算法是最古老的牛顿算法，写出来是一个很简单的等式。具体涉及的公式是：

其中左右两个为线性的矩阵，中间为一个凸的线性组合。那个这个等式有什么用处呢？大家知道，牛顿算法是二阶收敛的，收敛非常迅速。中间的矩阵组合越来越接近I的，而且是以二阶的速度接近。那么为什么其他人不用牛顿算法算这些呢？因为用牛顿算法会让中间部分很快变得很稠密。数学家在用这个，实际没有人在用这个解问题。但我们在解电流过程中一直在做稀疏，当我看到这个问题时，我们能解决了，只需要把中间部分稀疏化就行。

所以，每次在考虑一个问题的时候，往往会出现越来越多的问题。所以，我们必须要把它逐渐解出来。

当我们做超快集的算法时，另外一种非常重要的方式叫网络局部探索。卷积神经网络实际上就是在做局部探索，我们可以把一个图先变成3×3分析，然后再变成2×2分析，这样一层一层这样分析下来，最后考虑怎么样能够把这些个局部探索很好地拼接起来，这可以帮助我们解决很多很复杂的问题。

我们举个很简单的例子，就是Google在对网页的重要性排序，就叫PageRank。PageRank的实际意义就是，当用户停留在某一个网页上时，随机走到下一个相邻网页中，其中偶尔会回到全局中其他点，最后求用户停留在这些网页上的分布。在回答网页搜索查询时，Google会拿这个PageRank值作为指标，但Google在回答问题时并不需要计算所有的网页PageRank值，它只需要关注显著的PageRank。比如它有一个阈值Δ，把所有PageRank值大于Δ的网页输出，反之去掉。这件事情最简单的算法是，通过局部探索对网页PageRank值做计算，经过几轮之后就能得到最终的值。问题是能否在O(n/Δ)的时间内把它算出来。这个量太大了，有平方级别的规模，但计算时不需要都算出来，可以通过局部近似得到。局部近似可以用常数时间把一行的PageRank值近似出来。最后需要解的问题是一个很简单的问题。具体是，给定一个向量，它的每个元素都是0和1之间的，然后求这一行的和是否大于Δ或者小于Δ的一半。当你能把这个简单问题做出来之后，你就能求出显著的PageRank值。