我不仅送100本纸质《统计学习方法》，连代码也都准备齐了

会员服务 ·

我不仅送100本纸质《统计学习方法》，连代码也都准备齐了

2019 年 7 月 22 日 七月在线实验室

各位同学，7月17日-23日为七月在线4周年庆典

将送出总价值远超6万的实物大奖!

并送出100本纸质技术书籍！

你没有看错

送100本！

100本！

↓↓↓↓↓

（上述书籍可任选1本）

想要吗？不过数量有限！

100本技术类纸质书，送完即止

↓立刻扫码进群，参与活动↓

↑扫他↑

李航的《统计学习方法》可以说是机器学习的入门宝典，许多互联网企业的面试、笔试题目，很多都参考这本书。

前段时间，黄海广博士在自己的 GitHub 上又更新了《统计学习方法》的 Python 代码，就迫不及待地分享给大家。

《统计学习方法》第一版还是 2012 年出版的，包含了众多主要的监督学习算法与模型。

2019 年 5 月 1 日，《统计学习方法》第二版正式发布，通过 6 年时间的努力，在第一版的基础上又增加了无监督学习的主要算法与模型。

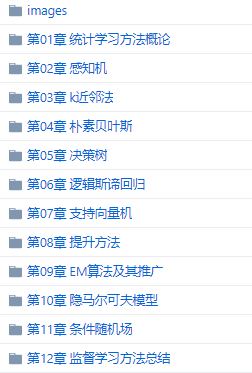
第二版的目录为：

第1篇监督掌习

第1章统计学习及监督学习概论
第2章感知机
第3章k近邻法
第4章朴素贝叶斯法
第5章决策树
第6章逻辑斯谛回归与优选熵模型
第7章支持向量机
第8章提升方法
第9章EM算法及其推广
第10章隐马尔可夫模型
第11章条件随机场
第12章监督学习方法总结
第2篇无监督学习
第13章无监督学习概论
第14章聚类方法
第15章奇异值分解
第16章主成分分析
第17章潜在语义分析
第18章概率潜在语义分析
第19章马尔可夫链蒙特卡罗法

第20章潜在狄利克雷分配

第21章 PageRank算法

第22章无监督学习方法总结

附录A 梯度下降法

附录B 牛顿法和拟牛顿法

附录C 拉格朗日对偶性

附录D 矩阵的基本子空间

附录E KL散度的定义和狄利克雷分布的性质

针对新增加的内容，黄海广博士对原有的 GitHub 源码进行新内容的更新，直接放上地址：

https://github.com/fengdu78/lihang-code

本次修改了部分错误，增加了每章概述，更新完前 12 章，今后将增加第二版的内容。

修改主要错误包括：

第3章 k近邻法的max_count错误
第10章隐马尔可夫模型的viterbi索引错误

增加的内容：

增加每章的概要

项目目前包含的内容截图如下：

目前，该项目已经收获 5000+ 的 star 了。

Python 代码

下面，以支持向量机为例，我们可以查阅 SVM 的完整示例代码：

class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel

    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0

        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0

    def _KKT(self, i):
        y_g = self._g(i) * self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1

    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
        return r

    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k] * x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1)**2

        return 0

    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]

    def _init_alpha(self):
        # 外层循环首先遍历所有满足0<a<C的样本点，检验是否满足KKT
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)

        for i in index_list:
            if self._KKT(i):
                continue

            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j

    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha

    def fit(self, features, labels):
        self.init_args(features, labels)

        for t in range(self.max_iter):
            # train
            i1, i2 = self._init_alpha()

            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
                H = min(self.C, self.alpha[i1] + self.alpha[i2])
            else:
                L = max(0, self.alpha[i2] - self.alpha[i1])
                H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])

            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(
                self.X[i2],
                self.X[i2]) - 2 * self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue

            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (
                E1 - E2) / eta  #此处有修改，根据书上应该是E1 - E2，书上130-131页
            alpha2_new = self._compare(alpha2_new_unc, L, H)

            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
                self.alpha[i2] - alpha2_new)

            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b

            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2

            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new

            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'

    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])

        return 1 if r > 0 else -1

    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)

    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1) * self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w