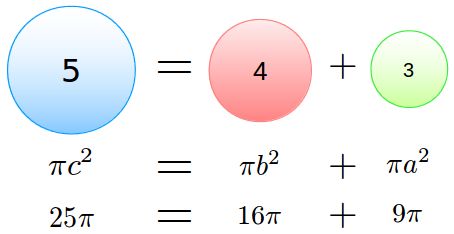修订|勾股定理的惊奇用途 -《更好的解释(数学篇)》02
2018.8.31 修改了文章2.4节一处公式错误, 感谢@Luka Modrić 朋友指正!
原文: https://betterexplained.com/articles/surprising-uses-of-the-pythagorean-theorem/译文: http://jakwings.is-programmer.com/posts/29536.html
勾股定理(毕达哥拉斯定理, a² + b² = c²)是非常有名的:如果一个公式可以像辛普森那样,那么它必然会出名。
但是我们通常认为这个公式只是应用在三角形与几何学中而已。但是再想想。只要涉及到平方数,那么毕达哥拉斯定理就可以应用在任何形状以及任何方程式中去。
请你继续读下去,看看这个已经有2500年历史的定理是如何帮助我们理解计算机科学,物理,甚至是Web 2.0所体现的社交价值。
2.1 理解面积是怎样计算的
我喜欢在一个古老的话题中有新的发现,并且可以挖掘出更深刻的东西。举例来说,直到我写完这个章节之前我发现其实自己一直没有深刻的理解面积这个概念。没错,我们可以快速的列举出大量的公式,但是我们真的理解面积的性质吗?
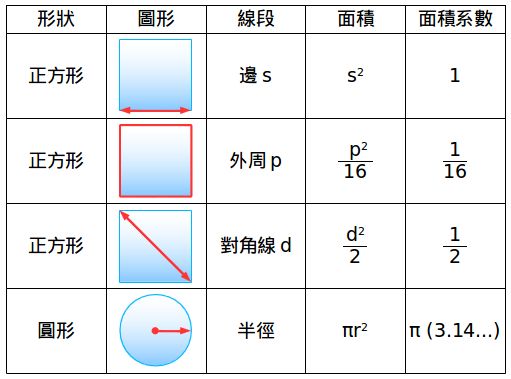
我们可以通过计算任意线段的平方来得到任意图形的面积
在正方形中,平方项就是正方形的一条边,而正方形的面积就是边的平方(边为5,那么面积就是25)。在圆中,这个线段指的是它的半径,而它的面积就是πr²(半径是5,那么面积就是25π)。相当容易。
我们可以任意选取线段,然后从中计算出面积:在每一种线段对应的面积公式中都有一个相应的面积系数:
面积=系数×(线段)²
举例来说,正方形中的对角线(“d”)。通常意义上的边等于 d/√2 ,所以面积就是 d²/2。在这个例子中如果我们选择使用对角线的平方计算面积,那么相应的面积常数就是 "1/2 ”。
现在,使用整个周长(“p”)作为线段,通常意义上的边长等于p/4,所以面积就是 p² /16。使用 p² 计算面积时所对应的面积系数就是1/16。
2.2 我们可以任意选取线段吗?
这是肯定的。因为在你选取的任意一条线段(比如说正方形的周长,正好是边长的四倍)总可以通过一定的关系与通常意义上计算面积的线段相联系起来(比如说正方形的边长)。因此我们可以通过“传统线段”与“新式线段”的转换来计算面积,我们怎样选择线段并不影响计算——只是相乘的面积系数会有所不同而已。
2.3 我们可以在任意形状中使用这一方法吗?
部分可以使用。一个给定的图形面积公式只适用于相似的图形,而这里类似指的是它们只是统一形状的不同缩放而已。这里举一些例子:
所有的正方形都是相似的(面积都是s²)
所有的圆也都是相似的(面积都是πr²)
不是所有的三角形都是相似的:有些是锐角三角形,有些是钝角三角形——根据选取线段的不同,每一种类型都有着各自的面积系数。改变了三角形的形状,它的面积公式也要改变。
是的,所有的三角形都可以通过面积=(1/2)·底·高来计算它的面积。但是底与高的关系依赖于三角形的形状,所以它们的面积系数也会有差异。
为什么我们需要相似性来保证它们可以使用相同的面积公式呢?直觉告诉我们,我们等比例缩放一个图形时,绝对大小会改变,但是比例却不会发生改变。一个正方形,无论它怎么缩放,都有周长=4·边长。
因为面积系数的选择基于图形的比例,所以任何拥有相同比例的图形都可以通过同一公式来计算面积。。这有些像所有人的臂展都近似等于身高。不管他是NBA球员还是一个孩子,他们都可以使用相同的公式因为他们都是相关的。(这种直觉化的论证可能并不会让数学家满意——但是在这个例子中,有什么问题可以去问问欧几里德)。
我希望这些更高级的概念能够说得通:
面积可以从任何线段的平方中得到,而不只是从边长或半径中
每一个线段都有相应的“面积系数”
相似的图形可以使用同一面积公式
但是有人会问:为什么相似的图形拥有一样的面积系数呢?以下是我的理解:
成比例的图形拥有相同的比例。为什么呢?当我们移动一个物体,显然它的大小会发生改变(比如说一个停止标志靠近或走远),但是它的比例不会发生变化。一个物体有可能知道它正在被远处的人观察,因而去改变自己的边长与面积的比例吗?
考虑两个相似的图形。把大的移动到远处,直到看起来它的大小与小的图形相等。现在它们看起来一样了,因此它们拥有相同的比例关系(比如说周长与面积)。现在拉动大的图形。它看起来更大了,但是在移动的过程中,它的比例关系并没有发生变化——它们就跟小图形的比例关系一样。
这是一位读者(Per Vognsen)更加正规的证明:
你只需要证明对于一类相似图形,L² /A是一个常数即可。在一类相似图形中任意选取两个图形,它们的面积分别是A与A' ,长度分别是L与L' 。令F是把一个图形映射到其他图形上的缩放系数。然后我们就得到A = F² * A',L = F * L' 。把长度平方即可得到 L²= F² * L'² 。面积方程除以该等式,F²便可以被消掉,同时得到A/L² = A/L'²。所以便可知面积与长度平方的比例确实为一常数。
2.4 直觉化的看待毕达哥拉斯定理
我想我们都承认毕达哥拉斯定理是成立的。但是许多证明都是一种机械化的理解:重新调整图形,瞧,这就证明了这个定理。但是这样很清楚吗,直观地看,那就是一定是 a²+ b²=c² 而不是 2a² + b²= c² 吗?不是的,让我们来直观地看看。
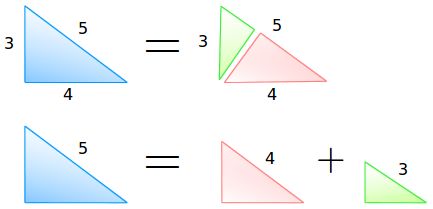
我们要用到一个至关重要的概念:任意直角三角形都可以分解成两个相似的直角三角形。
很酷,是吧?通过一个点画一条垂线就可以把一个直角三角形分成两个小直角三角形。几何爱好者们,试着自己证明一下这个命题:利用相似性中的角-角-角来证明。
这个示意图把一些事解释的很清楚:
面积(大)=面积(中)+面积(小)
这能说得通,对吧?小三角形是从大三角形中切出来的,所以面积就是把较小三角形的面积相加起来。而更让人意外的是:因为这些三角形都相似,所以它们的面积公式也都相同。
让我们把最长的边称为c(5),较小的边称为b(4),而最小的边长则称为c(3)。这种三角形的的面积公式就是:
面积=F×斜边²
这里的F是面积系数(在这里是6/25或0.24;具体是那个数值并不重要)。现在让我们利用以下方程式做运算:
面积(大)=面积(中)+面积(小)
F· c²= F· b² + F· a²
两边同除以F,便可以得到:
c²= b² + a²
这就是那个最著名的定理!你知道它是真的,但是你现在知道它为什么是真的:
一个三角形可以分成两个更小的相似三角形
因为面积是通过相加得到的,所以边长的平方()它决定了面积)也要相加。
这可能需要花点时间来想清楚,但是我希望结果对你来说是显而易见的。为什么小三角形相加没有得到一个更大的三角形呢?
实际上,毕达哥拉斯定理成立是基于欧几里德几何的假设,比如它在球体上便不再成立,但是我们会在以后再讨论这个问题。
2.5 一些应用:试试任意一种图形
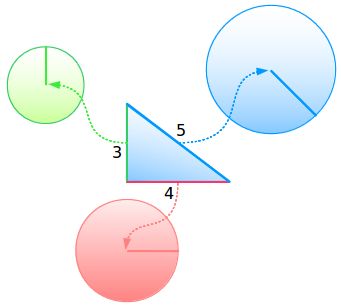
我们在示意图中利用了三角形,最简单的一种二维图形。但是线段可以是任意一种图形的线段。一圆形为例:
当我们把它们相加时会发生什么呢?
你猜到了吧:半径为5的圆=半径为4的圆+半径为3的圆。
相当神奇,是吧?我们可以把毕达哥拉斯定理乘以面积系数(比如说这个例子中的π),然后就得出了任意一种图形的关系。
记住,线段可以是图形的任意部分。我们可以选用圆的半径,直径,或者是圆周——尽管有着不同的面积系数,但是3-4-5 的关系始终成立。
所以,无论是披萨还是尼克松的面具你都可以相加,毕达哥拉斯定理帮助你把相似图形的面积联系起来。接下里就是一些你未曾在学校中学到的东西。
2.6 一些有用的应用:平方项守恒
毕达哥拉斯定理可以应用在任何有平方项的方程式中。
分割直角三角形意味着你可以把任意一个数(c²)分解为两个较小数字的和(a² + b²)。在现实生活中,边长的“长度”可以是距离,能量,工作,时间,甚至是在社交网络中的人们。
社交网络
麦卡福定理(Metcalfe's Law)(如果你相信的话)说网络的价值与 n²(关系的数量)有关。如下所示
50M的网络= 40M的网络+ 30M的网络
相当惊人——第二项网络与第三项网络共有 70M 的人,但是它们并不是简单的相加。一个有五千万人的网络跟它们加起来的价值相当。
计算机科学
一些程序如果有n个输入,那么就要花费 n² 的时间(比如说冒泡排序法)。耗费时间表示如下:
50个输入= 40个输入+ 30个输入
相当有意思。总共70个元素的两组输入跟一组50个元素输入所花费的时间相同。(是的,可能会有一些总开销或是启动开销有所不同,但在这里暂且不予以考虑)
根据这个关系,把元素进行分成子组进行运算就有意义了。事实上,一种较优的排序法——快速排序法中就用到了这一关系。毕达哥拉斯定理帮助我们理解了对50个元素进行排序跟对30个以及40个两组不同的元素进行排序,所消耗的时间是一样。
表面积
球面的表面积是 4πr²。所以就有:
半径为50的球面积= 半径为40的球面积+ 半径为30的球面积
我们并不经常用到球面积,但是船身有着一样的关系(船身就像是畸形化的球面,对吧?)。假设船只的形状都相似,给50英尺的游艇喷漆所用的颜料正好可以给40英尺与30英尺的游艇喷漆。呕耶!
物理
如果你还记得在物理课上学过的,一个质量为m,速度为v的物体的动能等于mv² /2。因此有
500迈的能量=400迈的能量+ 300迈的能量
加速一个子弹到500迈的能量,可以把两个同样的子弹分别加速到400迈与300迈。
2.7 享受你的新观点
经历了整个学校生涯我们一直认为毕达哥拉斯定理只与三角形和几何有关。但其实不是。
当你看到一个直角三角形时,你意识到它的边长可以代表任何图形的任意一个部分,或者是代表任何有平方项的方程中的一个变量。我发现这非常惊人。
这个定理还有许多有意思的地方,比如说测量任意长度。好好发掘吧。(完)