教程 | 概率编程：使用贝叶斯神经网络预测金融市场价格

2018 年 2 月 10 日 机器之心

选自Medium

作者：Alex Honchar

机器之心编译

参与：陈韵竹、李泽南

随着人工智能技术的普及，用机器学习预测市场价格波动的方法最近层出不穷。本文中，Alex Honchar 介绍了利用概率编程和 Pyro 进行价格预测的方法，相较于常规神经网络，新方法对于数据的依赖程度更小，结果更准确。在实验中，作者选择了最近流行的虚拟货币「以太币」作为实例进行价格预测。

去年我曾发表过几篇有关使用神经网络进行金融价格预测的教程，我认为其中有一部分结果至少还挺有意思，并且值得在实际交易中加以应用。如果你阅读过这些文章，你一定注意到一个现象：当你试图将一些机器学习模型应用于「随机」数据并希望从中找到隐藏规律的时候，训练过程往往会产生严重的过拟合。我们曾使用不同的正则化技术和附加数据应对这个问题，但是这不仅很费时，还有种盲目搜索的感觉。

今天，我想介绍一个略微有些不同的方法对同样的算法进行拟合。使用概率的观点看待这个问题能够让我们从数据本身学习正则化、估计预测结果的确定性、使用更少的数据进行训练，还能在模型中引入额外的概率依赖关系。我不会过多深入贝叶斯模型或变分原理的数学、技术细节，而是会给出一些概述，也更多地将讨论集中在应用场景当中。文中所用的代码可以在以下链接中找到：https://github.com/Rachnog/Deep-Trading/tree/master/bayesian

与此同时，我也推荐大家查阅我此前发布的基于神经网络的财务预测教程：

1. 简单时间序列预测（错误纠正完毕）

2. 正确一维时间序列预测+回测

3. 多元时间序列预测

4. 波动预测和自定义损失

5. 多任务和多模式学习

6. 超参数优化

7. 用神经网络进行经典策略强化

为了更深入地了解概率规划、贝叶斯模型以及它们的应用，我推荐你在以下资源网站中查看：

模式识别和机器学习
黑客贝叶斯方法
下面即将提到的库文件

另外，你还可能会用到下列 Python 库：

PyMC3 (https://github.com/pymc-devs/pymc3)
Edward (http://edwardlib.org/)
Pyro (http://pyro.ai/)

概率编程

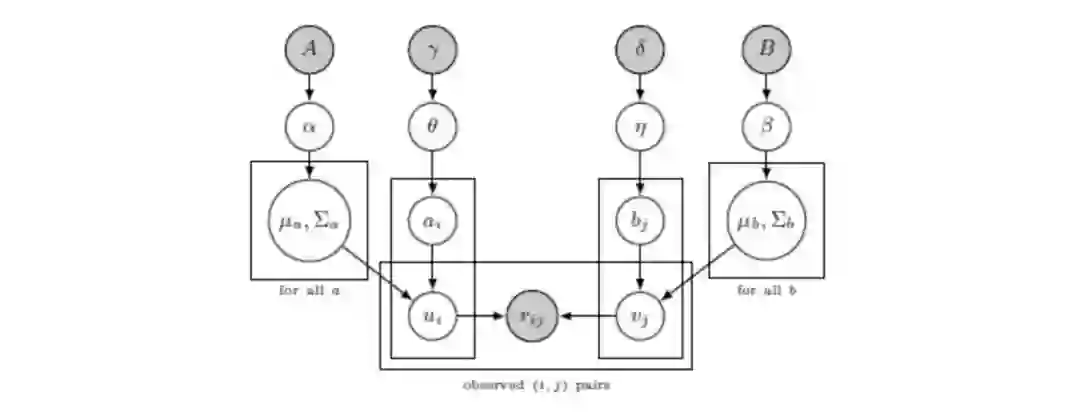
这个「概率」指的是什么？我们为什么称其为「编程」呢？首先，让我们回忆一下我们所谓「正常的」神经网络指的是什么、以及我们能从中得到什么。神经网络有着以矩阵形式表达的参数（权重），而其输出通常是一些标量或者向量（例如在分类问题的情况下）。当我们用诸如 SGD 的方法训练这个模型后，这些矩阵会获得固定值。与此同时，对于同一个输入样本，输出向量应该相同，就是这样！但是，如果我们将所有的参数和输出视为相互依赖的分布，会发生什么？神经网络的权重将与输出一样，是一个来自网络并取决于参数的样本——如果是这样，它能为我们带来什么？

让我们从基础讲起。如果我们认为网络是一个取决于其他分布的数集，这首先就构成了联合概率分布 p(y, z|x)，其中有着输出 y 和一些模型 z 的「内部」隐变量，它们都取决于输入 x（这与常规的神经网络完全相同）。我们感兴趣的是找到这样神经网络的分布，这样一来就可以对 y ~ p(y|x) 进行采样，并获得一个形式为分布的输出，该分布中抽取的样本的期望通常是输出，和标准差（对不确定性的估计）——尾部越大，则输出置信度越小。

这种设定可能不是很明确，但我们只需要记住：现在开始，模型中所有的参数、输入及输出都是分布，并且在训练时对这些分布进行拟合，以便在实际应用中获得更高的准确率。我们也需要注意自己设定的参数分布的形状（例如，所有的初识权重 w 服从正态分布 Normal（0,1），之后我们将学习正确的均值和方差）。初始分布即所谓的先验知识，在训练集上训练过的分布即为后验知识。我们使用后者进行抽样并得出结果。

图源：http://www.indiana.edu/~kruschke/BMLR/

模型要拟合到什么程度才有用？通用结构被称为变分推理（variational inference）。无需细想，我们可以假设，我们希望找到一个可以得到最大对数似然函数 p_w（z | x）的模型，其中 w 是模型的参数（分布参数），z 是我们的隐变量（隐藏层的神经元输出，从参数 w 的分布采样得到），x 是输入数据样本。这就是我们的模型了。我们在 Pyro 中引入了一个实例来介绍这个模型，该简单实例包含所有隐变量 q_（z）的一些分布，其中 ф 被称为变分参数。这种分布必须近似于训练最好的模型参数的「实际」分布。

训练目标是使得 [log(p_w(z|x))—log(q_ф(z))] 的期望值相对于有指导的输入数据和样本最小化。在这里我们不探讨训练的细节，因为这里面的知识量太大了，此处就先当它是一个可以优化的黑箱吧。

对了，为什么需要编程呢？因为我们通常将这种概率模型（如神经网络）定义为变量相互关联的有向图，这样我们就可以直接显示变量间的依赖关系：

图源：http://kentonmurray.com/

而且，概率编程语言起初就被用于定义此类模型并在模型上做推理。

为什么选择概率编程？

不同于在模型中使用 dropout 或 L1 正则化，你可以把它当作你数据中的隐变量。考虑到所有的权重其实是分布，你可以从中抽样 N 次得到输出的分布，通过计算该分布的标准差，你就知道能模型有多靠谱。作为成果，我们可以只用少量的数据来训练这些模型，而且我们可以灵活地在变量之间添加不同的依赖关系。

概率编程的不足

我还没有太多关于贝叶斯建模的经验，但是我从 Pyro 和 PyMC3 中了解到，这类模型的训练过程十分漫长且很难定义正确的先验分布。而且，处理从分布中抽取的样本会导致误解和歧义。

数据准备

我已经从 http://bitinfocharts.com/ 抓取了每日 Ethereum（以太坊）的价格数据。其中包括典型的 OHLCV（高开低走），另外还有关于 Ethereum 的每日推特量。我们将使用七日的价格、开盘及推特量数据来预测次日的价格变动情况。

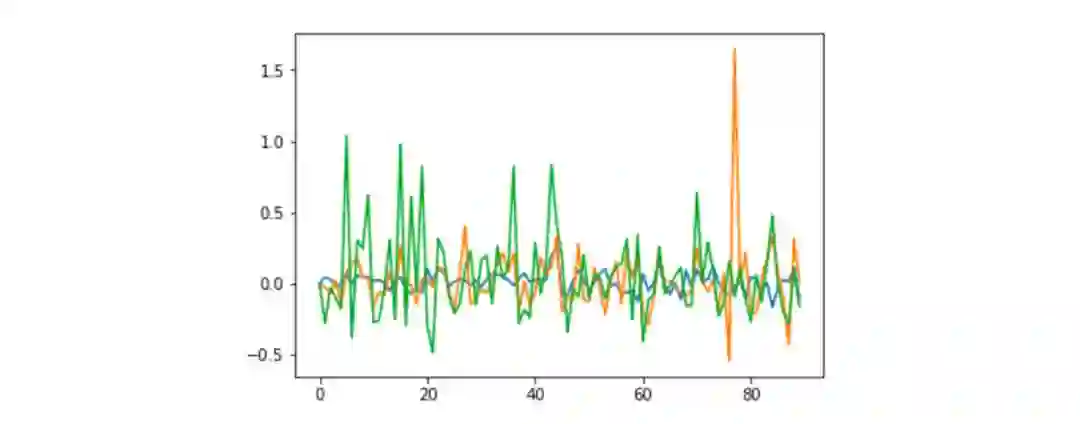
价格、推特数、大盘变化

上图是一些数据样本——蓝线对应价格变化，黄线对应推特数变化，绿色对应大盘变化。它们之间存在某种正相关（0.1—0.2）。因此我们希望能利用好这些数据中的模式对模型进行训练。

贝叶斯线性回归

首先，我想验证简单线性分类器在任务中的表现结果（并且我想直接使用 Pyro tutorial——http://pyro.ai/examples/bayesian_regression.html——的结果）。我们按照以下操作在 PyTorch 上定义我们的模型（详情参阅官方指南：http://pyro.ai/examples/bayesian_regression.html）。

  
    
    
    
   
     
     
     class RegressionModel(nn.Module):
   
     
     
         def __init__(self, p):
   
     
     
             super(RegressionModel, self).__init__()
   
     
     
             self.linear = nn.Linear(p, 1)
   
     
     
     def forward(self, x):
   
     
     
             # x * w + b
   
     
     
             return self.linear(x)

以上是我们以前用过的简单确定性模型，下面是用 Pyro 定义的概率模型：

  
    
    
    
   
     
     
     def model(data):
   
     
     
         # Create unit normal priors over the parameters
   
     
     
         mu = Variable(torch.zeros(1, p)).type_as(data)
   
     
     
         sigma = Variable(torch.ones(1, p)).type_as(data)
   
     
     
         bias_mu = Variable(torch.zeros(1)).type_as(data)
   
     
     
         bias_sigma = Variable(torch.ones(1)).type_as(data)
   
     
     
         w_prior, b_prior = Normal(mu, sigma), Normal(bias_mu, bias_sigma)
   
     
     
         priors = {'linear.weight': w_prior, 'linear.bias': b_prior}
   
     
     
         lifted_module = pyro.random_module("module", regression_model, priors)
   
     
     
         lifted_reg_model = lifted_module()
   
     
     
     with pyro.iarange("map", N, subsample=data):
   
     
     
             x_data = data[:, :-1]
   
     
     
             y_data = data[:, -1]
   
     
     
             # run the regressor forward conditioned on inputs
   
     
     
             prediction_mean = lifted_reg_model(x_data).squeeze()
   
     
     
             pyro.sample("obs",
   
     
     
                         Normal(prediction_mean, Variable(torch.ones(data.size(0))).type_as(data)),
   
     
     
                         obs=y_data.squeeze())

从上面的代码可知，参数 W 和 b 均定义为一般线性回归模型分布，两者都服从正态分布 Normal（0,1）。我们称之为先验，创建 Pyro 的随机函数（在我们的例子中是 PyTorch 中的 RegressionModel），为它添加先验 ({『linear.weight』: w_prior, 『linear.bias』: b_prior})，并根据输入数据 x 从这个模型 p(y|x) 中抽样。

这个模型的 guide 部分可能像下面这样：

  
    
    
    
   
     
     
      def guide(data):
   
     
     
         w_mu = Variable(torch.randn(1, p).type_as(data.data), requires_grad=True)
   
     
     
         w_log_sig = Variable(0.1 * torch.ones(1, p).type_as(data.data), requires_grad=True)
   
     
     
         b_mu = Variable(torch.randn(1).type_as(data.data), requires_grad=True)
   
     
     
         b_log_sig = Variable(0.1 * torch.ones(1).type_as(data.data), requires_grad=True)
   
     
     
         mw_param = pyro.param("guide_mean_weight", w_mu)
   
     
     
         sw_param = softplus(pyro.param("guide_log_sigma_weight", w_log_sig))
   
     
     
         mb_param = pyro.param("guide_mean_bias", b_mu)
   
     
     
         sb_param = softplus(pyro.param("guide_log_sigma_bias", b_log_sig))
   
     
     
         w_dist = Normal(mw_param, sw_param)
   
     
     
         b_dist = Normal(mb_param, sb_param)
   
     
     
         dists = {'linear.weight': w_dist, 'linear.bias': b_dist}
   
     
     
         lifted_module = pyro.random_module("module", regression_model, dists)
   
     
     
         return lifted_module()

我们定义了想要「训练」的分布的可变分布。如你所见，我们为 W 和 b 定义了相同的分布，目的是让它们更接近实际情况（据我们假设）。这个例子中，我让分布图更窄一些（服从正态分布 Normal(0, 0.1)）

然后，我们用这种方式对模型进行训练：

  
    
    
    
   
     
     
         for j in range(3000):
   
     
     
         epoch_loss = 0.0
   
     
     
         perm = torch.randperm(N)
   
     
     
         # shuffle data
   
     
     
         data = data[perm]
   
     
     
         # get indices of each batch
   
     
     
         all_batches = get_batch_indices(N, 64)
   
     
     
         for ix, batch_start in enumerate(all_batches[:-1]):
   
     
     
             batch_end = all_batches[ix + 1]
   
     
     
             batch_data = data[batch_start: batch_end]
   
     
     
             epoch_loss += svi.step(batch_data)

在模型拟合后，我们想从中抽样出 y。我们循环 100 次并计算每一步的预测值的均值和标准差（标准差越高，预测置信度就越低）。

  
    
    
    
   
     
     
        preds = []
   
     
     
     for i in range(100):
   
     
     
         sampled_reg_model = guide(X_test)
   
     
     
         pred = sampled_reg_model(X_test).data.numpy().flatten()
   
     
     
         preds.append(pred)

现在有很多经典的经济预测度量方法，例如 MSE、MAE 或 MAPE，它们都可能会让人困惑——错误率低并不意味着你的模型表现得好，验证它在测试集上的表现也十分重要，而这就是我们做的工作。

使用贝叶斯模型进行为期 30 天的预测

从图中我们可以看到，预测效果并不够好。但是预测图中最后的几个跳变的形状很不错，这给了我们一线希望。继续加油！

常规神经网络

在这个非常简单的模型进行实验后，我们想要尝试一些更有趣的神经网络。首先让我们利用 25 个带有线性激活的神经元的单隐层网络训练一个简单 MLP：

  
    
    
    
   
     
     
      def get_model(input_size):
   
     
     
         main_input = Input(shape=(input_size, ), name='main_input')
   
     
     
         x = Dense(25, activation='linear')(main_input)
   
     
     
         output = Dense(1, activation = "linear", name = "out")(x)
   
     
     
         final_model = Model(inputs=[main_input], outputs=[output])
   
     
     
         final_model.compile(optimizer='adam',  loss='mse')
   
     
     
         return final_model

训练 100 个 epoch：

  
    
    
    
   
     
     
     model = get_model(len(X_train[0]))
   
     
     
     history = model.fit(X_train, Y_train, 
   
     
     
                   epochs = 100, 
   
     
     
                   batch_size = 64, 
   
     
     
                   verbose=1, 
   
     
     
                   validation_data=(X_test, Y_test),
   
     
     
                   callbacks=[reduce_lr, checkpointer],
   
     
     
                   shuffle=True)

其结果如下：

使用 Keras 神经网络进行为期 30 天的预测

我觉得这比简单的贝叶斯回归效果更差，此外这个模型不能得到确定性的估计，更重要的是，这个模型甚至没有正则化。

贝叶斯神经网络

现在我们用 PyTorch 来定义上文在 Keras 上训练的模型：

  
    
    
    
   
     
     
     class Net(torch.nn.Module):
   
     
     
         def __init__(self, n_feature, n_hidden):
   
     
     
             super(Net, self).__init__()
   
     
     
             self.hidden = torch.nn.Linear(n_feature, n_hidden)   # hidden layer
   
     
     
             self.predict = torch.nn.Linear(n_hidden, 1)   # output layer
   
     
     
     def forward(self, x):
   
     
     
             x = self.hidden(x)
   
     
     
             x = self.predict(x)
   
     
     
             return x

相比于贝叶斯回归模型，我们现在有两个参数集（从输入层到隐藏层的参数和隐藏层到输出层的参数），所以我们需要对分布和先验知识稍加改动，以适应我们的模型：

  
    
    
    
   
     
     
     priors = {'hidden.weight': w_prior, 
   
     
     
                   'hidden.bias': b_prior,
   
     
     
                   'predict.weight': w_prior2,
   
     
     
                   'predict.bias': b_prior2}

以及 guide 部分：

  
    
    
    
   
     
     
     dists = {'hidden.weight': w_dist, 
   
     
     
                   'hidden.bias': b_dist,
   
     
     
                   'predict.weight': w_dist2,
   
     
     
                   'predict.bias': b_dist2}

请不要忘记为模型中的每一个分布起一个不同的名字，因为模型中不应存在任何歧义和重复。更多代码细节请参见源代码：https://github.com/Rachnog/Deep-Trading/tree/master/bayesian

训练之后，让我们看看最后的结果：

使用 Pyro 神经网络进行为期 30 天的预测

它看起来比之前的结果都好得多！

比起常规贝叶斯模型，考虑到贝叶斯模型所中习得的权重特征或正则化，我还希望看到权重的数据。我按照以下方法查看 Pyro 模型的参数：

  
    
    
    
   
     
     
     for name in pyro.get_param_store().get_all_param_names():
   
     
     
         print name, pyro.param(name).data.numpy()

这是我在 Keras 模型中所写的代码：

  
    
    
    
   
     
     
     import tensorflow as tf
   
     
     
     sess = tf.Session()
   
     
     
     with sess.as_default():
   
     
     
         tf.global_variables_initializer().run()
   
     
     
     dense_weights, out_weights = None, None
   
     
     
     with sess.as_default():
   
     
     
         for layer in model.layers:
   
     
     
             if len(layer.weights) > 0:
   
     
     
                 weights = layer.get_weights()
   
     
     
                 if 'dense' in layer.name:
   
     
     
                     dense_weights = layer.weights[0].eval()
   
     
     
                 if 'out' in layer.name:
   
     
     
                     out_weights = layer.weights[0].eval()

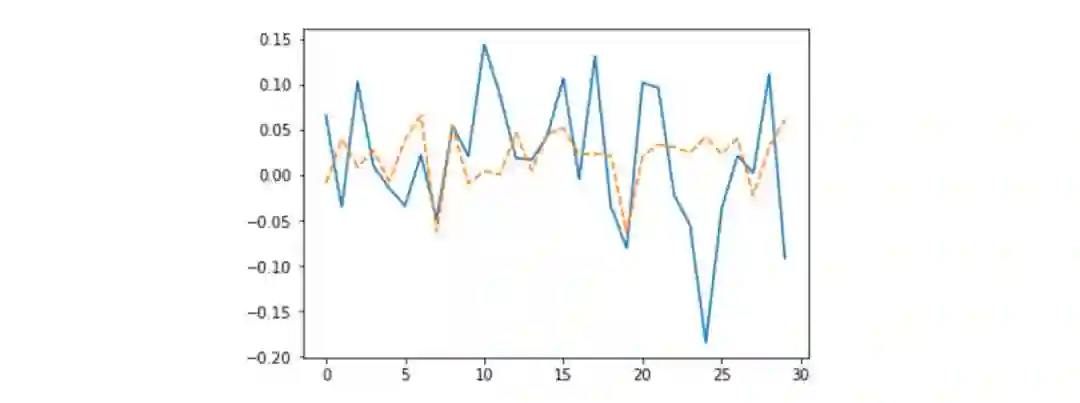
例如，Keras 模型最后一层的权重的均值和标准差分别为 -0.0025901748 和 0.30395043，Pyro 模型对应值为 0.0005974418 和 0.0005974418。数字小了很多，但效果真的不错！其实这就是 L2 或 Dropout 这种正则化算法要做的——把参数逼近到零，而我们可以用变分推理来实现它！隐藏层的权重变化更有趣。我们将一些权重向量绘制成图，蓝线是 Keras 模型的权重，橙线是 Pyro 模型的权重：

输入层与隐藏层之间的部分权重

真正有意思的不止是权重的均值与标准差变得小，还有一点是权重变得稀疏，所以基本上在训练中完成了第一个权重集的稀疏表示，以及第二个权重集的 L2 正则化，多么神奇！别忘了自己跑跑代码感受一下：https://github.com/Rachnog/Deep-Trading/tree/master/bayesian

小结

我们在文中使用了新颖的方法对神经网络进行训练。不同于顺序更新静态权重，我们是更新的是权重的分布。因此，我们可能获得有趣又有用的结果。我想强调的是，贝叶斯方法让我们在调整神经网络时不需要手动添加正则化，了解模型的不确定性，并尽可能使用更少的数据来获得更好的结果。感谢阅读：)