The Tsetlin Machine – 一种博弈论驱动的使用命题逻辑的最优模式识别方法

The Tsetlin Machine – A Game Theoretic Bandit Driven Approach to Optimal Pattern Recognition with

Propositional Logic∗Ole-Christoffer Granmo†

Abstract

Although simple individually, artificial neurons provide state-of-the-art performance when interconnected in deep networks. Unknown to many, there exists an arguably even simpler and more versatile learning mechanism, namely, the Tsetlin Automaton. Merely by means of a single integer as memory, it learns the optimal action in stochastic environ- ments through increment and decrement operations. In this paper, we introduce the Tsetlin Machine, which solves complex pattern recognition problems with easy-to-interpret propo- sitional formulas, composed by a collective of Tsetlin Automata. To eliminate the long- standing problem of vanishing signal-to-noise ratio, the Tsetlin Machine orchestrates the automata using a novel game. Our theoretical analysis establishes that the Nash equilibria of the game align with the propositional formulas that provide optimal pattern recognition accuracy. This translates to learning without local optima, only global ones. We argue that the Tsetlin Machine finds the propositional formula that provides optimal accuracy, with probability arbitrarily close to unity. In five benchmarks, the Tsetlin Machine provides competitive accuracy compared with SVMs, Decision Trees, Random Forests, Naive Bayes Classifier, Logistic Regression, and Neural Networks. The Tsetlin Machine further has an inherent computational advantage since both inputs, patterns, and outputs are expressed as bits, while recognition and learning rely on bit manipulation. The combination of accuracy, interpretability, and computational simplicity makes the Tsetlin Machine a promising tool for a wide range of domains. Being the first of its kind, we believe the Tsetlin Machine will kick-start new paths of research, with a potentially significant impact on the AI field and the applications of AI.

Keywords: Bandit Problem, Game Theory, Interpretable Pattern Recognition, Propo- sitional Logic, Tsetlin Automata Games, Online Learning

1.5 Paper Contributions

In this paper, we attack the limited pattern expression capability and vanishing signal-to-noise ratio of learning automata based pattern recognition, introducing the Tsetlin Machine. The contributions of the paper can be summarized as follows:

• We introduce the Tsetlin Machine, which solves complex pattern recognition problems with propositional formulas, composed by a collective of Tsetlin Automata.

• 
  

• We eliminate the longstanding vanishing signal-to-noise ratio problem with a unique decentralized learning scheme based on game theory [30, 2]. The game we have designed allows thousands of Tsetlin Automata to successfully cooperate.

• 
  

• The game orchestrated by the Tsetlin Machine is based on resource allocation principles [31], in inter-play with frequent itemset mining [16]. By allocating sparse pattern rep- resentation resources according to the frequency of the patterns, the Tsetlin Machine is able to capture intricate unlabelled sub-patterns, for instance addressing the so-called Noisy XOR-problem.

• 
  

• Our theoretical analysis establishes that the Nash equilibria of the game are aligned with the propositional formulas that provide optimal pattern recognition accuracy. This translates to learning without local optima, only global ones.

• 
  

• We further argue that the Tsetlin Machine finds a propositional formula that provides optimal pattern recognition accuracy, with probability arbitrarily close to unity.

• 
  

• The propositional formulas are represented as bit patterns. These bit patterns are rela- tively easy to interpret, compared to e.g. a neural network (see Table 1 for an example bit pattern). This facilitates human quality assurance and scrutiny, which for instance can be important in safety-critical domains such as medicine.

• 
  

• The Tsetlin Machine is a new approach to global construction of decision rules. We demonstrate that decision rules for large-scale pattern recognition can be learned on- line, under particularly noisy conditions. To establish a common reference point towards related work in interpretable pattern recognition, we include empirical results on decision trees.

• 
  

• The Tsetlin Machine is particularly suited for digital computers, being directly based on bit manipulation with AND-, OR-, and NOT operators. Both input, hidden pat- terns, and output are represented directly as bits, while recognition and learning rely on manipulating those bits.

  
  

• In our empirical evaluation on five datasets, the Tsetlin Machine provides competitive per- formance in comparison with Multilayer Perceptron Networks, Support Vector Machines, Decision Trees, Random Forests, the Naive Bayes Classifier, and Logistic Regression.

  
  

• 
  

• It further turns out that the Tsetlin Machine requires less data than neural networks, outperforming even the Naive Bayes Classifier in data sparse environments.

• 
  

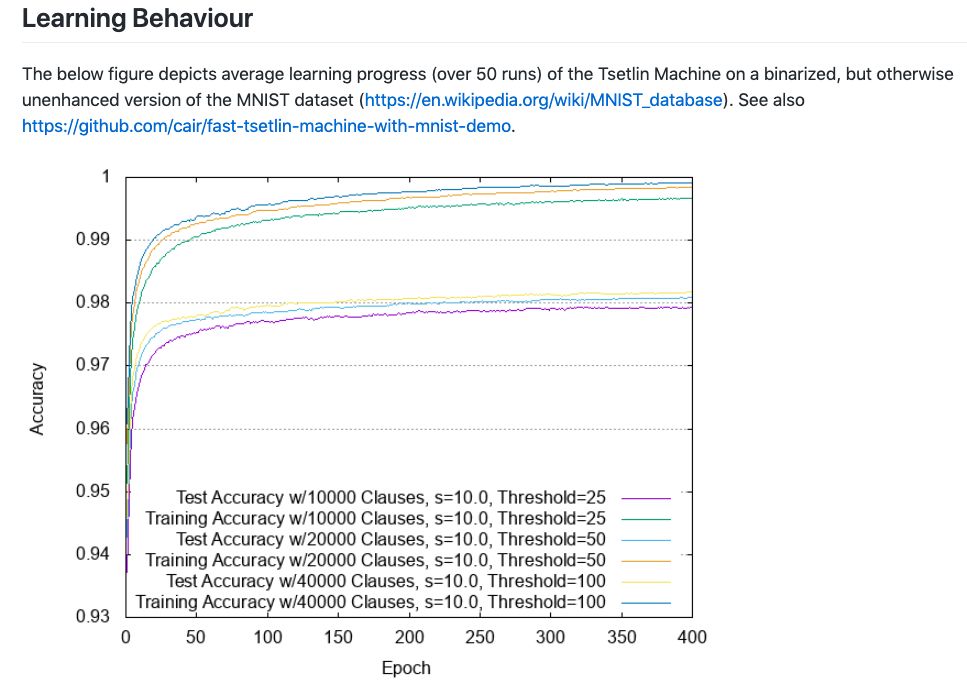
• Overfitting is inherently combated by leveraging frequent itemset mining [16]. Even while accuracy on the training data approaches 99.9%, mean accuracy on the test data continues to increase as well. This is quite different from the behaviour of back-propagation in neural networks, where accuracy on test data starts to drop at some point, without proper regularization mechanisms.

• 
  

  We demonstrate how the Tsetlin Machine can be used as a building block to create more advanced architectures.

• We believe that the combination of accuracy, interpretability, and computational simplicity makes the Tsetlin Machine a promising tool for a wide range of domains. Being the first of its kind, we further believe it will kick-start completely new paths of research, with a potentially significant impact on the field of AI and the applications of AI.

论文代码：https://github.com/cair/pyTsetlinMachine

欢迎加入打卡群自律学习强化学习，更欢迎支持或加入我们一起来刷榜！更多内容请访问公众号CreateAMind菜单。

来刷你爱的榜！