知道吗？滚还是不滚的问题和信息论有关！

会员服务 ·

知道吗？滚还是不滚的问题和信息论有关！

2017 年 10 月 23 日 中科院物理所 宜城漫士

信息社会，信息的概念我们听得太多了，有时候会有梗说“这个信息量有点大啊……”比如下面的这个老掉牙的故事：

一对情侣被杀人狂抓住了

杀人狂说可以只杀一个，情侣两人玩一次剪刀石头布，胜方活命，平局两人都要死。

情侣互相约定好，一起出石头共赴黄泉！

可是最后女孩被杀人狂杀了，因为男孩出了剪刀。

但是，你有没有想过，一个精确的对于信息的定义是什么呢？是可以脑补出很多内容的意思吗？我们不妨深入思考一下信息，information，核心本质的意义在哪里。

在追求精确的科学领域，信息要有一个精确的量化指标。大概是说，我们可以有诸如“一个单位的信息”这样的说法。为了探求这样的量化方式，我们需要探索一下一些常见的信息载体给我们多或者少的信息的时候，有什么特点。

震惊！

太阳今天早晨竟然在东边升起！

不看你会后悔！

朝鲜声称即将进行下一轮核试验！

注意了！

每吸烟一分钟生命就会减少60秒！

看到这样的新闻标题，我们会觉得十分无聊，甚至不用看正文就知道这个新闻没有什么新东西（换句话说就是没有多少信息）。

那么这是为什么呢？

仔细思考一下你就会发现，之所以觉得这件事没什么值得报道的，核心原因就是因为我们觉得这件事情几乎是必然发生的，也就是说概率几乎为1。所以对于这些报道而言，它们包含的信息微乎其微。

但是相反，如果你突然看到了下面的消息：

国足3:0横扫巴西，

强势进军世界杯决赛！

神剧！

这个反派一句没BB就崩了男主！

LR脱单了！……

”

当你们看到这些概率非常小的事情的时候，立刻会觉得这背后充满了信息。因为可能性太小，所以背后一定有大事情。

于是我们就有了信息的第一个性质：

一个事件包含的信息和它发生的概率有关，且成负相关关系

（即概率越大信息越少，概率趋近于0信息无穷大）

但是这样的函数有很多(例如1/x^n-1)，我们还需要更加精确的定量分析信息的性质。稍加思考我们会感受到，假设存在这样表示信息量一个函数I(A)，以发生概率p的事件A为自变量；如果说有两件基本毫不相关的事情同时发生（例如特朗普当选总统和今天的线性代数停课），它们提供给我的总信息量，应当等于两个各自信息量的总和：

I(AB)=I(A)+I(B)

AB:特朗普当选总统且线性代数停课

A：特朗普当选总统

B：线性代数停课

但同时我们知道，不相关的AB发生的概率是两个事件的概率的乘积，所以这个性质精确的刻画了信息函数的样子，解这个函数方程，我们得到：

I(A)=log(1/p)

其中p是A发生的概率。

这个函数非常优秀，因为它同时满足了：

p=1时信息为0，p趋向于0时信息为无穷大

I(A)+I(B)=log(1/p)+log(1/q)

=log(1/pq)=I(AB)

（即信息的叠加原理）

在上面的这个公式中，log的底数是不清的。如果取成2，那么就是最常见的信息度量，单位为bit（没错！就是文件大小的那个bit！事实上它的含义就是基本内存单元的一个二进制码）；如果是自然对数e，那么单位就叫奈特。

可是，仅仅有了这个公式有什么意义呢？为了说明这个问题，我们可以先看一个有趣的小问题：

国王召开宴会，一共有1000桶葡萄酒。邪恶的刺客在其中一桶酒里下了致命的毒。人们只知道有且仅有一桶酒被下毒，却不知道是哪一桶。现在你可以拿小白鼠做实验，小白鼠可以同时喝下多个桶的取样结果，且无视稀释效果喝到就死，但是一只小白鼠只能喝一次，且时间紧迫你只有一轮观察的时间。请问你最少需要多少只小白鼠来确定呢？

这道题原本是一个数学竞赛的题目，最后的答案和二进制有关，但是这个问题原来的解法十分玄妙，如果没有接触过很难下手。不过，我们现在可以从信息论的角度来重新审视这个问题：

假设某一个小白鼠以p的概率死亡，(1-p)的概率存活。那么它最后的死活结果将会以p的概率通过死给出log(1/p)的信息，以(1-p)的概率通过活给出log(1/(1-p))的信息，所以每一只小白鼠给的信息量是：

p×log(1/p)+(1-p)×log(1/(1-p))

注意到函数x·log(x)是一个在(0,1)区间内的凸函数，所以根据琴生不等式我们有

p×log(1/p)+(1-p)×log(1/(1-p))≤2(1/2×log(2))=1

换句话说，每一个老鼠能够给出至多1bit的信息量，而1000桶酒我们假设每一桶都等概率1/1000的有毒（根据琴生不等式这也是最不确定和需要最多信息的情况了），于是这个信息量是：

log(1000)≈9.97<10

所以我们立刻得到，想要让小白鼠加在一起包含这个有毒的编号的信息，我们需要至少10只小白鼠。而且想要真正满足这一点，需要要求不同小白鼠之间的死活没有关联且每只老鼠的死亡概率都大致是1/2

而具体的做法很简单，我们把所有1-1000的数字写成十位二进制数，然后让第i只老鼠喝二进制第i位为1的所有编号桶的酒。这样，第i只老鼠如果死我们就知道有毒桶的第i位编号是1、否则是0，最后10只小白鼠的死活就自动构成有毒桶的编号的二进制序列，我们就确定下来有毒的是哪一桶酒了。

（以8桶酒为例，第一只小白鼠喝1,3,5,7;第二只喝3,4,7,8;第三只喝5,6,7,8。可以自己验证对于所有的有毒情况都唯一对应一个独特的死亡序列）

因此可以看到，一个信息源头的信息量有多少，很大程度上就是由它输出的多种情况及各种情况的概率分布所决定的。而量化其大小的标准，就是编码其各种输出的结果所需要的长度。一个良好的编码在相当长的一个时间跨度和随机分布内，应该使得其冗余编码最小，也就是总长度最短。在给定先验的信号分布（也就是各种结果可能的概率的时候），理论上最佳也被广泛使用的编码体系就是“哈夫曼编码”，有兴趣可以自己查找【挖坑不填嘿嘿嘿】

熵与互信息

为了让问题进行的更深入，我们先来看热力学的概念：熵，如何在信息中有应用。

熵在热力学中的意义是不确定度，在信息论中也有涉及（这就是香农建立起的信息熵理论）。如果一件事情有各种发生的可能，那么这个事情在位置的时候具有的不确定性（也就是熵），等于各种结果的信息量按照其概率加权平均。

我们可以看一个更有意思的事情，就是互信息：

如果仅仅有一个信息量的定义和量化我们并不能做什么事情。信息一件最重要的职能就是辅助我们减少不确定度、并完成一件事情。

比如当你选了一门Yariv的英语课，然后获得了几位学长在这门课上被挂或是被扔出教室的信息，那么你选择退课的几率将大大提升，换言之退掉Yariv课这件事情的不确定性（或信息量）在给定有学长被扔出教室的情况下会大大减小。

这种一个事件的发生的信息减少另一件事件的不确定度（也即信息量）的情况，就是互信息的意义所在。如果我们记：

X：得知惨惨的学长被挂及扔出教室

Y：选择退掉Yariv的英语课

然后我们有以下表格：

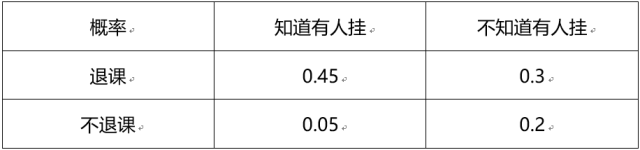
解释这个表格意思就是，

p(X)=0.5

你有0.5的概率知道有学长被挂的这件事情。

在你不知道的时候，你会有0.6的概率退课，0.4的概率不退；而你一旦知道这件事情之后，你有0.9的概率退课，0.1的概率选择面对疾风。在不知道你到底有没有听说学长的建议之前，你有0.45+0.3=0.75的概率退课，0.25的概率不退，这件事情的信息熵为

H(Y)=0.75×log(1/0.75)+0.25×log(1/0.25)

≈0.81bit

但是在给定X=1（也就是你知道有人被挂的事情的情况下），你退课的概率暴增到0.9,于是你退课这件事情的信息熵变成了只有

H(Y|X)=0.9×log(1/0.9)+0.1×log(1/0.1)

≈0.47bit

这中间减少的信息H(Y)-H(Y|X)≈0.34bit就是X给Y提供的信息了，我们把它记为I(Y:X)。通俗来说就是，X的发生能够给Y减少多少的不确定度。这个减少量就是信息量。

【小思考：I(X:Y)又代表什么呢？（答案在本文找）】

表示在知道你已经退课时候，能推出你听说了学长退课的信息量

信道模型

互信息有一个常见的模型是信道模型：众所周知，当信号在传递的时候会有一定的几率错误（电磁噪音，敲键盘手抖，女朋友很作……）我们假设当发送源打算发送0的时候有e的概率发生错误，打算发送1的时候有f的概率发生错误。而这个信道原本发出0的概率是p，那么整个传递过程如下表：

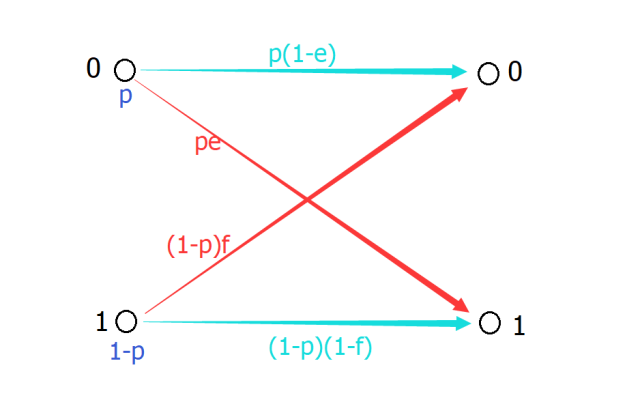
如图，蓝色代表正确传递，红色代表错误

我们可以看到，发出源s的信息熵为p×log(1/p)+(1-p)×log(1/(1-p)),而接受源r的信息熵为

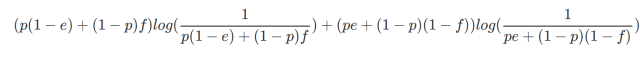
（不要觉得很复杂哦，只要注意到输出端以p(1-e)+(1-p)f的概率输出0，剩余概率输出1，然后两者的信息加权平均，这个公式还是很直观的）

上面的内容可能还是太抽象，我们不妨来看看一个真实的案例。

案例：某一个时候，你惹你女朋友生气了，这个时候她可能叫你滚，也可能不叫你滚。但是当她叫你滚的时候可能并不是真的让你滚，当她说再留一下的时候也可能是让你赶紧离开，这个时候她说出来的话对于你应该离开与否提供的信息如何呢？

其实很简单，套用上面的思路，设女朋友的表现是X，你应该要做的事情是Y。你需要计算的实质就是当你被给定X的时候你所能减少的Y的不确定度。也即I(Y:X)，这一点只要套用上面的公式把两边的信息熵减一下就可以了。

但是问题来了！You know what, 有一个非常极端的例子。那就是根据你的大数据统计测算，每次发生不愉快时，对方有正好0.5的概率让你滚，0.5的概率不。而当对方表达出任何一种想法的时候，都有0.5的概率是真的，0.5的概率言不由衷。这种情况下，如果你计算I(X:Y)就会惊奇的发现：

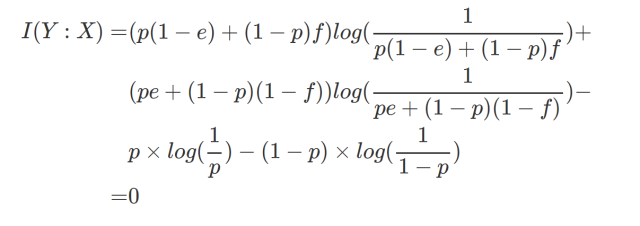
互信息为0啊！

为0啊老铁！

知道这意味着什么吗？

这意味着对方无论说什么，对于你究竟应该怎么做毫无指导意义，你完全不能得到任何信息。所以这个时候推荐你选择一个1bit熵的输出信源，然后自行决定，画风如下：

【以下情节纯属娱乐，如实际试验概不负责囧】

今天你似乎又惹你的女朋友生气了，但是她看起来十分平静，静静伫立着望向远方，不知道内心是不是充满波澜；在以往的经验里，她此时将以二分之一的概率碎碎念着。你去找她，问：“没事吧？”，答：“没事”，甚至还有一弯浅浅的笑。但是你依然放不下心，因为根据以往的经验，她此时有百分之五十的概率在说假话。你计算了互信息，发现根本没有任何头绪。此时你想到你需要一个1bit的信源来做出决定，于是你掏出了一枚硬币，你知道它等概率的正反在信息的本质上和她有没有生气一样，也在本质上和你基于她的表现做出离开与否的决定一样。于是你抛出这枚硬币，反面，看来她是真的不生气…………

【全文终】