深度牛顿！24岁博士小哥用图神经网络重新发现宇宙

---

  新智元报道  

编辑：白峰、舒婷

【新智元导读】深度学习模型取得了很大进展，但是依旧难以解释。传统的符号模型可以很好地解释和泛化，但高维数据又不好处理，那二者能否优势互补呢？近日，普林斯顿大学的博士Miles Cranmer发表了一篇论文，将符号模型和深度学习模型结合了起来，给天体物理学带来了新的惊喜！

19岁时，Miles Cranmer读了一篇物理学家李 · 斯莫林的采访。其中的一句话改变了他整个职业生涯的研究方向：

 

「让我们把注意力集中在量子理论和相对论及其关系上，如果我们成功了，将需要几代人的时间来理清由此衍生的知识。我们仍在忙于完成爱因斯坦掀起的革命，毫无疑问，这是一个漫长的过程。」

 

Cranmer读完之后深感不安，「 在我生命的尽头，我们对物理学的理解已经达到了极限， 我感到沮丧，因为无论我多么努力地工作，也许永远无法找到其中的终极奥秘。」

 

但是...  也许我们可以找到一种方法来打破这个限制。人工智能提出了一种新的科学探究机制，我们可以自动化研究过程本身。这个领域知识的增长是指数级的，而不是线性的，所以有了新的可能。

                Cranmer自己设计的个人主页，致力于用AI加速天体物理学进展

图神经网络更擅长知识发现，符号表达泛化能力更强

为了使科学自动化，我们需要把知识发现自动化。 然而，什么时候机器学习模型才能变成知识？为什么麦克斯韦方程组被认为是科学事实，而深度学习模型只是数据的插值？

 

首先，深度学习不能像符号模型一样概括物理模型。然而，似乎也存在一些使用简单符号模型描述物理世界的例子。

 

从纯机器学习的角度来看， 符号模型也拥有许多优点: 它们紧凑，提供了明确的解释，并且概括得很好。 「符号回归」就是这样一种用于符号模型的机器学习算法: 它是一种有监督的技术，用组合分析来为数据集建模。

 

然而，通常人们使用的是遗传算法(基本上是像施密特和利普森(2009年)那样的蛮力程序) ，这种算法的输入特征很难扩展。因此，许多机器学习问题尤其是高维数据的，仍然很棘手。

 

而深度学习最擅长高维数据建模，但是泛化性和可解释性差。那么，是否有一种方法可以将两者的优势结合起来呢？

 

深度模型不仅仅是预测目标，而且可以将目标分解为低维空间上运行的小型内部函数进行预测。 然后用符号回归解析表达式逼近深度模型的每个内部函数。最后提取出符号表达式，得到一个等价的解析模型。

 

我们选择「图神经网络」(GNN)作为基础架构，将内部结构分解为三个模块，并行表示粒子的相互作用。GNN 的「消息函数」类似于一个力，「节点更新函数」类似于牛顿运动定律。

                

通过鼓励 GNN 中的消息变得更稀疏，降低了每个函数的维数，使得符号回归更容易提取表达式。

用图神经网络体验一把发现牛顿运动定律的快感

为了验证我们的方法，我们首先生成了一系列的 二维和三维的力学模拟。

 

我们对 GNN 进行模拟训练，并尝试从每个 GNN 中提取解析表达式。然后我们检查消息特征是否等于真正的力向量。最后，我们将符号回归应用到 GNN 内部的消息函数中，看看是否可以在没有先验知识的情况下还原力学规律。

 

               

消息的稀疏性显示了它对于提取正确表达式的重要性。如果不鼓励消息中的稀疏性，GNN 似乎会对消息中的冗余信息进行编码。随着时间的推移，训练过程显示出稀疏性鼓励信息函数变得更像一个力学公式:

把GNN用到天体物理学中，奇迹发生了！

如果把这种方法应用到天体物理学中，会有什么奇迹发生吗？我们用GNN来探究一下宇宙学中的暗物质，暗物质本身占宇宙总物质的85% (Spergel 等，2003)。

 

宇宙各种物质和能量的相互作用，推动了星系和恒星等复杂结构的演化。暗物质促进了星系的发展， 暗物质粒子聚集在一起，形成称为「暗物质晕」的引力盆地，将规则的物质拉到一起产生恒星，并形成更大的结构，如丝状体和星系。

               

宇宙学的一个重要挑战是根据暗物质晕周围的「晕」来推断暗物质晕的性质。在这里，我们研究的问题是: 如何只使用它的性质和它的邻近晕的性质，来预测晕的超密度？

 

我们采用相同的 GNN 模型，只是现在我们预测的是晕的超密度而不是粒子的瞬时加速度。图中每个晕都与半径为50 mpc / h （距离单位）的晕有联系。GNN准确地学习了这个关系，击败了以下手工设计的模型:

     

其中 ri 是位置，mi 是质量， Ci 是常数。

 

经过检查，在这个 GNN 中传递的消息只有一个重要的特性，这意味着 GNN 已经知道它只需要对相邻的函数求和(很像手工设计的公式)。然后我们拟合节点函数和消息函数，每个节点都输出一个标量，并找到一个新的解析方程来描述给定环境下暗物质的超密度:

       

GNN推出来的平均绝对误差仅0.088，而手工制作的方程平均绝对误差是0.12。 值得注意的是，我们的算法已经发现了一个比科学家设计的更好的解析方程式。

 

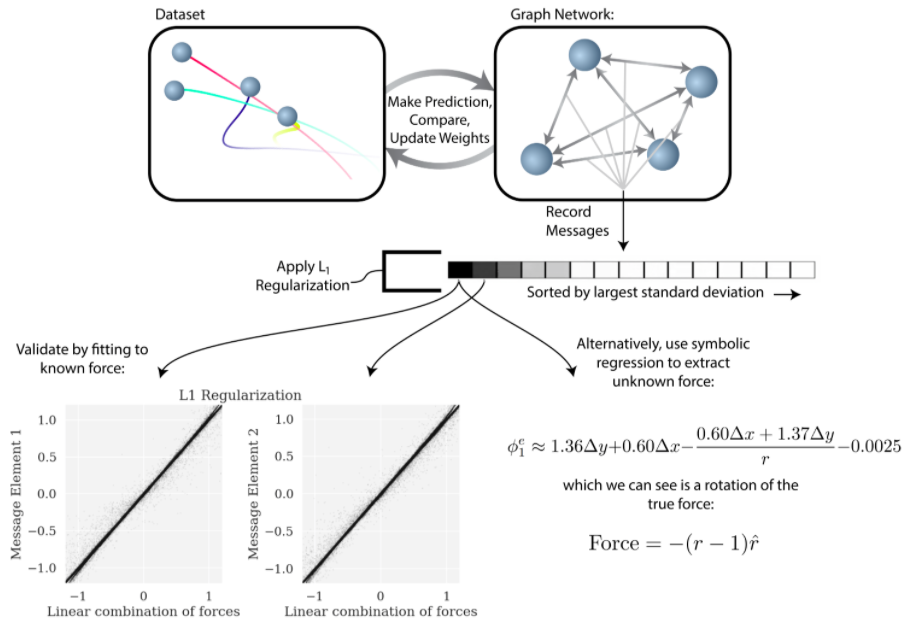
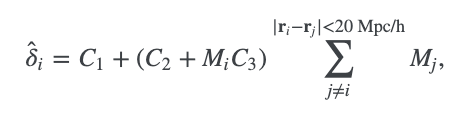
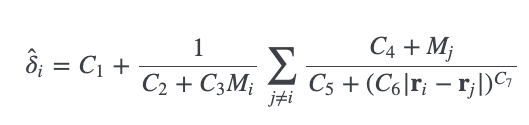
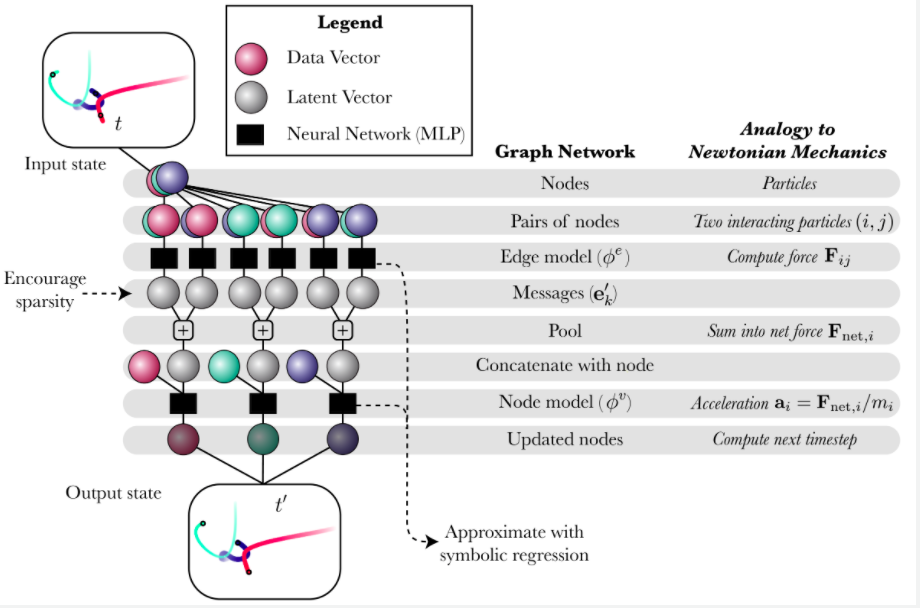
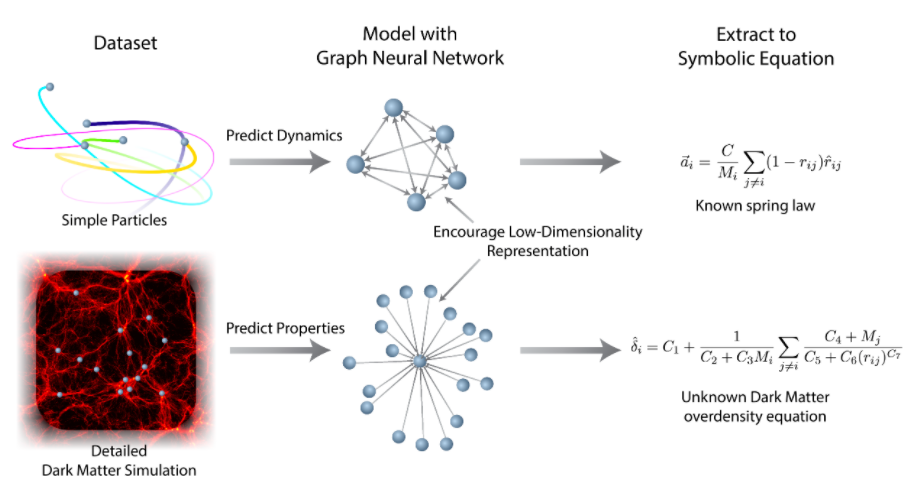           一个神经网络经历监督式学习，然后符号回归接近模型的内部函数

 

结论：符号表达式比图神经网络更稳定

有趣的是，当我们当掩盖20% 的数据进行相同的训练后，从这个子数据集的图形网络中提取到了一个功能相同的表达式。

 

然后，我们比较了 GNN 和符号表达式的泛化效果。图形网络本身在训练集上得到的平均误差为0.0634，在非分布数据上得到的平均误差为0.142。而符号表达式在训练集上达到0.0811，在非分布数据上达到0.0892，泛化能力相当稳定！

 

因此，对于这个问题， 符号表达式的概括能力比图神经网络要好得多 。结果又回到了尤金 · 维格纳的文章:「 仅用简单的符号语言就能有效地描述宇宙」。

 

本文作者是普林斯顿大学的博士，他一直在尝试用AI来加速天体物理学的发展。     

你如果感兴趣可以去作者的GitHub找到论文的源码，亲自体验一下发现物理定律的快感！

 

参考链接：

https://github.com/MilesCranmer/symbolic_deep_learning

https://blogs.scientificamerican.com/cross-check/troublemaker-lee-smolin-says-physics-8211-and-its-laws-8211-must-evolve/

https://astroautomata.com/paper/symbolic-neural-nets/

https://arxiv.org/pdf/2006.11287.pdf