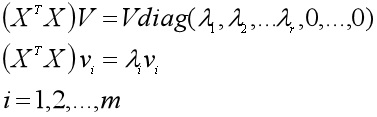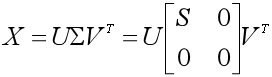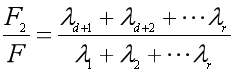奇异值分解：协同过滤的前奏，你是SVD（上）

一 ：内容预告

最近在看机器阅读理解的模型，学到了双向注意流网络（BiDAF），模型的细节太复杂了，让我产生了厌学情绪。

所以这周没写新东西，还是发一篇旧文，关于奇异值分解（Singular Value Decomposition，SVD）。

奇异值分解是一种非常重要的降维方法，主成分分析法（PCA）、潜在语义分析（LSA）和协同过滤（CF）都用到了奇异值分解。

这篇文章以数学推导为主，一步步搞清楚奇异值分解是什么。当然相信我，这些推导比较简单。

本文关注以下问题：

1：奇异值分解的数学公式；

2：奇异值分解的流程总结和案例；

3：用奇异值分解进行降维；

4：特征分解、奇异值分解和主成分分析法的关系；

5：奇异值分解在词向量降维中的应用。

二：奇异值分解的数学公式

一个n×m的矩阵X，其奇异值分解定义为：

其中U称为左奇异矩阵，是一个n×n的正交矩阵，即满足U^TU=E，U^T=U^-1。

而V称为右奇异矩阵，是一个m×m的正交矩阵。

Σ为n×m的对角矩阵，对角线上的非零元素是奇异值（Singular Value）。

01

求奇异值

首先看 Σ或者说奇异值是什么。

如果矩阵X的秩rank(A)=r，那么实对称矩阵X ^T X与X的秩相等，X ^T X有r个非零的特征值和m-r个零特征值： λ ₁ ≥λ ₂ ≥ λ ₃ ...≥λ _r >λ _r+1 =...=λ _m =0。

奇异值σ为：

矩阵Σ可以表示为（diag表示对角矩阵）：

02

求右奇异矩阵V

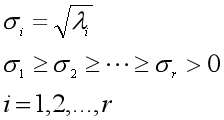
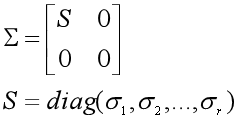
然后看右奇异矩阵V是什么。

将V写成列向量的形式（v₁, v₂, ...v_r,... v_m），那么V的列向量是实对称矩阵X^TX的单位特征向量，也就是有：

03

求左奇异矩阵U

（一）第一种做法

第一种做法更多是为了与右奇异矩阵V的求法相对应，实际计算时会采用另外的方法。

如果实对称矩阵X^TX与X的秩相等，有r个非零特征值，那么另一个实对称矩阵XX^T与X^TX的秩相等，同样有r个非零特征值，且这两个矩阵的非零特征值相等。

将U也写成列向量的形式（u₁, u₂, ...u_r,.. u_n），那么U的列向量是实对称矩阵XX^T的单位特征向量，也就是有：

看到这里，虽然不知道这是怎么推导过来的，但是感受到了一种强烈的数学之美，有没有！

（二）第二种做法

在第二种做法中，我们会充分利用实对称矩阵X^TX与右奇异矩阵V，来求得左奇异矩阵U，而不用另外去求XX^T的单位特征向量。

我们首先把X^TX的特征值分为两组：

特征值大于零的一组（r个），特征值等于零的一组（m-r个）。

相应的把右奇异矩阵的列向量分为两组：

前r个非零特征值对应的单位特征向量为V₁=(v₁, v₂, ...v_r)，而零特征值对应的单位特征向量为V₂=(v_r+1,.. v_m)。

再把左奇异矩阵U的列向量也分为两组，尽管我们还不知道具体的元素值，但是我们知道它有n个列向量：前r个列向量U₁=(u₁, u₂, ...u_r)，后n-r个列向量U₂=(u_r+1, u_r+2, ...u_n)。

那么我们可以用X、V₁和奇异值构成的对角阵方阵S来求出U₁。

由第一种做法我们已知U₁是XX^T非零特征值的单位特征向量，那么U₂就是零特征值的单位特征向量了。

我们不用去求U₂，只要构造n-r个列向量，每一个列向量满足：

与其他n-1个列向量正交，且是单位向量 ——这通常是比较容易构造的。

于是我们就得到了左奇异矩阵U=(U₁, U₂)。

我们还可以证明，由XV₁S^-1所得到的U₁的确满足： 列向量相互正交且为单位向量。

这个证明很有用，并不复杂。

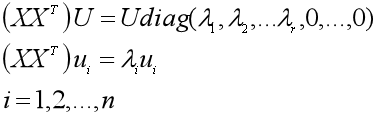
三：计算流程和案例

根据第一 部分的内容，尽管我们不知道怎么推导，但已经知道如何进行奇异值分解了。

01

奇异值分解的计算流程

如果有一个n×m的矩阵X，秩为r，那么对X进行奇异值分解的一种做法是：

^{（1）求出实对称矩阵XTX的m个特征值λ_i（其中非零的有r个）和m个单位特征向量v_i；}

（2）把m个特征值λ_i从大到小排序，求出奇异值σ_i=√λ_i（i=1,...,r），并得到S=diag(σ₁,σ₂,...,σ_r)；

（3）相应地把m个特征向量v_i进行排列，就可以得到右奇异矩阵V=（v₁, v₂, ...v_r,.. v_m），同时得到非零特征值的特征向量矩阵V₁=(v₁, v₂, ...v_r)；

（4）由XV₁S^-1求出n×r的矩阵U₁，写成U₁=(u₁, u₂, ...u_r)；

（5）构造n-r个列向量u_i，每个都满足与其他n-1个列向量正交且是单位向量的条件，写成U₂=(u_r+1, u_r+2, ...u_n)，于是得到左奇异矩阵U=(U₁, U₂)=(u₁, u₂, ... u_r, ..., u_n)；

（6）得到X的奇异值分解：

接下来我们就举一个简单的例子，按这个流程走一遍。

02

奇异值分解的案例

问题：

对以下的矩阵X进行奇异值分解。

求解：

四：奇异值分解降维

用奇异值分解进行降维，需要用到线性代数里的分块矩阵理论。

01

简化奇异值分解

可以看到，矩阵Σ由奇异值和很多0元素构成，强迫症的我看到这些0元素比较难受，尤其是对角线上的！

所幸我们可以用矩阵分块的方法，把Σ中为0的对角元素抛弃。

同样，X是n×m的矩阵，右奇异矩阵V中的前r个列向量为V₁=(v₁, v₂, ...v_r)，左奇异矩阵U中的前r个列向量为U₁=(u₁, u₂, ...u_r)，S=diag(σ₁,σ₂,...,σ_r)是奇异值构成的对角矩阵。

则可以将奇异值分解化简为X=U₁SV₁^T。

02

奇异值分解降维

我们是用分块矩阵对奇异值分解进行化简的，现在让我们分块到底！

我们知道U₁中有r个列向量，我们再将其分块，比如我们想把维度降到d维（d<r），那么把U₁分为两个子矩阵U₁=[U₁₁, U₁₂]，有U₁₁=[u₁,u₂,...,u_d]，U₁₂=[u_d+1,u_d+2,...,u_r]。

同样把V₁进行分块，得到V₁=[V₁₁, V₁₂]，V₁₁=[v₁,v₂,...,v_d]，V₁₂=[v_d+1,v_d+2,...,v_r]。

于是我们可以把X=U₁SV₁^T也分块成：

因此如果我们想把维度降到d维，那么就让X≈U₁₁S₁V₁₁^T。

这样我们就舍弃了r-d维的信息U₁₂S₂V₁₂^T，那不免让人担心，信息是否会损失太多。

所以如何计算损失的信息量呢？

03

信息量度量

主成分分析法的文章提到了，可以用数据集的方差来衡量数据所包含的信息量的大小，方差越大，包含的信息越多。

而方差又和特征值密切相关，在某些特殊情况下方差就等于特征值。

于是我们隐约感觉到，可以用奇异值或者特征值来度量矩阵的信息量。

是的，矩阵X的信息量就定义为所有奇异值的平方和，也就是X^TX的特征值之和：F=λ₁+λ₂+…+λ_r

那么降维后的矩阵U₁₁S₁V₁₁^T的信息量为：

F₁=λ₁+λ₂+…+λ_d

而损失的信息为矩阵U₁₂S₂V₁₂^T的信息量：

F₂=λ_d+1+λ_d+2+…+λ_r

于是损失的信息量占总信息量的比例为：

这样我们就可以清晰地看到，降至d维后，信息量是否损失太大，是否让我们无法承受。

不过好在S中的奇异值是降序排列的，而且数值一般下降得特别快，前面少数几个奇异值的平方和占总信息量的比例一般就已经很大了。

好，到这里我们就明白了，怎么度量降维后的矩阵所包含的信息量。

然后，作为好奇宝宝的你也许会问，为什么矩阵X的信息量就是所有奇异值的平方和呢？

好的，邓紫棋已经听到你的呼唤了，返场唱最后一首歌。

这里是用矩阵X的F范数的平方来度量信息量。

什么是矩阵的F范数呢？

矩阵的F范数定义为矩阵中每个元素平方之和的平方根，那么F范数的平方就是每个元素的平方和。

因为矩阵X每个元素的平方和（F范数的平方）是方阵X^TX的对角线元素之和（迹），而方阵X^TX的对角线元素之和（迹）就是其特征值之和，也就是奇异值的平方和。

所以矩阵X的信息量就是所有奇异值的平方和。

下一篇介绍奇异值分解和主成分分析法的关系，以及奇异值分解在词向量降维中的应用。

参考资料：

1、《A Tutorial on Principal Component Analysis. Derivation, Discussion and Singular Value Decomposition》

2、《A Singularly Valuable Decomposition: The SVD of a Matrix 》

END

推荐阅读

AINLP年度阅读收藏清单

百度PaddleHub&nbsp;NLP模型全面升级，推理性能提升50%以上

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

From Word Embeddings To Document Distances 阅读笔记

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

可解释性论文阅读笔记1-Tree Regularization

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。