商业化广告策略解读

会员服务 ·

商业化广告策略解读

2020 年 5 月 19 日 DataFunTalk

分享嘉宾：莫菲克

编辑整理：Hoh

内容来源：莫菲克@知乎

出品平台：DataFunTalk

注：转载请在公众号后台回复“转载”。

导读：随着互联网的高速发展，在线广告的市场规模水涨船高，成为互联网主流的变现模式之一，也催生了一批广告巨头，如国外的Google、Facebook，国内的字节跳动、阿里、百度、腾讯，广告在整个营收中占据着重要的位置。

前文中，我们介绍了广告动态化、目标转化出价、数据管理平台 ( DMP )、广告的拍卖内核、机制设计、最优机制等方面。详情请参考：

商业化广告策略随笔

今天将为大家分享最优机制的经济学解释、市场保留价、动态保留价、价格挤压因子、预算消耗控制等内容。

最优机制的经济学解释

在最优机制的介绍中，我们构造了常规问题下买家的一个虚拟估价函数：

其中 v 是估价，Y 是虚拟估价，满足正则假设则 Y 关于 v 单调递增，并选择分配规则是虚拟估价最高者得，支付规则是二价计费，假设买家 i 的虚拟估价最高，则获得拍卖品，除买家 i 以外虚拟估价最高值记为 Y_-i，令 Y_-i=A，那么此时买家 i 的支付为：

T_i=Y^-1(A)

其中 Y^-1 是买家 i 虚拟估价函数的反函数，我们称该机制是不带保留价的最优机制，此时卖家的期望收入最大化，接下来我们展开讲一下为什么卖家要按照买家的虚拟估价竞价，虚拟估价在经济学中又有什么含义。

假设卖家为一个买家制定了一个价格为 p 的接受-拒绝方案，此时 F(p) 是买家估值小于 p 时的概率，则买家估值大于 p 的概率为 1-F(p)，即买家接受方案获得物品的概率，其中 F 是买家估值的累积分布函数，此时把买家接受方案获得物品的概率看做买家的需求数量，可得需求数量与价格的函数关系式如下：

q(p)=1-F(p)

上述是经济学中的需求函数：在不同的价格下，买家的需求数量不同，且单调递减，需求曲线斜率为负，它的反函数为：

p(q)=F^-1(1-q)

则卖家的收益函数：

TR=p*q=F^-1(1-q)*q

对总收益 TR 关于数量 q 求导，把 F^-1(1-q)=p 带入后可得：

此时可以发现，边际收益函数式 MR(p) 和买家的虚拟估价函数式 Y(v) 相同，即买家的虚拟估价是卖家的边际收益，经济学中边际收益是指卖家每增加一单位产品的销售所增加的收益，在一次不可分割的单品拍卖中，当前卖家的收益就是就是边际收益，为获得收益最大化，卖家选择的分配规则是把拍卖品分配给虚拟估价最高者，支付规则选择二价计费是为了减少买家报价的波动性，有利于拍卖系统的稳定。

在现实拍卖中，卖家不一定会把拍卖品卖给虚拟估价最高的买家，只有当最高虚拟估价 Y 大于等于卖家对拍卖品的估价时才会出售，这点其实很容易理解：卖家只有在收益大于等于成本时才会发生交易，此时卖家对物品的估价就是成本，这里就引出拍卖的另一个概念：保留价，顾名思义当买家报价小于该价格时卖家保留拍卖品，下节我们展开聊。

市场保留价

刚刚我们提到在一次拍卖中如果所有买家的报价均小于卖家的估价时，则拍卖品不出售由卖家保留，此时卖家的估价就是保留价，也叫底价，全称市场保留价，下面我们展开讲一下。

1. 卖家设置保留价的原因是什么？

不想亏本

对于卖家而言拍卖的东西本身具有一定的价值 ( 成本 c )，如果在低于该价值的价格出售 ( p )，则此时卖家的效用：

u=p-c＜0

基于个人理性假设，卖家此时选择保留拍卖品，这里引出拍卖的一个基本假设：个人理性，当拍卖双方都不参与拍卖时，收益为 0，支出为 0，效用：

u = 0 - 0 = 0

发生拍卖的前提条件是对所有参与人都有利可图，即 u_i≥0。

另一个基本假设是在机制设计里提到过的激励兼容 ( 说真话保障广告系统的持续发展 )。

为了增加拍卖时竞价环境的激烈程度，保障卖家收益。

尤其是在合作博弈中，买者之间存在合谋 ( 竞价环 )，通过合作不断降低报价增加了环中的买家收益，环的运作不会影响环外买家的获得物品的概率函数及期望支付，环中增加的收益来自卖家的损失，此时卖家可以借助保留价的机制来对抗竞价环。

2. 设置保留价对拍卖的整体的影响是什么？

拍卖可能不再有效

设置保留价后卖家可能会保留拍卖品，没有分配给估价最高的买家，此时拍卖不再有效，影响了拍卖的社会效应，当然如果是基于私有价值的拍卖那么不会有太多人在意；

竞得者的支付函数可能发生变化

当只有一名买家的报价高于保留价时，在广义二价中，保留价将会改变获胜者的支付价格，假设买家 i 报价 b_i：

b_i＞b_j≠i，且 b_i≥r

除获胜者以外最高报价记为：

maxb_j≠i=b_-i＜r

没有保留价时胜者支付：

p_i=b_-i

有保留价时则支付：

p_i=MAX(b_-i,r)

此时卖家收益增加。

3. 保留价有诸多好处，卖家在具体某次拍卖中如何设置保留价？

定价太高则拍卖品卖不出去，此时卖家效用为 u=0；定价太低在竞价不充分时则买家 i 可能以很低的价格获得物品，此时卖家效用 u 没有达到预期。

对于广告系统而言，粗一些的做法是根据广告主们的历史竞价情况，取一个使填充率没有明显下降的固定值作为保留价，相对比较简单，一定程度上也可以防止广告主无限下探出价，降低平台收益；精细一些就是针对不同广告主设置不同的动态底价，这对数据和模型的要求比较高，当然广告平台的收益也会相应增加，有本事多赚钱的道理，计算方法涉及到我们在最优机制里提过的虚拟估价，具体细节我们下节聊。

动态保留价

在拍卖中卖家为了增加拍卖竞价环境的激烈程度，保障收益，设置了保留价，对于广告平台而言，有众多广告主参与竞价，统一设置固定的保留价则不能使平台收益最优，为此提出动态保留价，下面我们展开讲一讲。

从计算上讲，动态保留价与固定保留价相比，主要差别在于针对不同的广告主设置不同的价格上，更加精细，千人千面就需要了解广告主的特性及对广告曝光的估价分布。在最优机制里，我们提出最优机制的拍卖时竞价的标准不是广告主估价而是虚拟估价，并且解释了为什么使用虚拟估价代替估价的经济学解释，它代表了卖家的边际收益，在一次单品拍卖中把物品配置给边际收益最高者，里面有个隐含假设：

最高的虚拟估价高于保留价，即：

Y≥V₀=r

其中，V₀代表卖家对物品的估价，即保留价 r，同时也是卖家的成本。

在求动态保留价时，我们令 Y=r，即：

v-(1-F)/f=r

解出上式中的 v^*，就得到针对该买家的动态保留价，从上式可以看出要解出等式必须知道 f(v)，即买家估价的密度函数，这个前提与最优机制时是一致的：

不知道各个买家的估价分布无法针对性的设置保留价和最优机制来最大化卖家收益。

这里可能会有个疑问为什么令 Y=r，解出来的 v^* 就代表了动态保留价，下面我们说下经济学的解释。

从经济学角度，随着物品供给量不断增加时，边际收益递减，边际成本递增，当

MR=MC

企业利润最大化。在单品拍卖中，虚拟估价 Y 代表边际收益，保留价 r 代表边际成本，令 Y=r ，即：

Y=MR=MC=r

此时卖家利润最大。

又因为广告拍卖的是曝光，有区别与其他拍卖品，不能长期储存，过后即废，所以在实际操作中有时令 r=MC=0，此时上式变为：

v-(1-F)/f=0

即 v^*=(1-F)/f 可得买家的动态保留价。

下面我们用图可以更加直观的感受下：

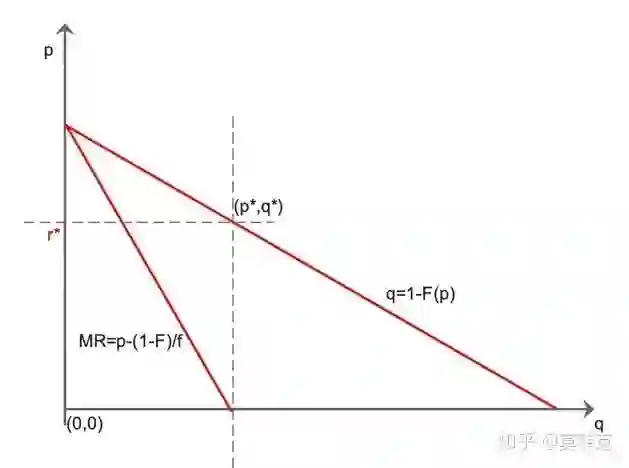
其中，q=1-F(p)，代表需求函数，MR=p-(1-F)/f，代表边际收益函数 ( 也是买家的虚拟估价函数 )。

当 MR=0 时，得到最优产量及价格 (p^*,q^*) , 此时 p^* 对应上面的动态保留价 r^*。

对于广告系统而言，不同广告主有不同的估价，需要根据历史数据拟合出估价分布函数，基于此求出广告主各自的保留价后分别设置。

这里我们可以完善下关于之前对最优机制的描述：

分配规则：当 maxY≥r 时，虚拟估价最高者得，否则保留物品；其中 Y 表示买家的虚拟估价；
支付规则：竞得者需支付价为 Z，Z=max(Y^-1(A),r^*)
其中 A=Y_-i，表示除去竞得者买家 i 的虚拟估价最高者， Y^-1 表示买家 i 虚拟估价的反函数，r^*=Y^-1(0)

如果买家是对称的，此时 f(i)=f

则：Z=max(maxX_j,Y^-1(0))

其中，maxX_j 表示除竞得者 i 以外的最高报价。

即带保留价为 r^*=Y^-1(0) 的二价拍卖为最优拍卖机制。

价格挤压因子

广告作为一种特殊的拍卖继承了拍卖的内核，还发展出一些特色，比如作为拍卖品的曝光不易存储过期即废，比如出价最高者未必会赢得拍卖，这就涉及到广告竞价的特殊逻辑。

竞价广告起初按照千次展示 ( cpm ) 出价，出价最高者获得曝光，后来在效果类广告主的推动下，出价向后延伸，发展出按点击 ( cpc ) 出价，分配规则还是出价高者得，此时对广告平台/媒体不利 ( 相当于免费给出价高但点击低的广告主宣传 )，后来Google 把点击率引入竞价公式，将出价与竞价分割开来，竞价的标准变为 ecpm，这是一次重大创新，价高者得具化为 ecpm 高者得，ecpm 不仅包含了经济维度的出价，还包括了广告质量维度的内容和用户契合程度，综合考虑了广告主、平台、和用户。对于按照点击出价的广告，计算公式如下：

ecpm=1000*pCTR*bid_c

其中， pCTR 是预估点击率，bid_c 是广告主的点击出价。广告主想赢得曝光，就要尽可能提高 ecpm，主要着力点是 pCTR 和 bid_c， pCTR 受三方面影响：广告、用户、广告场景 ( 上下文 )，出价主要受广告主估价的影响。

广告平台在实际的运行中会面临不同的情况和诉求，比如媒体反馈广告质量差，影响用户体验；广告主下调出价或者数量减少导致竞价环境下降，影响平台收益。平台希望有一定的操作空间来影响竞价结果，这就引出了价格挤压因子 p，通过挤压因子平台能够有效平衡质量与收入，加入挤压因子后的竞价公式如下：

ecpm=1000*pCTR^p*bid_c

其中 p＞0，0＜pCTR＜1，bid_c＞r，r 为保留价。

通过公式可以得出以下结论：

当 p 值逐渐增大时，点击率在 ecpm 中的权重会增大，价格的权重会减少，对 ecpm 的影响被挤压出去，这也是 p 被称为价格挤压因子的原因；
当 p 值逐渐减小时，点击率在 ecpm 中的权重会减少，价格的影响力会不断提升。

平台会在什么场景下调整 p 值及如何调整？

当竞价环境降低收益下降时，平台可以降低 p 值，加大价格权重，此时广告主下调出价， ecpm 下降的比例会大于出价下调的比例，导致广告主拿量加速下滑，因为是采用二价计费，作为理性人广告主会停止降价进而提价，提价后拿量上升的比例大于实际成本增加的比例，鼓励平台广告主持续提价，最终改善整体竞价环境。

当反馈广告质量差，影响用户体验时，出于长久考虑，平台可以提高 p 值，加大点击率权重，此时广告主发现提高出价增加曝光的效果远不如通过优化素材提升点击率带来的曝光效果，作为理性人，广告主会持续优化素材提升创意质量，最终优化了用户体验。

上面说的是挤压因子对分配规则的影响，对竞得者的支付影响如下，在二价计费中竞得者的实际支付 T_i 如下所示：

T_i=ecpm_n+1/(1000*pCTR^p)

计费价格始终小于出价。

广告平台在业务长期发展中探索出了一套有效的工具集，各有神通，通过运用以引导趋势朝着期望的方向发展，挤压因子就是其中一柄利器，广告生态的规模越大，效果就越显著，工具集其他成员我们后续再聊。

预算消耗控制

广告平台希望有越来越多的广告主参与投放，供不应求会提升竞价环境，平台收益自然水涨船高，这里有个前提：有足够大的流量盘子来满足不同广告主的多样化投放诉求。凡事有利有弊，流量大随之而来的一个问题：

中小广告主每天预算是有限额的，按照 ecpm 排序分配流量，则很多广告主会短时间内快速消耗完预算停止竞价，只能等新周期开始才能重新参与。

有没有方案可以有效解决这个问题，由此引出了一个平台工具：预算消耗控制 ( Budget pacing )，下面我们展开聊聊。

预算消耗控制的意义是什么，主要从三个维度来阐述。

1. 广告主

希望预算可以在一天中平滑消耗 ( Smooth delivery )，计划的生命周期足够长，从而触达不同时段的用户。

2. 平台

希望在一天中后期能够维持前期的竞价环境，尤其对于二价计费，如果中后期参竞者显著减少，会在很大程度上影响收益；
消耗数据的滞后性导致广告超跑，这在一定程度上不可避免，通过预算消耗控制可以减轻超跑情况。

3. 用户

不希望一天内频繁出现重复广告，减少重复率，提升体验。

基于上述考虑现提出解决思路以控制预算消耗，主流有两个方向：

调整参竞率
通过调整参与竞价的概率来影响广告参与竞价的次数，消耗快了则降低概率，消耗慢了则提高概率。
调整竞得率
通过修改出价来影响广告获胜的次数，消耗快了则降低出价，消耗慢了则提高出价。

对于修改出价影响竞得率的思路，有以下几个问题需要考虑：

竞价环境随时在变，调整当前广告出价后，大盘竞价环境可能同时发生变化，竞得率可能没有按照预设的方向发展；
SSP 部分位置可能会设置底价，如果需要降低的出价小于底价则无法拿量，一定程度上限制调价的空间；
将预算消耗控制和优化 ROI 耦合在一起，一个行为关联多个目标可能会互相制约。

综上所述建议使用调整参竞率来控制预算消耗速度，调整参竞率也有多种实现，下面我们介绍 LinkedIn 使用的方法。

LinkedIn 预算消耗控制方法

基本思路：通过调整参竞率使得广告计划 ( campaign ) 的预算消耗曲线与该计划获得的曝光曲线在比例上尽可能保持一致 ( 预算控制一般在计划层级 )，消耗快于曝光降低参竞率，慢于曝光提升参竞率。

根据计划 j 的历史数据，预估出计划在当天获得的流量分布，把一天分为 k 个时间片，日预算为 B_j ( 广告主设定 )，计划在各时间片的流量分布 :

I=(i₁、i₂、i₃、i₄ ... i_k)

按照比例分配预算：

B_j =(b₁、b₂、b₃、b₄ ... b_k)

其中 b_t≥0，；

F_jt 是预估出来从0:00开始到时间片 t 前的累计曝光量，；

F_jk 是一天的累计预估总曝光量，；

S_jt 是从0:00开始到时间片 t 前的累计实际消耗；

A_jt 是从0:00开始到时间片 t 前的累计计划消耗，则：

A_jt=F_jt/F_jk*B_j

P_jt是在时间片 t 时的计划 j 的参竞率；

R 是调整因子；

当实际消耗高于计划消耗则下个时间片的参竞率在上个时间片参竞率基础上下调比例 R，当实际消耗低于计划消耗则下个时间片的参竞率在上个时间片参竞率基础上上调比例 R，即：

P_jt=P_jt-1*(1-R)，S_jt≥A_jt

P_jt=P_jt-1*(1+R)，S_jt＜A_jt

关于上述算法中初始值设定需要注意几点：

时间片

长度设为为 1-3 mins ，时间片跨度越短则消耗曲线更加平滑，计算也越频繁。

初始参竞率 P_j1

P_j1=0.1，低速开始，给模型充足的学习时间，即使对某些计划初始参竞率低了可以通过快速迭代接近合理值，如果初始定的太高，可能造成没来及调整预算已经消耗完的情况。

调整因子 R

R=0.1，复杂的计算方法是针对 S_jt/t 求导计算。

周期长度

一天总时长按照 22h 来估计，为预防模型出错通过最后两小时来缓冲。

在整个反馈控制中，关键点是对流量的预测，决定了预算分配曲线，需要先预测计划j的定向目标人群的流量分布，结合计划的历史竞得率得到计划的流量分布。

以上是 LinkedIn 使用的预算消耗控制方法，思路简单但结果有效，后面我们再聊其他控制方法。

Yahoo 预算消耗控制方法

刚刚提到的关于 LinkedIn 的论文，通过动态调整参竞率来控制预算消耗速度。其基本思想如下：

计算实际累计消耗和计划累计消耗，实际消耗大于计划则降低参竞率，小于计划则提升参竞率，每次目标请求发起时通过概率丢弃部分广告请求。

上述方法中的这种丢弃是随机的，是否有方法可以根据请求的质量度来判断是否丢弃，当高质量请求 ( 高转化 ) 时参与竞价，低质量请求时丢弃，这样既可以控制消耗速度，同时可以优化效果，提升 ROI，这就引出下面我们介绍的 Yahoo 一篇论文中介绍的方法。

基本思想：

根据广告效果(比如点击率)将广告请求划分多个层，各层参竞率不同，点击率高的层参竞率高，点击率低的层参竞率低。当目标请求发起时，根据点击率预估模型落到具体某个层，并根据该层的参竞率来参与竞价。下一个时间片如果需要增加消耗则从最高层起依次向下增加参竞率，如果需要降低消耗则从参竞率大于0所在层起依次向上降低参竞率，始终保持实际消耗曲线贴近计划消耗曲线以达到预算平滑消耗的效果。

具体实现逻辑我们稍微展开说一下，基本设定如下：

根据历史数据制定计划预算消耗 B，一天时间切分为 K 份：

B=(B₁、B₂、B₃... b_k)

其中，B_i≥0，，B^m 是经过 m 个时间片以后实际剩余的预算，一天内实际消耗：

C=(C₁、C₂、C₃... C_k)

根据转化目标不同的值把计划的目标请求分成 L 层，假设目标取点击率，则各层点击率如下：

S=(S¹、S²、S³... S^L)

点击成本：

E=(e¹、e²、e³... e^L)

t-1 时间片时各层的参竞率：

R_t-1=(r_t-1¹、r_t-1²... r_t-1^L)

t-1 时间片时各层实际消耗：

C_t-1=(C_t-1¹、C_t-1²... C_t-1^L)

则时间片 t 的调整后的消耗应该为：

其中，表示经过 t-1 时间片以后计划与实际消耗之间的差额；

表示把差额平摊到后续的各个时间片里。

令 F=C_t-C_t-1 代表相邻两个时间片的消耗差值。根据 F 的值分情况来计算确定时间片 t 内各层的参竞率。

说明t时间片的调整后消耗与 t-1 时间片的实际消耗一致，继续使用上一时间内的各层的参竞率不用调整即：

R_t=R_t-1=(r_t-1¹、r_t-1²... r_t-1^L)

F＞0

说明时间片 t 的消耗要大于 t-1，此时需要提升参竞率，直至多出来的增加消耗完为止，参竞率从最高层 L 逐层往下提升参竞率 (上层的点击率更高 )，各层在 t 的参竞率 r_t^L 计算公式如下所示：

r_t^L=min(1,r_t-1^L*(c_t-1^L+F)/c_t-1^L)

F=F-c_t-1^L*(r_t^L-r_t-1^L)/r_t-1^L

直至 F=0 为止；

F＜0

说明时间片 t 的消耗要小于 t-1 的实际消耗，此时需要降低参竞率，直至差额抵消完为止，参竞率从低层 l ( 参竞率非0的最小所在层 ) 逐层往上降低参竞率 ( 下层的点击率更低 )，各层参竞率 r_t^L 计算公式如下所示：

r_t^L=max(0,r_t-1^L*(c_t-1^L+F)/c_t_-1^L

F=F-c_t-1^L*(r_t^L-r_t-1^L)/r_t-1^L

直至 F=0 为止。

在实际中可以根据 F 具体的值采用不同的计算公式算出时间片 t 内的各层参竞率。

例子：如在第3个时间片内，目标用户发起一次广告请求，模型预估点击率 pCTR=3%，共有5层，第2层的点击率区间为[0.02，0.04]，则此次请求落在第二层，该层的参竞率 r₃²=30%，划分区间[0,29]和[30-99]，随机数生成是28则参与此次竞价，生成随机数是45则放弃该次请求，不参与竞价。

有约束条件下的预算消耗控制

刚刚提出的将广告请求分层的想法，基本思路是各层按照不同的参竞率来参与竞价，从而实现控制预算消耗的速度，同时有效提升广告效果。

这里面有个前提，广告计划没有明确的效果约束条件，如果有该如何处理，Yahoo 的论文针对这种情况提出了一种探索性解决方案，下面我们展开聊聊。

假设与前文中保持一致，包括预算分配、时间划分、请求分层、前后时间片消耗差额等。在此基础上，增加了如下假设：

广告按照 cpm 出价，效果目标是 cpc 价格不能高于某个阈值 ( goal )；

这点好理解，从转化路径上讲，效果目标约束在出价之后，否则直接通过出价来控制效果就可以。

提出分层累加 ecpc(C_t-1,R_t-1,R_t,E,i) 概念，代表从第 i 层到 L 层，在时间片 t 的累加 ecpc；

计算公式如下：

其中分子代表了时间片 t 内从 i 到 L 层的总消耗，分母代表了时间片 t 内从 i 到 L 层的总点击次数，二者相除可得从 i 到 L 层的

ecpc(C_t-1,R_t-1,R_t,E,i)

后面简称 ecpc(i) 。

下面介绍计算各层参竞率方法：

用前文中无约束算法得出各层参竞率：

R_t-1=(r_t-1¹、r_t-1²... r_t-1^L)

并计算 ecpc(1) ：

当 ecpc(1)≤goal，继续采用无约束算法；
当 ecpc(1)＞goal ，则采用下面算法获得各层参竞率：

从第一层开始循环，依次向上计算，i=1,2...L，ecpc(i)＞goal，计算ecpc(i+1)：

当ecpc(i+1)≥goal 时

第 i 层参竞率 r_tⁱ=0

当 ecpc(i+1)＜goal 时

其中, 代表 i+1 到 L 在消耗分别是：

c_t-1ⁱ⁺¹、c_t-1ⁱ⁺²... c_t-1^L时，小于目标成本累计的金额；

c_t-1ⁱ*(1-goal/e_i) 代表第 i 层消耗为 c_t-1ⁱ 时，大于成本的金额。

时间片 t 内 r_tⁱ 根据比例调整，如果＞1，提高参竞率，如果＜1，降低参竞率，最终使得 epc(i)=goal，满足目标约束。

这里有个假设：该层参竞率与消耗正相关。

新计划没有效果数据对于实验参数取值有如下建议：

根据相似度找出一个在跑老计划，找出一个能够使得预算消耗完的全局参竞率 r，

令层数 L=1/r；

在冷启动阶段所有层使用统一的参竞率，把获得曝光的请求数按照预估点击率排序并根据既定层数取相同数量，确定各层的点击率边界。

综上我们分别介绍了两种控制预算消耗的方法：

LinkedIn 方法实现简单，不用分层，根据实际累计消耗和计划累计消耗的关系来调整参竞率，虽然无法保证效果，但可以有效控制消耗速度；
Yahoo 的方法可以同时兼顾消耗速度和效果，但是模型相对复杂，尤其根据有无明确效果目标提出两种算法，增加了不少难度。

上述方案各有特色，适用场景也有所不同，具体运用需要根据实际情况加以判断。

本次的分享就到这里，谢谢大家。

作者介绍：

莫菲克，一个对广告有浓厚兴趣的广告从业者。

原文链接：

https://www.zhihu.com/people/mophic/posts

如果您喜欢本文，欢迎把文章分享到朋友圈~~

社群推荐：

欢迎加入 DataFunTalk 计算广告技术交流群，跟同行零距离交流。如想进群，请加逃课儿同学的微信 ( 微信号：DataFunTalker )，回复：计算广告，逃课儿会自动拉你进群。

文章推荐：

商业化广告策略随笔

Hulu：视频广告系统中的算法实践

关于我们：

DataFunTalk 专注于大数据、人工智能技术应用的分享与交流。发起于2017年，在北京、上海、深圳、杭州等城市举办超过100场线下沙龙、论坛及峰会，已邀请近500位专家和学者参与分享。其公众号 DataFunTalk 累计生产原创文章400+，百万+阅读，5万+精准粉丝。