科学和哲学之祖: 泰勒斯

米利都的泰勒斯，常被称为泰勒斯，是古希腊时期的哲学家和科学家，亦是希腊最早的前苏格拉底哲学学派之一，米利都学派（亦称爱奥尼亚学派）的创始人，希腊七贤之一，西方思想史上第一个有记载留下名字的思想家，被后人称为“科学和哲学之祖”。他的学生有阿那克西曼德和阿那克西米尼等。

节选自维基百科, [遇见数学] 有修改, 转载请注明. 

生平

泰勒斯出生于古希腊位于小亚细亚伊奥尼亚地区的繁荣港口城市米利都，父母是腓尼基人。他曾游历古埃及，跟当地祭司学习数学知识。根据希罗多德的《历史》记载，他准确预测到公元前585年5月28日发生的日全食。他能够估算船只离岸边的距离，解释尼罗河泛滥的原因，又能从金字塔的阴影计算出其高度。泰勒斯拒绝倚赖玄异或超自然因素来解释自然现象，对于科学研究影响深远，因而被历史学者尊称为“科学之父”。数学上的泰勒斯定理以他命名。他对天文学亦有研究，确认了小熊座，指出其有助于航海事业。同时，他是首个将一年的长度修定为365日的希腊人。他亦曾估量太阳及月球的大小，并确定分点与至点的时间。

泰勒斯试图借助经验观察和理性思维来解释世界。他提出了水的本原说，即“水是万物之本原”（Water is the arche），是古希腊第一个提出“什么是万物本原”这个哲学问题的人。

Thales雕塑自"The Progress of Railroading" (1908)，联合车站（华盛顿地区）的主立面

泰勒斯首创理性主义精神、唯物主义传统和普遍性原则，是理性主义的开端，被称为“哲学史上第一人”。他是个多神论者，认为世间充斥神灵。泰勒斯对希腊哲学产生了重要的影响，阿那克西曼德据说是他的学生，传说毕达哥拉斯早年也拜访过泰勒斯，并听从了他的劝告，前往埃及做研究。

理论

希腊人经常借用特殊的自然现象解释人格化的神和英雄。相反，泰勒斯旨在通过理性假说理解自然变化，解释自然现象。例如，泰勒斯解释说：地球漂浮在水中，地震是地球被海浪冲击导致的，而不是超自然的现象。

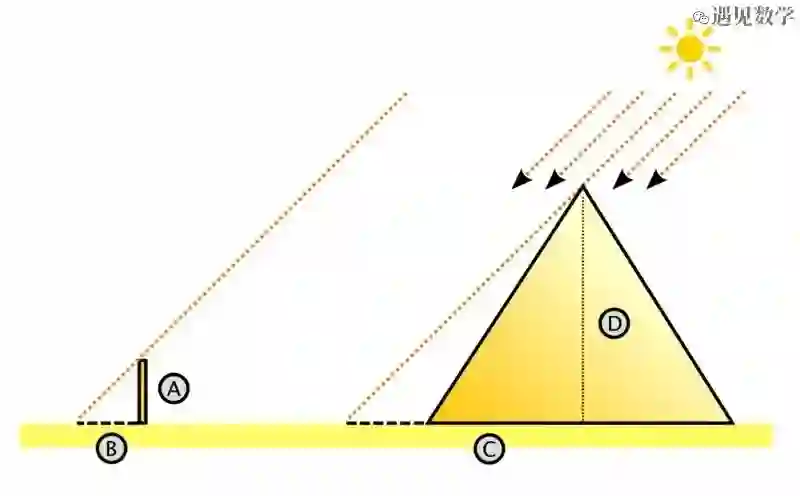
根据一些历史资料，希腊数学家泰勒斯应用截距定理来确定胡夫金字塔的高度。(具体见下节)

泰勒斯在数学方面的划时代贡献则是引入了命题证明的思想。在数学中引入了逻辑证明，以保证命题的正确性，并揭示各定理之间的内在联系，使古代数学开始发展成严密的体系。

泰勒斯定理(Thales' theorem)

泰勒斯定理（英语：Thales' theorem）以古希腊思想家、科学家、哲学家泰勒斯的名字命名，其内容为：若A, B, C是圆周上的三点，且AC是该圆的直径，那么∠ABC必然为直角。或者说，直径所对的圆周角是直角。该定理在欧几里得《几何原本》第三卷中被提到并证明。

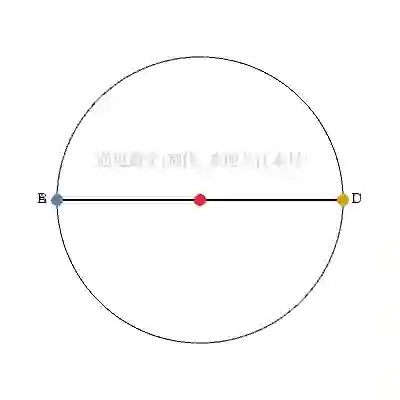
泰勒斯定理：如果AC是直径，那么∠ABC是直角。

泰勒斯定理的逆定理同样成立，即：直角三角形中，直角的顶点在以斜边为直径的圆上。

截线定理(Intercept theorem)

也称为泰勒斯定理（不要与混淆与上面同名的定理）或基本比例定理，是平面几何一个重要的定理。传统上它归功于希腊数学家泰勒斯。

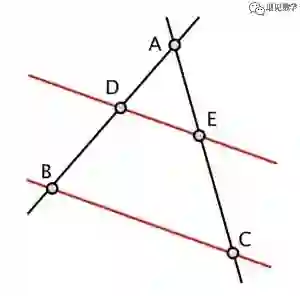
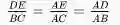
截线定理说明，平面上的一个三角形中，若在其中一条腰的中点作一条直线，与其底边平行，则该线穿过另一条腰的中点。这定理可推广到梯形上，以及一般化至任意分割比例的情况。截线定理与另外两条几何定理中点定理和等比定理有密切关系。

测量Cheops金字塔的高度

泰勒斯测量了金字塔底座的长度和杆的高度。然后在一天的同一时间，他测量了金字塔的阴影长度和杆的阴影的长度。这产生了以下数据：

杆的高度（A）：1.63米
杆的阴影（B）：2米
金字塔底座长度：230米
金字塔的影子：65米

由此计算出来 C=65 + 230/2=180 m

知道A，B和C他现在能够应用截距定理来计算
D=(C×A)/B=146.7m

测量河流的宽度

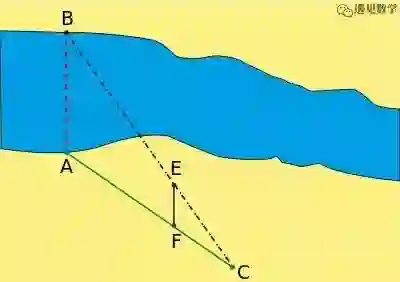
截距定理可用于确定不能直接测量的距离，例如河流或湖泊的宽度，高层建筑物的高度或类似物。右图显示了测量河流的宽度。如图所示 |CF|, |CA|, |FE| 都可以计算出距离, 这样就可以计算出河流宽度

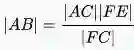
相关文章或视频

» 视频 | 米利都的泰勒斯