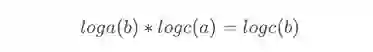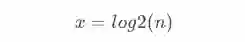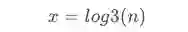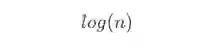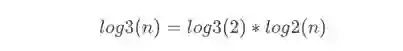时间复杂度的表示、分析、计算方法……一文带你看懂时间复杂度！

会员服务 ·

时间复杂度的表示、分析、计算方法……一文带你看懂时间复杂度！

2020 年 3 月 9 日 CSDN

作者 | OverRedMaple

责编 | Carol

来源 | CSDN 博客

封图 | CSDN付费下载于东方 IC

如果你还在发愁究竟怎么计算时间复杂度和空间复杂度，那你是来对地方了！

名词解释：

在计算机科学中，时间复杂性，又称时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。

时间复杂度的表示方法

其实就是算法（代码）的执行效率，算法代码的执行时间。我们来看下面一个简单的代码：

int sumFunc(int n) {  int num = 0;     // 执行一次  for (int i = 1; i <= n; ++i) {  // 执行n次    num = num + i;         // 执行n次  }        return num;}

假设，每行代码的执行时间为t，那么这块代码的时间就是(2n+2)*t

由此得出：代码执行时间T(n)与代码的执行次数是成正比的！

那么我们来看下一个例子：

int sumFunc(int n) {  int num = 0;    // 执行一次  for (int i = 1; i <= n; ++i) {       // 执行n次    for (int j = 1; j <= n; ++j) {     //执行n*n次      num = num + i * j;         // 执行n*n次    }  }}

同理，该代码执行时间为(2n*n+n+1)*t，没意见吧？继续往后看！

注意： 在数据结构/算法中，通常使用T(n)表示代码执行时间，n表示数据规模大小，f(n)表示代码执行次数综合，所以上面这个例子可以表示为f(n)=(2n*n+n+1)*t，其实就是一个求总和的式子，O(大写O)表示代码执行时间与 f(n) 成正比例。

根据上面两个例子得出结论：代码的执行时间 T(n)与每行代码的执行次数 n 成正比，人们把这个规律总结成这么一个公式： T(n) = O(f(n))

所以呢，第一个例子中的 T(n)=O(2n+1)，第二个例子中的 T(n)=O(2n*n+n+1)，这就是时间复杂度表示法，也叫大O时间复杂度表示法。

但是，大O时间复杂度并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度，简称时间复杂度。

与泰勒公式相反的是，算了，扯哪去了…

当n变得越来越大时，公式中的低阶，常量，系数三部分影响不了其增长趋势，所以可以直接忽略他们，只记录一个最大的量级就可以了，所以上述两个例子实际他们的时间复杂度应该记为：T(n)=O(n) ，T(n)=O(n*n)

我想你应该明白大致是怎么回事了，那么我们来看看如何去计算它？

时间复杂度的分析与计算方法

（1）循环次数最多原则

我们上面说过了，当n变得越来越大时，公式中的低阶，常量，系数三部分影响不了其增长趋势，可以直接忽略他们，只记录一个最大的量级就可以了。因此我们在计算时间复杂度时，只需关注循环次数最多的那段代码即可。

int sumFunc(int n) {  int sum = 0;     //执行1次，忽略不计  for (int i = 0; i < n; i++) {    sum += i;    // 循环内执行次数最多，执行次数为n次，因此时间复杂度记为O(n)  }    return sum;    //执行1次，忽略不计}

（2）加法原则

int sumFunc(int n) {  int sum = 0;     //常量级，忽略    for (int i = 0; i < 99; i++) {    sum += i;  //执行100次，还是常量级，忽略  }
  for (int i = 0; i < n; i++) {    sum += i;  //执行n次  }
  for (int i = 0; i < n; i++){    for (int j = 0; j < n; j++) {      sum += i;  //执行n*n次    }  }  return sum;}

上述例子中，最大的两块代码时间复杂度分别为 O(n)和O(n*n)，其结果本应该是：T(n)=O(n)+O(n*n)，我们取其中最大的量级，因此整段代码的复杂度为：O(n * n)

所以得出结论：量级最大的那段代码时间复杂度=总的时间复杂度

（3）乘法原则

嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

void Func1(int n) {  for (int i = 0; i < n; i++) {    Func2(n);  //执行n次，每次都会调用Func2函数执行n次  }}void Func2(int n) {  int sum = 0;  for (int i = 0; i < n; i++)  {    sum += 1;  //执行n次  }}

因此这段代码时间复杂度为O(n) * O(n) = O(n*n) = O(n*n)

同理，如果将其中一个n换成m，那么它的时间复杂度就是O(n*m)

常见的几种时间复杂度

（1）O(1)常量级时间复杂度

void Func(void) {  for (int i = 0; i < 100; i++) {    printf("hello");  //执行一百次，也是常量级，记为O(1)  }}

void Func(void) {  printf("hello");  printf("hello");    printf("hello");    //各执行一次，还是记为O(1)}

相信你也看明白了，O(1)不是说代码只有一行，这个1它代表的是一个常量，即使它有以前一万行这样的也是O(1)，因为它是固定的不会变化（也就是常量）， 所以凡是常量级复杂度代码，均记为O(1)

（2）常见的O(n)复杂度

void Func(int n) {  for (int i = 0; i < n; i++) {    printf("hello");  }}

不用多说了吧！继续！

（3）O(logn)，O(nlogn) ，这就有点难度了！

首先我们来回忆以下换底公式：

记住公式啊，来看例子：

void Func(int n) {  for (int i = 1; i < n; i++) {    i = i * 2;  }}

可以看出，i = i * 2这行代码执行次数是最多的，那么到底执行了多少次呢？

第一次 i=2，执行第二次 i=4，执行第三次 i=8…

假设它执行了x次，那么x的取值为：

当上述代码的2改成3的时候，x的取值也就是：

当然不管log的底数是几，是e也好，是10也罢，统统记为：

这是为啥子念？由换底公式可以计算出：

换底之后，可以看出log3(2)其实就是一个常数，忽略它！而在这场游戏中，log默认就是以2为底的，所以统统记为O(logn)。

void Func(int n) {  for (int i = 0; i < n; i++) {    Func2(n);    //执行n次，嵌套调用，每次调用执行logn次  }}void Func2(int n) {  for (int i = 0; i < n; i++)  {    i = i * 2;    //执行logn次  }}