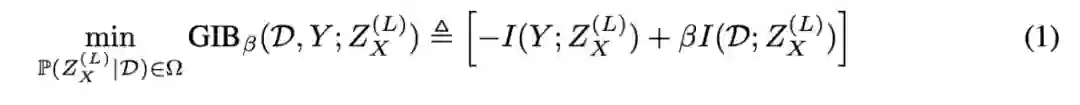什么是优秀的图表示？斯坦福提出首个信息论原则——图信息瓶颈

选自arXiv

作者 ： Tailin Wu  等

机器之心编译

编辑：魔王

对于图结构数据而言，什么是「优秀」的表示？斯坦福研究者对此进行了重新思考，并提出学习稳健图表示的信息论原则——图信息瓶颈 (GIB)。研究者基于该原则构建了两个 GNN 模型：GIB-Cat 和 GIB-Bern，二者在抵御对抗攻击时取得了优异的性能。

图表示学习旨在基于图结构数据学习表示，并用于节点分类、链路预测等下游任务。由于节点特征和图结构包含重要信息，因此图表示学习任务具备一定的挑战性。图神经网络（GNN）融合了来自节点特征和图结构的信息，因而具备优秀的性能。

近期，很多研究开始关注如何开发更强大的 GNN，使之拟合更复杂的图结构数据。然而，目前 GNN 仍然面临一些问题。例如，邻近节点的特征包括一些无用信息，可能对当前节点的预测产生负面影响。此外，GNN 依赖于通过图的边进行消息传递，这使它容易遭受针对图结构的噪声和对抗攻击。

近日，来自斯坦福大学的研究者希望解决以上问题，并重新思考：对于图结构数据而言，什么是「优秀」的表示？具体而言，信息瓶颈 (IB) 为表示学习提供了核心原则：最优表示应包含适合下游预测任务的最少充足信息。IB 鼓励表示最大程度地包含与目标相关的信息，以使预测结果尽可能准确（充足）。另一方面，IB 遏制表示从数据中获取与预测目标无关的额外信息（最少）。基于这一学习范式学得的模型自然而然可以避免过拟合，并对对抗攻击具备稳健性。

• 论文地址：https://arxiv.org/pdf/2010.12811.pdf

• 项目地址：http://snap.stanford.edu/gib/

• GitHub 地址：https://github.com/snap-stanford/gib

然而，将 IB 原则扩展到图表示学习的过程面临着以下两个独特的挑战：

• 首先，之前利用 IB 的模型假设数据集中的训练样本是独立同分布的 (i.i.d.)。对于图结构数据而言，该假设不成立，因此按照 IB 原则训练模型较为困难；

• 此外，结构信息对于表示图结构数据是必不可少的，但此类信息比较分散，因而很难进行优化。如何恰当地建模和从图结构中提取最少充足信息带来了另一项挑战。

解决办法：图信息瓶颈 (GIB)

该研究基于 IB 提出了一种信息论原则——图信息瓶颈 (Graph Information Bottleneck, GIB)，专门为图结构数据的表示学习打造。GIB 从图结构和节点特征中提取信息，并鼓励学得表示中的信息满足最少和充分两个原则（参见下图 1）。

为了克服非独立同分布数据带来的挑战，研究者利用图结构数据的局部依赖假设来定义最优 P(Z|D) 的搜索空间 Ω，其遵循马尔可夫链层级化地从特征和图结构中提取信息。研究者表示，这项研究为基于图结构数据的监督式表示学习提供了首个信息论原则。

图 2：GIB 原则利用局部依赖假设。

并得到：

研究者还为 GIB 扩展了变分上下界，使其更适合 GNN 的设计与优化。具体而言，该研究提出变分上界，用于约束从节点特征和图结构提取的信息；并用变分下界来最大化表示中的信息，以预测目标。

研究者将 GIB 原则应用于图注意力网络 (GAT)，利用 GAT 的注意力权重采样图结构，从而缓解优化和建模离散图结构的难度。研究者还分别基于类别分布和伯努利分布设计了两个采样算法，提出两个模型 GIB-Cat 和 GIB-Bern。GIB-Cat 和 GIB-Bern 算法参见 Algorithm 2 和 Algorithm 3，Algorithm 1 则展示了这两种算法的基础框架。

GIB-Cat 和 GIB-Bern 算法。

GIB-Cat 和 GIB-Bern 算法的基础框架。

实验表明，这两个模型可以提升标准基线模型的稳健性，性能超过其他 SOTA 防御模型。GIB-Cat 和 GIB-Bern 将对抗扰动情况下的分类准确率分别提升了 31.3% 和 34.0%。

实验

对抗攻击

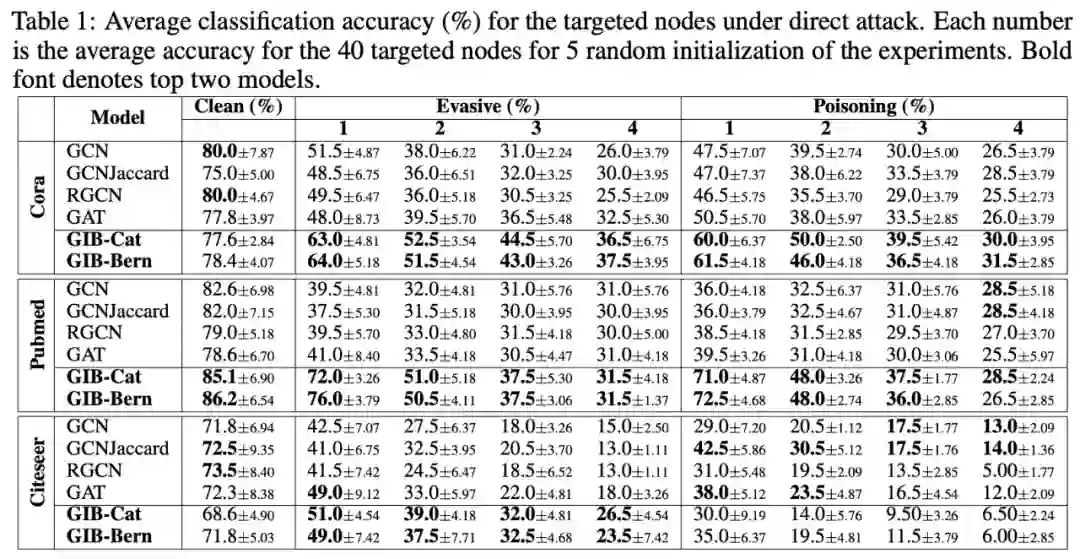
研究者对比了不同模型对对抗攻击的稳健性，实验结果参见下表 1。

从中可以看出，GIB-Cat 在 Cora 和 Pubmed 上的分类准确率相比 GAT 分别平均提高了 8.9% 和 14.4%，GIB-Bern 提高了 8.4% 和 14.6%，这表明 GIB 原则可以有效提升 GNN 的稳健性。值得注意的是，当扰动数值为 1 时，GIB-Cat 和 GIB-Bern 在 Pubmed 上的分类准确率相比 GAT 分别提升了 31.3% 和 34.0%。

特征攻击

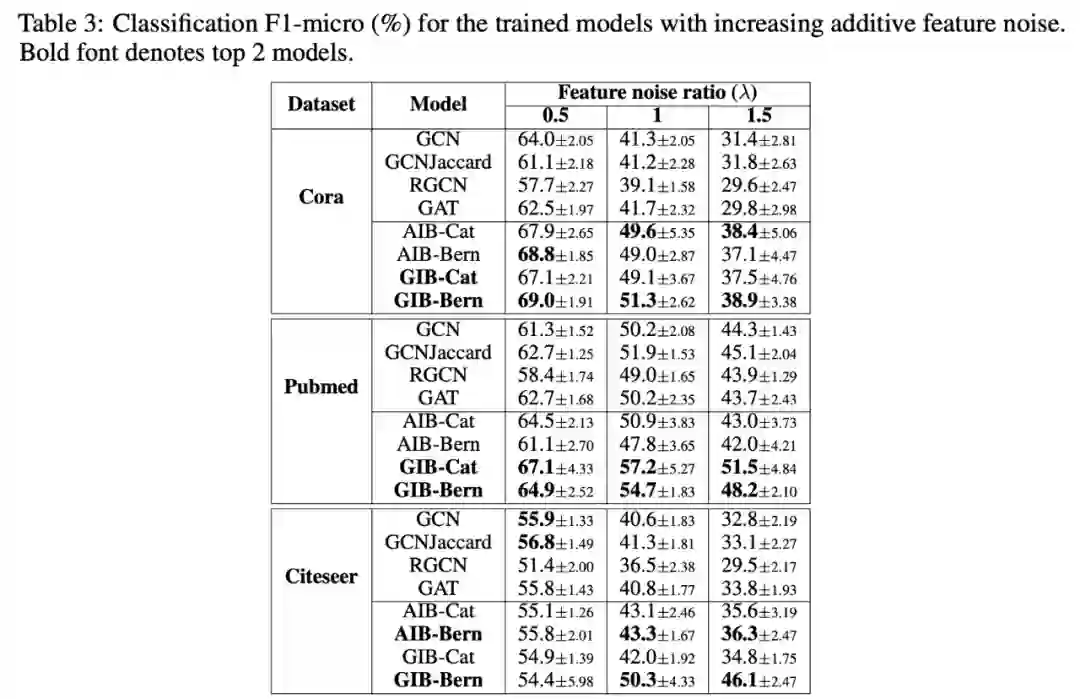
为了进一步确认 IB 对节点特征的有效性，研究者向节点特征引入随机扰动。实验结果参见下表 3：

从中可以看到，在不同特征噪声比率情况下，GIB-Cat 和 GIB-Bern 持续优于不使用 IB 的其他模型，尤其是当特征噪声比率较大 (λ = 1.5) 时，仅具备结构 IB 的 AIB 模型性能稍逊于或等同于 GIB 模型。这表明，当特征攻击成为扰动主要来源时，GIB 可使模型具备更强的稳健性。

Java工程师入门深度学习（二）：DJL推理架构详解

DJL是亚马逊推出的开源的深度学习开发包，它是在现有深度学习框架基础上使用原生Java概念构建的开发库。DJL目前提供了MXNet,、PyTorch和TensorFlow的实现。Java开发者可以立即开始将深度学习的SOTA成果集成到Java应用当中。

11月3日20:00 ，李政哲（AWS软件开发工程师）将带来线上分享，介绍DJL推理模块并结合具体场景讲解各模块使用方法，推理 API 的使用方法以及如何优化推理速度，如何部署在微服务、大数据服务以及移动端并搭配客户成功案例的讲解。

• 添加机器之心小助手：syncedai5，邀请加入DJL交流群。

• 点击阅读原文，注册直播。

© THE END 

转载请联系本公众号获得授权

投稿或寻求报道：content@jiqizhixin.com