中科院计算所最新《时态数据因果发现》综述，50页pdf详述多元时间和事件序列因果发现

**时态数据是一种典型的数据结构，用于描述复杂系统的时间序列，在工业、医学、金融等领域有着广泛的应用。**分析这种类型的数据对各种应用都非常有价值。因此，在过去的几十年里，不同的时态数据分析任务，如分类、聚类和预测，被提出。其中，因果发现，即从时序数据中学习因果关系，是一项有趣而关键的任务，受到了广泛的研究关注。根据时序数据是否经过校准，现有的因果关系发现工作可以分为两类，即多元时间序列因果关系发现和事件序列因果关系发现。然而，以往的研究大多只关注时间序列的偶然发现，而忽略了第二类偶然发现。本文详细说明了这两类之间的相关性，并对现有的解决方案进行了系统的概述。提供了时态数据因果发现的公开数据集、评估指标和新视角。

1. 引言

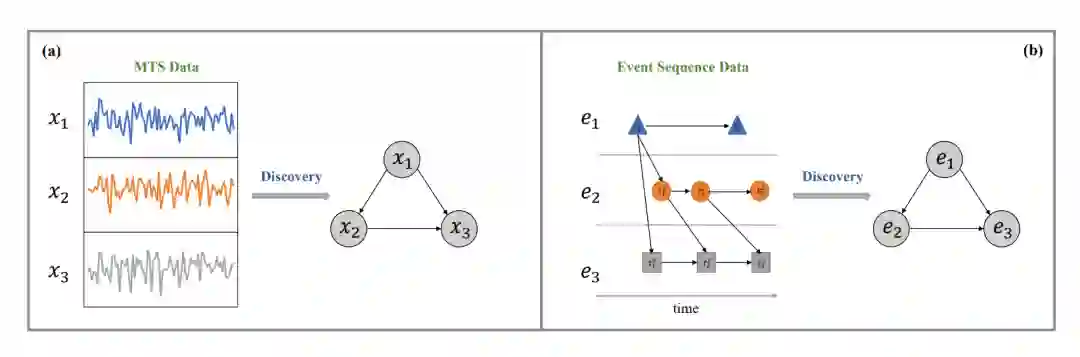
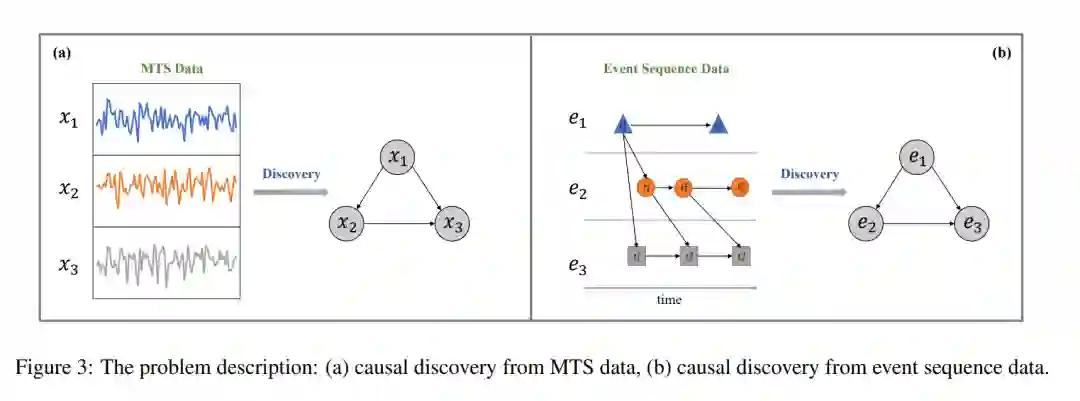
社会网络、生物信息学、神经科学、金融等领域广泛收集记录复杂系统状态变化的时态数据。时态数据是最常用的数据结构之一，由按时间排序的属性序列组成。近年来，随着传感器和计算设备的快速发展，时态数据分析的研究工作不断涌现。人们针对不同的任务提出了不同的方法，如分类[1,2]，聚类[3,4]，预测[5]，因果发现[6,7]等。其中，因果发现识别众多时态成分之间的因果关系已成为时态数据分析中一项具有挑战性但至关重要的任务。学习到的因果结构有助于解释数据的生成过程，指导数据分析方法的设计。根据数据是否经过校准，用于因果发现的时间数据可以分为两类，即多元时间序列(MTS)和事件序列。因此，现有的因果发现方法也可以分别分为两类。本综述旨在提供一个深思熟虑的概述，并总结时序数据因果发现的前沿。 MTS数据描述了多个变量随时间变化的标定状态，在许多领域是一种通用的时态数据。发现MTS的因果关系有助于提高数据分析模型的可解释性和鲁棒性。然而，因果关系的定义并不唯一，导致了不同的解决方案。现有的研究工作可以分为四类，即基于约束的方法、基于评分的方法、基于功能因果模型(functional causal model, FCM)的方法和Granger因果方法。此外，也存在一些新的视角，如Takens的因果关系和微分方程。本文将详细说明每个类别的主要思想和最新进展。事件序列中的因果关系发现是事件序列中的另一项任务，它在非规则和异步观察到的时间序列中推断因果关系。具体来说，它将不同事件的序列作为输入，并输出表示不同事件之间因果相互作用的因果图。这项任务非常重要，因为现实世界中的大多数事件不能在固定的时间间隔内出现。根据MTS任务，将相应的方法分为三大类:基于约束的方法、基于得分的方法和基于Granger因果关系的方法。在这三类方法中，基于Granger因果关系的方法，特别是基于Granger因果的霍克斯过程模型，由于Granger因果关系和霍克斯过程之间存在天然的匹配，得到了较好的发展。我们将在本综述中进一步详细描述这些方法。

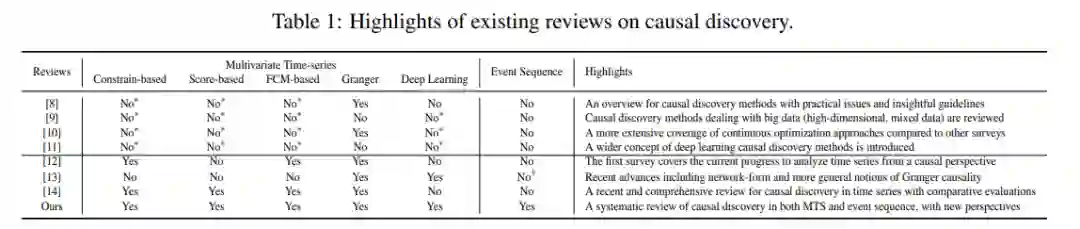
最近，许多研究[8,9,10,11,12,13,14,15,16,17]被发表来总结偶然发现的进展。我们比较了表1中具有代表性的评论及其亮点。如图所示，这些调研分为两行。第一行[8,10,9,11]的研究工作从不同的角度讨论了一般的因果发现问题。例如，[8]给出了计算因果关系发现方法的简要综述。[10]专注于持续优化方法的快速发展。为了处理大数据，在[9]中引入了基于机器学习的因果推理和因果发现方法。此外，回顾了不同变量范式下的深度学习因果发现方法，从更广阔的视角讨论了数据中的因果关系。这些论文将时态数据作为一种特殊的应用，并没有包括许多数据指定的方法。第二行中的调查侧重于时态数据的偶然发现。如表1所示，[6,7]综述了二元时间序列的因果发现方法。最近，[12,13]对时间序列中的因果推理方法进行了综述。最近的工作[14]对已有的时间序列因果发现方法进行了讨论和比较评估。然而，这些综述忽略了事件序列的因果关系发现方法。文中不仅对这两种时态数据的因果关系发现方法进行了全面的综述，而且分析了它们之间的联系和区别。

其次，在第2节中，我们首先介绍了偶然发现问题的背景和初步研究。第3节和第4节分别介绍了MTS和事件序列因果关系发现的最新进展。然后，在第5节中概述了时态数据因果发现的应用，在第6节中总结了可用的资源。最后，在第7节中讨论了现有时态数据因果关系发现方法的局限性和新发展方向。

2. 多元时间序列的因果发现

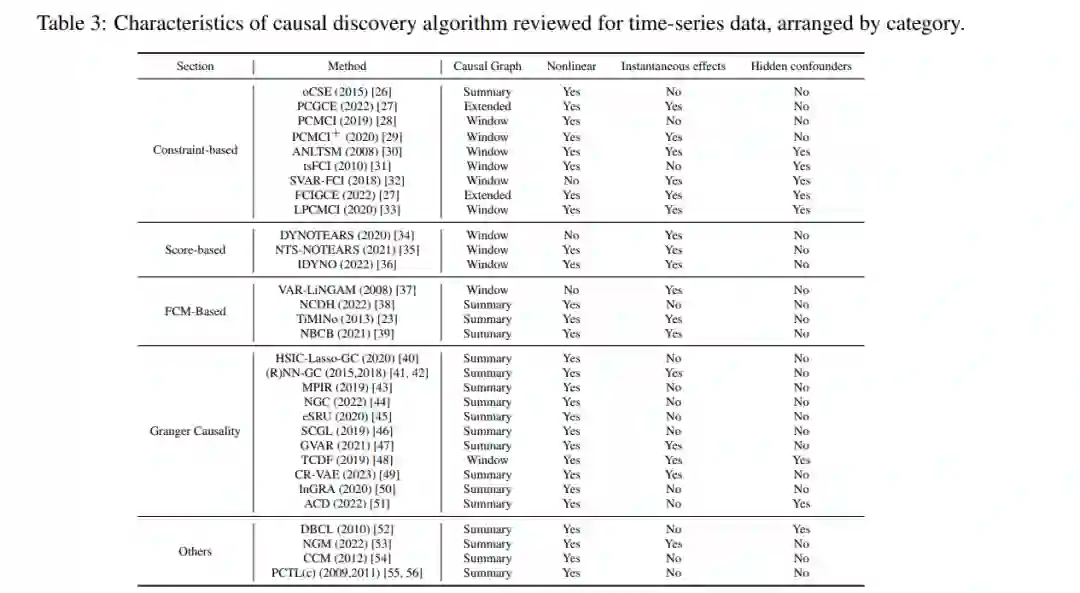
在本节中，我们回顾了多变量时间序列数据的因果发现方法，包括基于约束的方法、基于评分的方法、基于功能因果模型的方法、Granger因果关系等。结合这些特点，具有代表性的算法总结在表3中。

3.1 基于约束的方法

作为一类因果关系发现算法，基于约束的方法依赖于条件独立性的统计检验，易于理解且应用广泛。首先给出了基于约束的方法的主要思想，包括一般步骤和因果假设。详细的方法将分为有因果充分性假设和无因果充分性假设两类，并分别介绍。一般步骤是:首先，基于条件独立性建立变量间的骨架;其次，根据规则中的方向准则对骨架进行方向估计;目标是构建表示真实因果图的MEC的完全部分有向无环图(CPDAGs)。这些从观察中得出MEC的方法的核心是因果假设。这些方法通常是在因果马尔可夫性质和忠实度的假设下进行的，有些还假设因果充分性(没有未观察到的混杂因素)。在本节中，我们首先回顾了因果充分性假设下的主要算法及其对时序数据的扩展，然后介绍了当因果充分性假设不确定时的处理方法。

3.2 基于分数的方法

另一类因果发现方法是基于得分函数的。首先介绍基于评分的方法的主要思想，包括(动态)贝叶斯网络、基于评分的方法与基于约束的方法相比的特点、模型评分和模型搜索。然后，分别回顾MTS的组合搜索方法和连续优化方法; 3.3 FCM-Based方法

上述两类方法要么面临MEC的不可分离性，要么需要大样本来确认因果忠实度。因果发现也可以基于功能因果模型(Functional Causal Models, FCM)进行[89]，也称为2.1中的SCM，通过一组方程来描述因果系统。近年来，基于FCM的时间和非时间数据处理方法大量涌现。在本小节中，我们首先介绍基于FCM方法的主要思想，包括功能因果模型和噪声在因果关系定位中的使用。然后分别介绍两类基于FCM的方法，即基于独立分量分析的方法和基于加性噪声模型的方法。在FCM中，每个变量都用一个方程来解释其直接原因和一些额外的噪声。例如，函数xj = fj (xi, uj)解释了xi→xj与一些额外的噪声uj的因果关系。基于FCM的因果发现方法的一个基本思想是，统计噪声可以是一个有价值的见解来源，这迎合了最近的发现[90]，挑战了噪声应该被视为讨厌的正统观点。其中，因果关系可以借助噪声进行识别和估计。

3.4 基于Granger因果关系的方法

Granger因果关系是分析时间序列数据的常用工具。有许多因果发现方法都是在Granger因果关系的基础上发展起来的。在这一小节中，我们首先介绍Granger因果关系的定义。在深入研究具体方法之前，将给出两类MTS Granger因果关系模型(无模型和基于模型)并进行比较。由于基于模型的方法在更一般的情况下具有优越性，本文的其余部分将重点介绍基于模型的方法的两个最新进展:(1)基于核的方法(3.4.3)，以及(2)基于神经网络的方法(3.4.4)。

3.5 其他

上述四类方法已经成为因果发现研究的主题。为了保证方法的完备性，本节将介绍5种不同于上述方法的方法，包括基于信息论统计的因果关系方法、基于微分方程的因果模型方法、非线性状态空间方法、基于逻辑的方法和混合方法。 4 事件序列的因果关系发现

多元时间序列的一个重要假设是时间戳是离散的，时间间隔是固定的。然而，在现实世界中，绝大多数事件不会以固定的时间间隔发生。因此，我们需要想出一些方法来处理这些不规则和异步的数据。我们可以将事件序列构建为{(t1, e1)，(t2, e2)，…}，其中第一个维度表示对应事件发生的时间，第二个维度表示对应的事件类型。在本节中，我们将专注于推断事件序列中的因果关系。首先，介绍了多元点过程，为事件序列的因果发现做了初步的介绍;然后，我们回顾了基于格兰杰因果模型的方法，这些方法是很好的发展。最后，给出了基于约束的方法和基于分数的方法。 5. 应用

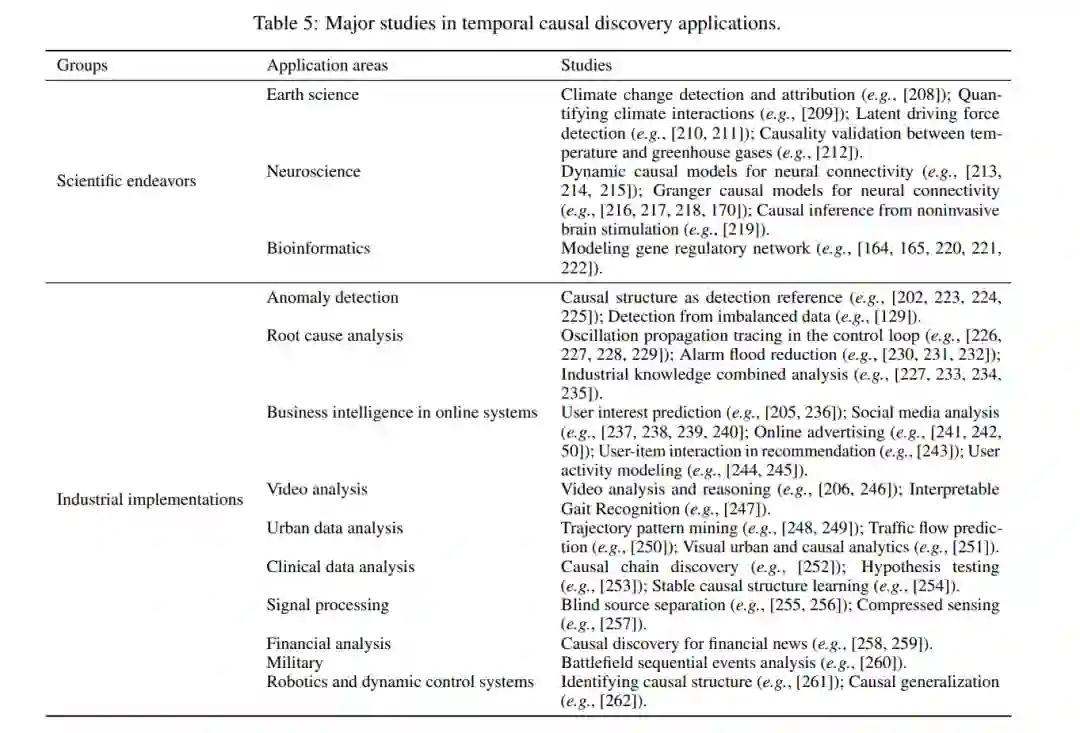
时序因果发现已被广泛应用于许多领域，如科学努力(地球科学[197]，神经科学[198,199,200]，生物信息学[201])，工业实现(异常检测[202]，根本原因分析[203,204]，在线系统中的商业智能[205]，视频分析[206])。表5总结了该方法的应用领域和相关研究。对于科学研究而言，学习到的因果关系通常不应被视为最终结果，而应被视为进一步研究的起点和假设[207]。作为一种推动者，因果发现可以在工业环境中的多阶段方法中发挥支持作用[203]。在本节的其余部分中，我们将回顾三个领域，包括地球科学、异常检测和根本原因，以解释将时间因果发现分别纳入科学努力和工业实施的主要工作流程。