《四元数神经网络进展》最新138页

本论文研究了四元数神经网络（QNN）的构建、优化以及在美国国防部（DoD）相关问题集中的应用。QNN 是一种神经网络，其权重、偏置和输入值均以四元数表示。长期以来，四元数一直被用于信号处理和机器人应用中，越来越多的研究表明，四元数神经网络在基本任务和高维问题集方面的表现优于实值神经网络。然而，这种性能提高的许多原因仍有待探索，研究 QNN 优化动态的文献仍存在很大差距。本论文填补了其中的几个空白。这项工作对文献中存在的无数不同的四元数反向传播推导进行了批判性评估，并在一系列回归问题集上测试了每种推导的性能。论文探讨了 QNN 的优化动态，展示了 QNN 损失面的可视化，以及评估这些损失面 “平滑度 ”的新方法。最后，本论文介绍了深度强化学习（DRL）算法中 QNN 与四元深度 Q 网络（QDQN）算法的新型集成。QDQN 代表了迄今为止 QNN 研究的顶峰，为进一步的研究和探索奠定了基础，在先进的自主系统 (AS) 和机器人控制应用中，在充分利用四元数代数结构的问题集中利用 QNN。

美国国防部（DoD）和整个美国政府越来越认识到人工智能/机器学习（AI/ML）和自主应用的潜在影响。这种日益增长的关注是由这些技术对国防行动、美国劳动力所具有的变革潜力以及在作战中使用此类系统的道德和伦理影响所驱动的。2018 年国防部人工智能战略》指出："人工智能正在迅速改变各种业务和行业。它还准备改变未来战场的特征和必须面对的威胁的速度"。近年来，这种转变的速度不断加快，推动着人工智能/ML 研究成为国防部战略发展和投资的最前沿。本论文研究了四元数神经网络（QNN）的构建和使用，将其作为一种关键的使能技术，促进稳健、可靠的机器学习方法和自主系统（AS）的发展。

四元数是复数的四维扩展，包含几个重要的代数特性。复数在信号处理和电子工程应用中无处不在，因为它能简洁地表示复平面中的二维矢量旋转，而四元数同样能简洁地表示三维空间中的矢量旋转。图 1 举例说明了当三维空间中的矢量用纯四元数表示时，三维矢量旋转如何简化为两个四元数乘法运算。

本论文的结构如下： 第二章简要回顾了四元数代数并介绍了四元数神经网络。第三章至第五章介绍了论文的三个主要研究内容。最后，第六章提出了总体结论和未来工作建议。

第三章的重点是对四元神经网络文献进行全面而严谨的分析，因为它与四元域中的神经网络反向传播算法相对应。在进行反向传播训练 QNN 时，四元数需要考虑一些特殊因素，文献中存在无数关于四元反向传播的推导。这项工作提供了一个精心构建的实验，以检验每种不同反向传播方法的性能。实验结果根据各种指标进行评估，并进行了重复，以确保统计的严谨性。通过这些重复实验，可以进行稳健的统计测试，以确定各种指标（包括网络准确性和计算效率的多种衡量标准）中性能最佳的算法。

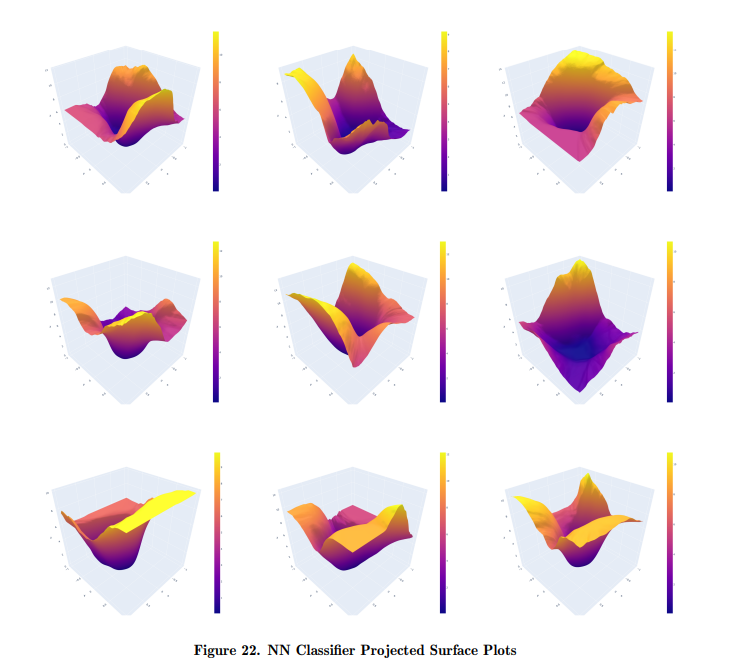
第四章研究 QNN 的优化动态。这项研究利用实值神经网络文献中的损失面可视化和投影技术，首次探索了基于四元数的优化损失面。研究介绍了利用曲面曲率估计值对损失曲面 “好坏 ”进行稳健定量测量的方法。本章还进行了广泛的计算测试，以证明曲面曲率估计值的有效性。最后，本章介绍了经过调整的 QNN 模型与经过调整的实值 NN 模型在回归任务和分类任务中的平均表面曲率的稳健统计比较。实验证明，QNN 模型的损失曲面在统计上明显比实值模型更平滑，这为 QNN 在各种问题领域的优化性能提升提供了强有力的支持。

第五章是本论文主要研究的顶点。本章介绍了将 QNN 整合到深度强化学习（DRL）算法中的新方法，即四元数深度 Q 网络（QDQN）算法。在 OpenAI Gym 测试环境套件中的两个标准 DRL 基准任务上，检验了 QDQN 与实值深度 Q-Network (DQN) 算法的性能对比。实验设计参数和随机数种子都经过严格控制，因此结果具有可重复性和可辩护性。在这些测试环境中，QDQN 与 DQN 的对比评估证明了 QDQN 在具有挑战性的 DRL 任务中的有效性和可行性。

最后，第六章对论文进行了总结。论文给出了总体结论，并为今后的工作提供了几条可行的途径。