《无人机群优化》洛克希德马丁14页报告（2022）

由于无人驾驶系统（包括无人机、自动驾驶汽车、仓库机器人等）的增长和前景，多Agent路径寻找（MAPF）是一项重要性迅速扩大的挑战，也是一项受益于新型计算技术的挑战。

本案例研究的工作是在有限的时间窗口内测试不同的技术来解决MAPF问题。主要结论是MemComputing公司开发的虚拟记忆计算机（VMM）在竞争中优于专门为MAPF问题类开发的基于A*的CBS搜索算法，以及更多的整数线性规划问题的通用求解器，如CPLEX。正如预期的那样，CPLEX的表现比CBS差，因为CBS是一种解决MAPF问题的专门方法。这些结果表明，VMM，也就是MemComputing，很适合有效地解决MAPF这样的组合优化问题。

随着问题规模的扩大，VMM的加速度也在增加。VMM是唯一能找到所有20个Agent方案和大部分30个Agent方案的解决方案的求解器，也是唯一能找到40个Agent方案的求解器。作为一个通用的ILP求解器，VMM更加灵活，能够扩大MAPF问题的范围。使用更长的运行时间（超过10分钟）将使VMM能够继续改进其结果。

一句话。这些发现支持将MemComputing概念，包括VMM，应用于多Agent人工智能优化应用的优势。

进一步思考：虽然没有包括在这个案例研究中，但MemComputing解决方案可以进一步加速。例如，我们已经探索了MAPF问题的非线性类型的实现，我们估计可以在VMM上提供超过100倍的加速。最终，MAPF问题最好在VMM上运行，在FPGA上实现，或者最好是基于MemComputing的特定应用集成电路（ASIC）。在幕后，VMM是对电子电路的模拟，因此，将VMM一直发展到专门的ASIC是我们的产品路线图。一个MemComputing ASIC将为几乎不确定规模的MAPF问题提供一个接近实时的解决方案。

引言

由于技术的进步和创新应用，人工智能（AI）正在迅速发展。从虚拟助手到自动驾驶汽车，人工智能正在被部署到几乎每一个行业。然而，在开发先进的人工智能方面仍然存在着巨大的计算挑战。

一个被充分研究的问题被称为多Agent路径寻找（MAPF）问题[1]。MAPF问题支持仓库自动化、交通优化、包裹运送、机器人和自主车辆的应用。Agent通常指的是移动自主系统，如无人机、机器人或其他自主车辆。这个问题的目标是寻找路径，使许多Agent能够安全有效地从各自的起始位置同时导航到各自的目的地。此外，这些Agent必须不阻挡、不碰撞或以其他方式相互干扰，而且它们的路径必须是最优的，这使得这个问题在计算上具有挑战性。以最优或接近最优的方式解决这个问题有巨大的好处，因为它将提高运行效率和节省大量成本，从而推动战略竞争优势。

像亚马逊和阿里巴巴这样的全球电子商务巨头在他们的自动化仓库中每天都面临着MAPF问题，机器人在其中发挥了关键作用。机器人每周7天每天24小时运行，自动执行客户履约任务，如在他们的大型仓库中拣选、运输和放置货物，这些仓库有许多城市街区大小。

案例研究

在这个案例研究中，我们展示了我们基于云的虚拟计算机（VMM）是如何为洛克希德-马丁公司解决一个复杂的MAPF问题的，该公司是世界上最大的航空航天和国防承包商之一。该用例的灵感来自于假设Agent是一群无人机，每架无人机都有自己的特定任务。然而，无论Agent的类型或目的如何，该问题都广泛适用。

由于这个问题的难解性[2]，目前的方法，甚至是亚马逊和阿里巴巴使用的方法，都依赖于只能提供近似解决方案的启发式方法。然而，近似值会导致Agent必须采取回避行动来避免彼此，或者在某些情况下会一直陷入僵局的情况。这肯定会导致灾难的发生。在这里，我们将展示如何使用我们的VMM在战术上相关的时间范围内解决这个问题和类似的问题。

对于这个案例研究，我们解决多Agent路径寻找（MAPF）问题[1]，并考虑到Agent可以是无人机群。从空中侦察到破坏敌方通信，甚至与敌方部队交战，战斗管理者非常需要开发先进的无人机群技术。无人机的协调规划和规模分配可以带来显著的作战优势，并大大增强作战人员的能力。

问题概述

让我们回顾一下MAPF问题的基本原理，以及为什么它如此难以解决。同样，目标是为环境中的多个Agent找到飞行计划，而不互相干扰，同时为每个无人机提供最佳路径。

行进的地图由一个图来描述。例如，一个二维地图可以被编码为一个二维网格，其边缘连接最近的邻居，沿心线有四个连接，如果包括对角线路径，则有八个连接。每条边都可能有一个相关的穿越成本。通常情况下，这个成本是旅行时间，但也可以是为任务定义的其他成本。

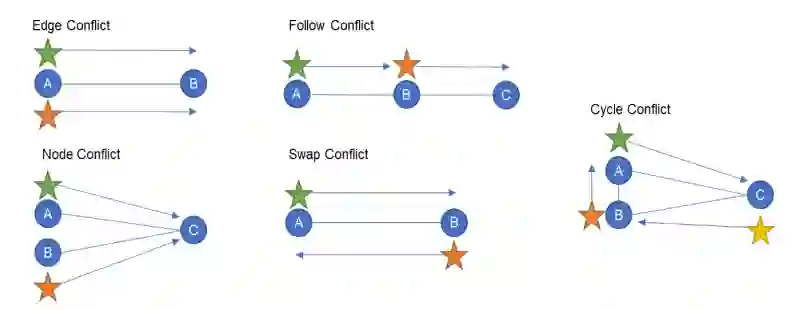
为了给一组Agent找到一个可行的解决方案，我们必须考虑在规划期间可能出现的冲突。如果任何两个单一代理人的计划之间没有冲突，那么MAPF解决方案被认为是有效的。在本案例研究中，我们考虑了一些潜在的冲突：

边缘冲突，即Agent在同一时间段内穿越同一边缘。
节点冲突，即Agent在同一时间段内到达同一节点。
交换冲突，即两个Agent试图占据对方的先前位置。

额外的冲突可以很容易地被添加到模型中，例如：

跟随冲突，即Agent占据以前占据的节点。
循环冲突，其中多个Agent试图交换先前的位置。

多Agent寻路是一个组合优化问题。也就是说，当Agent数量线性增加时，避免碰撞的复杂性可以比多项式地增长[2,3]。下一节将描述MAPF问题的一个简单示例。

为了让大家了解这个问题的难度，让我们考虑在一张小地图上只有两个Agent。必须为Agent1和Agent2找到最佳路径，以便从他们的起始位置移动到他们的目的地。他们每个Agent都有许多可能的路线来到达目的地。因为两者必须避免相互冲突，一个Agent的路线选择取决于另一个Agent的路线选择，此外，不能假设Agent在地图上以最短路径线性移动。