几何图神经网络综述：数据结构、模型与应用

几何图是一种具有几何特征的特殊图形，对于建模许多科学问题至关重要。与通用图不同，几何图通常展现出物理对称性，如平移、旋转和反射，使得现有的图神经网络（GNNs）处理它们时效率不高。为了解决这个问题，研究人员提出了多种具有不变性/等变性属性的几何图神经网络，以更好地表征几何图的几何性和拓扑结构。鉴于该领域当前的进展，进行一项关于几何GNNs的数据结构、模型和应用的全面综述是必要的。在本文中，基于必要但简洁的数学预备知识，我们提供了一个从几何消息传递角度对现有模型的统一视角。此外，我们总结了应用及相关数据集，以便于后续研究方法开发和实验评估的研究。我们还在这篇综述的最后讨论了几何GNNs的挑战和未来潜在发展方向。

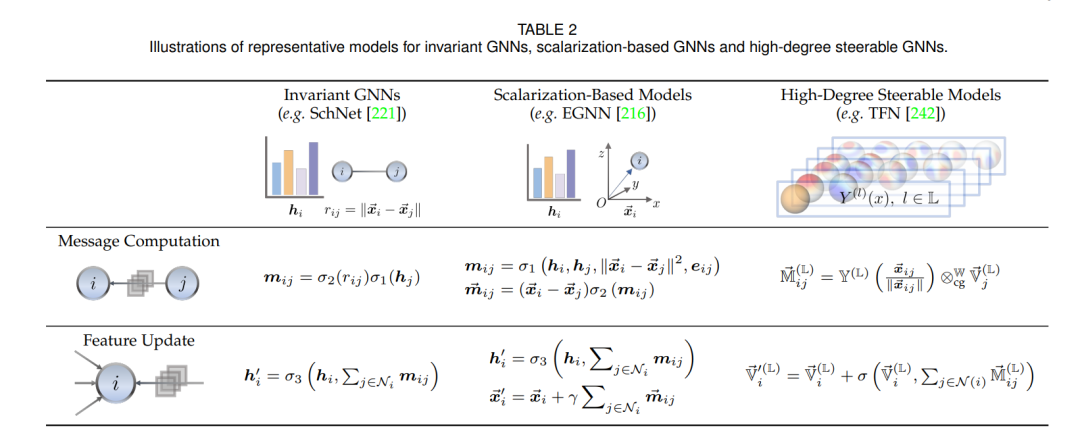
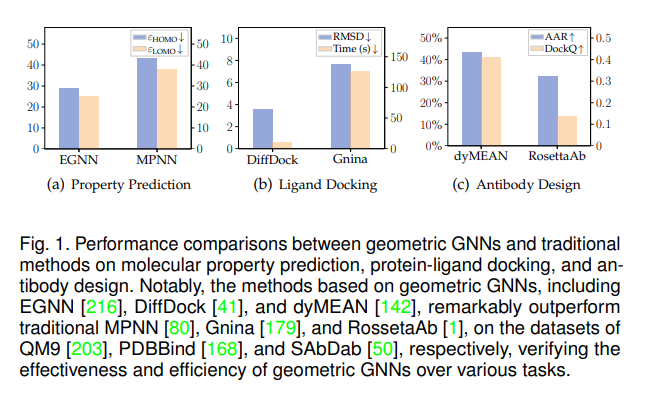
许多科学问题，特别是在物理和生物化学领域，需要处理以几何图形式表示的数据【24】。与典型的图数据不同，几何图还为每个节点分配一种特殊类型的节点特征，以几何向量的形式存在。例如，一个分子/蛋白质可以被视为一个几何图，其中原子的三维位置坐标是几何向量；在一般的多体物理系统中，粒子的三维状态（位置、速度或自旋）是几何向量。值得注意的是，几何图展现出平移、旋转和/或反射的对称性。这是因为控制原子（或粒子）动力学的物理定律无论我们如何将物理系统从一个地方平移或旋转到另一个地方都是相同的。处理这类数据时，将对称性的归纳偏见纳入模型设计至关重要，这激发了几何图神经网络（GNNs）研究的动机。 构建允许此类对称性约束的GNNs一直是方法设计的挑战。先驱方法如DTNN【222】、DimeNet【135】和GemNet【136】，将输入的几何图转换为与旋转或平移不变的距离/角度/二面角基标量，构成不变GNNs家族。注意到不变GNNs表达能力的限制，EGNN【216】和PaiNN【219】在消息传递和节点更新中额外涉及几何向量，以保留每层中的方向信息，从而导致等变GNNs。借助群表示理论作为有用的工具，TFN【242】、SE(3)-Transformer【67】和SEGNN【23】通过将它们视为由高阶球面张量参数化的可导向向量，概括了不变标量和等变向量，产生了高度可导向的GNNs。在这些基本方法的基础上，几何GNNs在各种系统的多样化应用中取得了显著成功，包括物理动力学模拟【67, 216】、分子性质预测【15, 152】、蛋白质结构预测【9】、蛋白质生成【267, 110】和RNA结构排名【245】。图1展示了几何GNNs在代表性任务上相对于传统方法的卓越性能。

为了促进几何GNNs的研究，本工作提出了一个系统性的综述，既关注方法也关注应用，其结构如下各节所示：在§ 2中，我们介绍了群论的必要初步知识和等变性/不变性的正式定义；在§ 3中，我们提出几何图作为一个通用的数据结构，将在整个综述中作为真实世界数据与模型（即几何GNNs）之间的桥梁；在§ 4中，我们将现有模型总结为不变GNNs（§ 4.2）和等变GNNs（§ 4.3），而后者进一步分类为基于标量化的模型（§ 4.3.1）和高度可导向的模型（§ 4.3.2）；此外，我们还在§ 4.4中介绍了几何图变换器；在§ 5中，我们提供了一个全面的应用集合，这些应用证明了几何GNNs在基于粒子的物理系统、分子、蛋白质、复合物以及像晶体和RNA等其他领域的成功。

本综述的目标是通过数据结构、模型设计和应用提供一个全面概览，构成一个完整的输入输出流程，对于希望在各种科学任务上使用几何GNNs的机器学习实践者具有指导意义。最近，已经提出了几个相关的综述，这些综述主要关注几何GNNs的方法论[52]、用于化学数据的预训练GNNs[276]、分子的表示学习[89, 7]，以及人工智能在不同类型科学系统中的通用应用[299]。与它们所有的不同之处在于，本综述强调几何图神经网络，不仅包含了几何GNNs的理论基础，还提供了一个涵盖物理、生物化学和材料科学等领域相关应用的详尽总结。同时，我们在§ 6中讨论了未来的前景和有趣的研究方向。我们还发布了一个Github仓库，收集了与几何GNNs相关的参考资料、数据集、代码、基准和其他资源。

几何图

在许多应用中，我们处理的图不仅包含拓扑连接和节点特征，还包含一定的几何信息。再次以分子为例，我们可能还会了解到欧几里得空间中的一些几何量度，例如，原子在3D坐标中的位置[4]。这些量度特别引人关注，因为它们封装了丰富的方向信息，描绘了系统的几何结构。有了几何信息，我们可以超越对图拓扑的有限感知，而是转向整个系统在3D空间中配置的更广阔图景，其中重要信息，如邻近节点的相对方向和方向量度（如速度），可以被更好地利用。因此，在本节中，我们从几何图的定义开始，这些通常被称为3D图[24]。 几何图是强大且通用的工具，用于在科学任务中建模各种对象，包括小分子[221, 216]、蛋白质[10, 110]、晶体[175, 118]、物理点云[102, 91]等等。我们将在§ 5中提供更多细节。

模型：几何GNNs

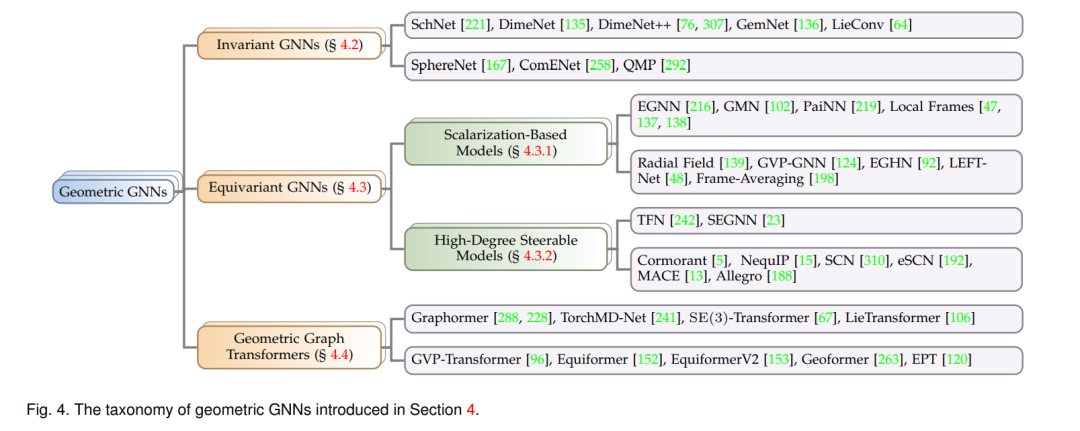
在本节中，我们首先回顾了拓扑图上消息传递神经网络（MPNN）的一般形式。然后，我们介绍了能够处理几何图的不同类型的几何GNNs：不变GNNs、等变GNNs，以及几何图变换器。最后，我们简要介绍了讨论几何GNNs表达能力的工作。图4展示了本节中几何GNNs的分类。

应用

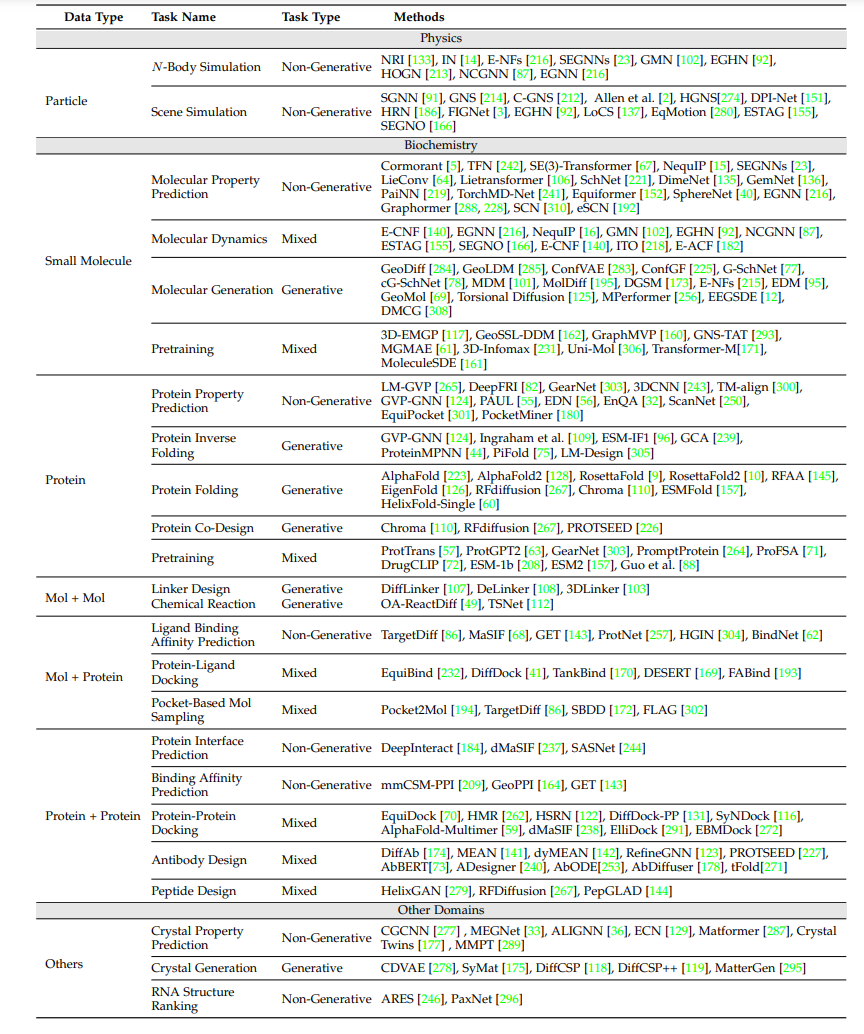
在本节中，我们系统地回顾了与几何图学习相关的应用。我们根据所处理的系统类型对现有方法进行分类，从而将任务分为粒子、（小）分子、蛋白质、分子+分子（Mol+Mol）、分子+蛋白质（Mol+Protein）、蛋白质+蛋白质以及其他领域，如表3所总结的那样。我们还分别在表4和表5中提供了单实例任务和多实例任务相关数据集的总结。值得一提的是，我们的讨论主要集中在使用几何GNNs的方法上，尽管在某些应用中，其他方法，如基于序列的方法，也可能适用。

结论

在这篇综述中，我们系统地研究了几何图神经网络（GNNs）的进展，通过数据结构、模型及其应用的视角。我们将几何图指定为数据结构，这在几何信息存在的情况下推广了图的概念，并允许在某些转换下保持关键的对称性。我们将几何GNNs作为模型来介绍，包括不变GNNs、基于标量化/高度可导向的等变GNNs，以及几何图变换器。我们通过数据和任务的分类，详尽讨论了它们的应用，包括物理、生物化学等领域的单实例和多实例任务，以及像材料和RNA这样的其他领域。我们还讨论了几何GNNs的挑战和未来潜在的发展方向。