深度学习在数学推理中的应用综述

数学推理是人类智能的一个基本方面，可应用于科学、工程、金融和日常生活等各个领域。能够解决数学问题和证明定理的人工智能系统的发展引起了机器学习和自然语言处理领域的重大兴趣。例如，数学是对强大的深度学习模型具有挑战性的推理方面的测试平台，推动新的算法和建模的进步。另一方面，大规模神经语言模型的最新进展为使用深度学习进行数学推理开辟了新的基准和机会。本文回顾了过去十年数学推理和深度学习交叉点的关键任务、数据集和方法。对现有的基准和方法进行了评估，并讨论了该领域未来的研究方向。

1. 引言

数学推理是人类智能的一个关键方面，它使我们能够根据数字数据和语言来理解和做出决定。它适用于科学、工程、金融和日常生活等各个领域，涵盖了从模式识别和数值运算等基本技能到解决问题、逻辑推理和抽象思维等高级技能的一系列能力。能够解决数学问题和证明定理的人工智能(AI)系统的发展一直是机器学习和自然语言处理(NLP)领域的一个长期研究重点，可以追溯到20世纪60年代(Feigenbaum et al.， 1963;Bobrow, 1964)。近年来，人们对这一领域的兴趣激增，如图1所示。

深度学习在各种自然语言处理任务中表现出巨大的成功，如问答和机器翻译(Sutskever等人，2014;Devlin等人，2018)。类似地，研究人员开发了各种用于数学推理的神经网络方法，已被证明在解决数学应用题解决、定理证明和几何问题解决等复杂任务方面是有效的。例如，基于深度学习的数学应用题解决者采用了一种带有注意力机制的序列到序列框架来生成数学表达式作为中间步骤(Wang et al.， 2018a;Chiang and Chen, 2019)。此外，通过大规模语料库和Transformer模型(Vaswani et al.， 2017)，预训练语言模型在各种数学任务上取得了有希望的结果。最近，像GPT-3 (Brown et al.， 2020)这样的大型语言模型(LLM)在复杂推理和上下文学习方面表现出了令人印象深刻的能力，进一步推进了数学推理领域。

最近在数学推理研究方面的进展令人印象深刻和鼓舞人心。本文综述了深度学习在数学推理中的进展。本文讨论了各种任务和数据集(第2节)，并研究了神经网络(第3节)和预训练语言模型(第4节)在数学领域的进展。本文还探索了基于大型语言模型的上下文学习的快速进展(第5节)，用于数学推理。进一步分析了现有的基准，发现对多模态和低资源设置的关注较少(第6.1节)。循证研究表明，当前的数值表示是不够的，深度学习方法对于数学推理不一致(第6.2节)。从泛化和鲁棒性、可信推理、从反馈中学习和多模态数学推理等方面改进当前的工作是有益的(第7节)。

2 任务和数据集

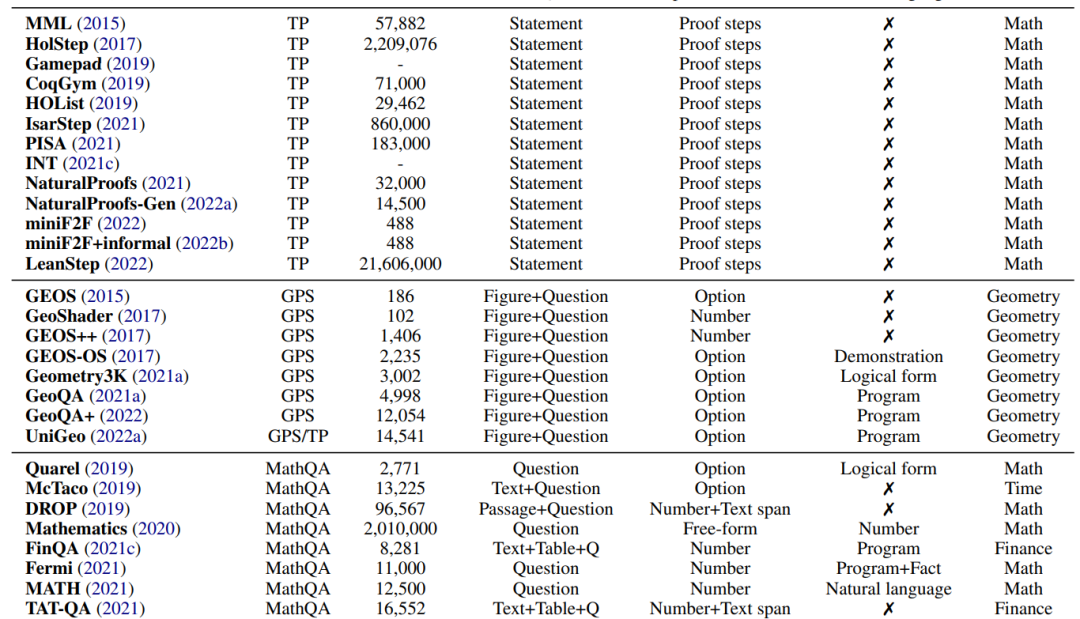
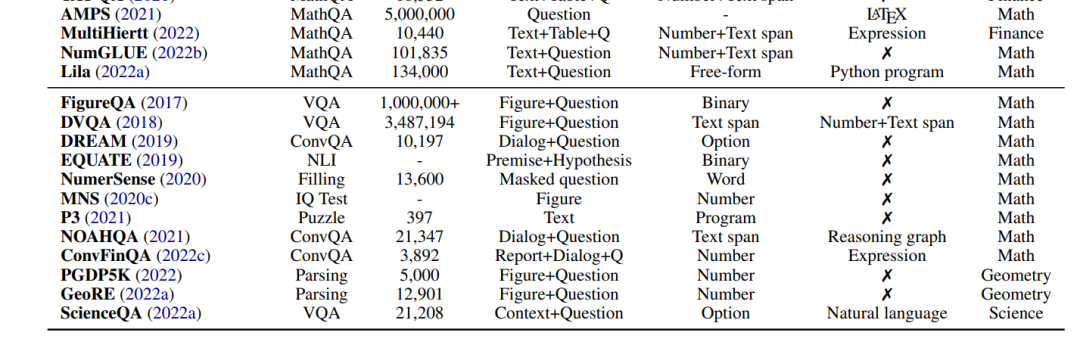
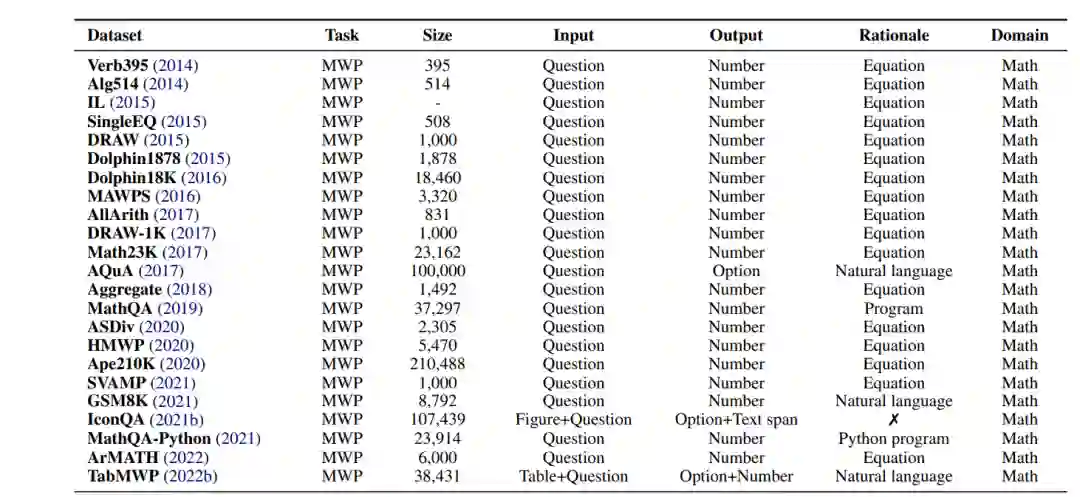
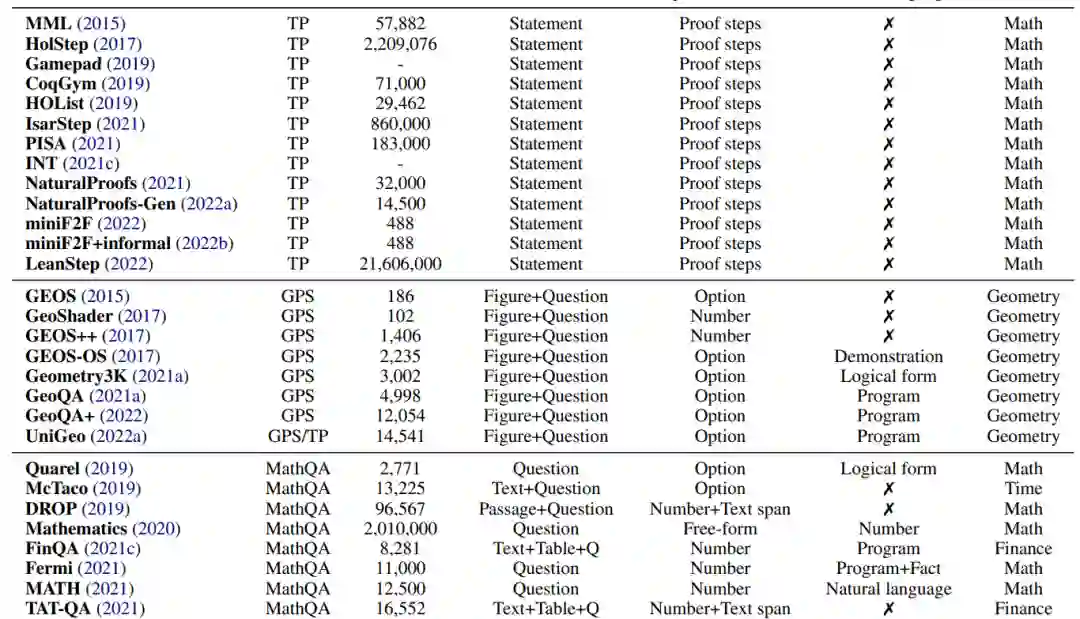
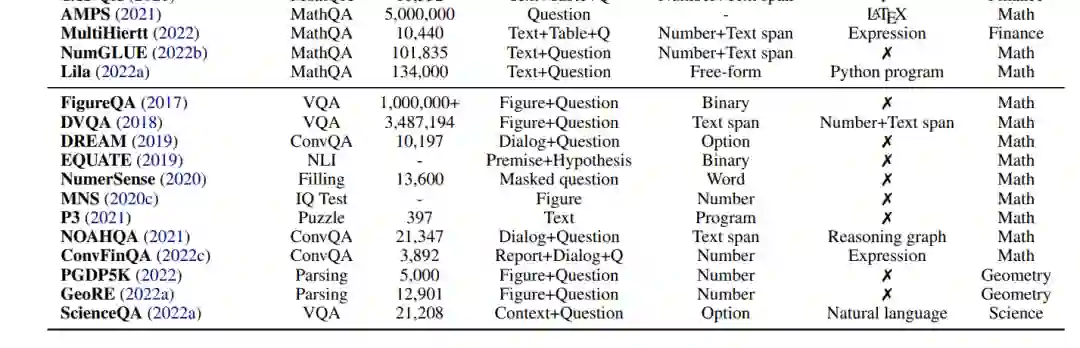
在本节中，我们将研究目前用于使用深度学习方法进行数学推理研究的各种任务和数据集。表2列出了该领域常用的数据集。

2.1 数学应用题解决

几十年来，开发自动解决数学应用题(MWPs)的算法一直是NLP研究人员的兴趣(Feigenbaum et al.， 1963;Bobrow, 1964)。数学应用题(也称为代数或算术应用题)描述了一个简短的叙述，涉及字符、实体和数量。MWP的数学关系可以用一组方程来建模，这些方程的解揭示了问题的最终答案。一个典型的例子如表1所示。作题涉及加、减、乘、除四种基本算术运算，有一个或多个运算步骤。NLP系统中MWPs的挑战在于对语言理解、语义解析和多种数学推理技能的需求。

2.2 定理证明

自动化定理证明是人工智能领域长期以来的挑战(Newell等人，1957;Feigenbaum et al.， 1963)。问题是要通过一系列逻辑论证(证明)来证明一个数学主张(定理)的真实性。定理证明测试了各种技能，例如选择有效的多步策略，使用背景知识和执行符号操作(例如算术或推导)。

2.3 几何解题

自动几何问题求解(GPS)也是数学推理研究中一个长期存在的人工智能任务(Gelernter et al., 1960; Wen-Tsun, 1986; Chou et al., 1996; Ye et al., 2008)，近年来备受关注。与数学应用题不同，几何问题由自然语言的文本描述和几何图形组成。如图2所示，多模态输入描述了几何元素的实体、属性和关系，目标是找到未知变量的数值解。GPS对于深度学习方法来说是一项具有挑战性的任务，因为它需要复杂的技能。它涉及到解析多模态信息、进行符号抽象、利用定理知识和进行定量推理的能力。

2.4 数学问答

数值推理是人类智能中的核心能力，在许多自然语言处理任务中发挥着重要作用。除了定理证明和年级数学应用题解决，还有广泛的以数学推理为中心的问答(QA)基准。本文将这些任务称为数学问答(MathQA)。近年来出现了大量的数据集。例如，QuaRel (Tafjord et al.， 2019)是一个包含不同故事问题的数据集，涉及19种不同类型的数量。McTaco (Zhou et al.， 2019)研究的是时间常识问题，而Fermi (Kalyan et al.， 2021)研究的是费米问题，其答案只能近似估计。

3 用于数学推理的神经网络

3.1 数学的Seq2Seq网络

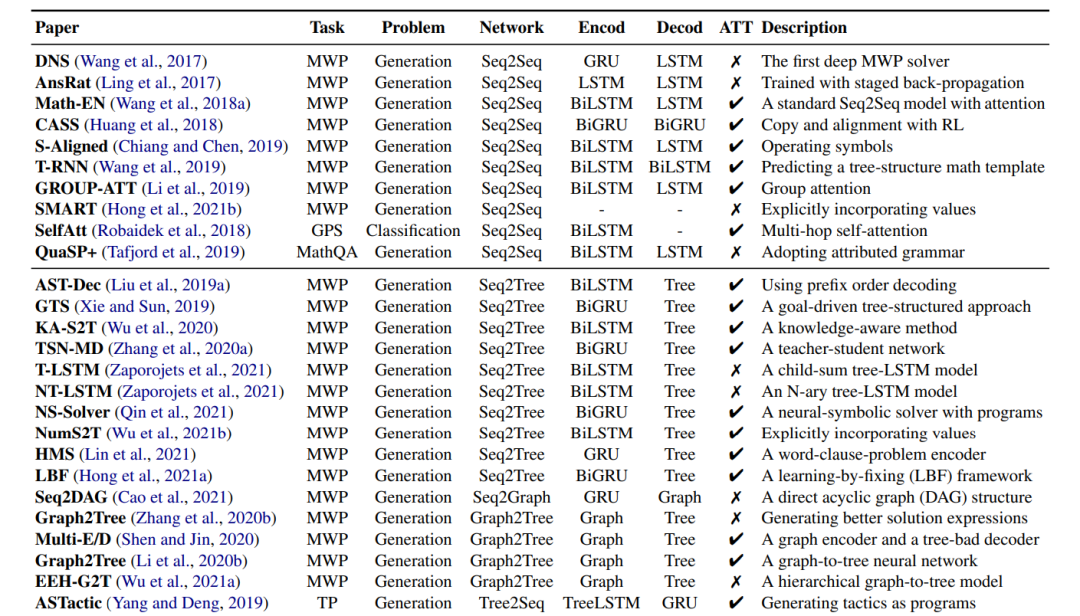
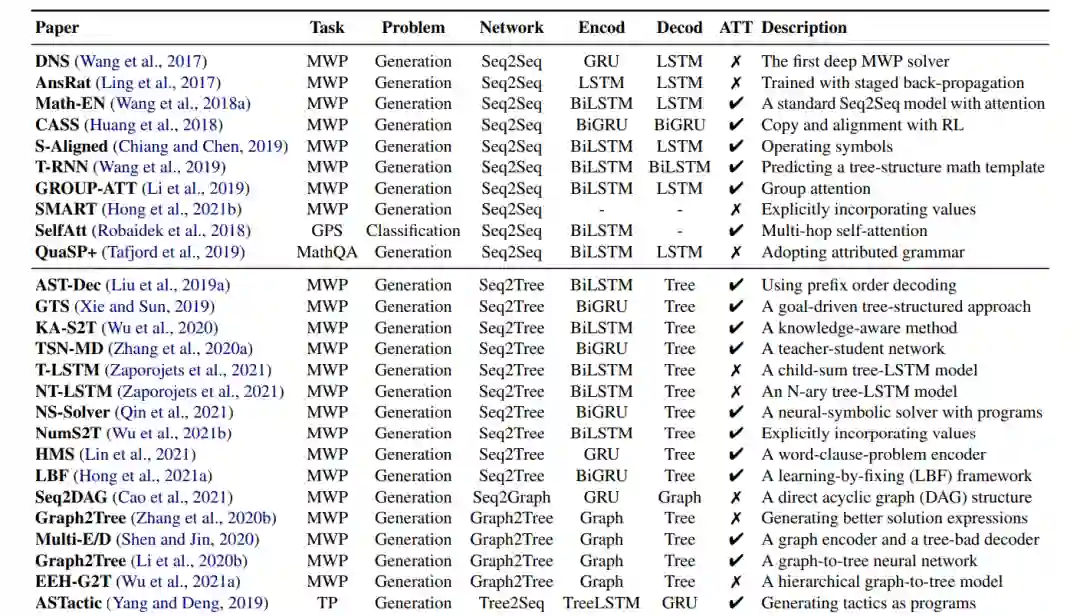
序列到序列(Seq2Seq) (Sutskever et al.， 2014)神经网络已成功应用于数学推理任务，如数学应用题解决(Wang et al.， 2017)、定理证明(Yang and Deng, 2019)、几何问题解决(Robaidek et al.， 2018)和数学问答(Tafjord et al.， 2019)。Seq2Seq模型使用编码器-解码器架构，通常将数学推理形式化为序列生成任务。这种方法背后的基本思想是将输入序列(例如数学问题)映射到输出序列(例如方程、程序和证明)。常见的编码器和解码器包括长短期记忆网络(LSTM) (Hochreiter和Schmidhuber, 1997)、门控循环单元(GRU) (Cho等人，2014)以及它们的双向变体:BiLSTM和BiGRU。DNS (Wang et al.， 2017)是第一项使用Seq2Seq模型将应用题中的句子转换为数学方程的工作。大量工作表明，Seq2Seq模型比之前的统计学习方法具有性能优势(Ling et al., 2017; Wang et al., 2018a; Huang et al., 2018; Chiang and Chen, 2019; Wang et al., 2019; Li et al., 2019)。

3.2基于图的数学网络

Seq2Seq方法在生成数学表达式和不依赖手工特征方面表现出优势。数学表达式可以被转换成一种基于树的结构，例如抽象语法树(AST)和一种基于图的结构，它描述了表达式中的结构化信息。然而，Seq2Seq方法没有显式地对这些重要信息进行建模。为了解决这个问题，基于图的神经网络被开发出来显式地建模表达式中的结构。 序列到树(Seq2Tree)模型在编码输出序列时显式建模树结构(Liu et al., 2019a; Xie and Sun, 2019; Wu et al., 2020; Zhang et al., 2020a; Zaporojets et al., 2021; Qin et al., 2021; Wu et al., 2021b; Lin et al., 2021; Hong et al., 2021a)。例如，(Liu et al.， 2019a)设计了一个Seq2Tree模型，以更好地利用来自方程的AST的信息。相反，Seq2DAG (Cao et al.， 2021)，在生成方程时应用了序列图(Seq2Graph)框架，因为图解码器能够提取多个变量之间的复杂关系。在编码输入的数学序列时，也可以嵌入基于图的信息(Zhang et al., 2020b; Shen and Jin, 2020; Li et al., 2020b; Wu et al., 2021a)。例如，ASTactic (Yang and Deng, 2019)在ast上应用TreeLSTM (Tai et al.， 2015)来表示定理证明的输入目标和前提。 3.3基于注意力的数学网络

注意力机制已成功应用于自然语言处理(Bahdanau等人，2014)和计算机视觉问题(Xu等人，2015;Woo等人，2018)，在解码过程中考虑了输入的隐藏向量。最近，研究人员一直在探索它在数学推理任务中的有用性，因为它可以用来识别数学概念之间最重要的关系。例如，Math-EN (Wang et al.， 2018a)是一个数学应用题解决程序，受益于通过自注意力学习到的长距离依赖信息。基于注意力的方法也被应用于其他数学推理任务，如几何问题求解(Robaidek等人，2018;Chen et al.， 2021a)和定理证明(Yang and Deng, 2019)。人们对各种注意力机制进行了研究，以提取更好的表示，例如Group-ATT (Li et al.， 2019)，它使用不同的多头注意力来提取各种类型的MWP特征，以及图注意力，用于提取知识感知信息(Wu et al.， 2020)。

4 预训练的数学推理语言模型

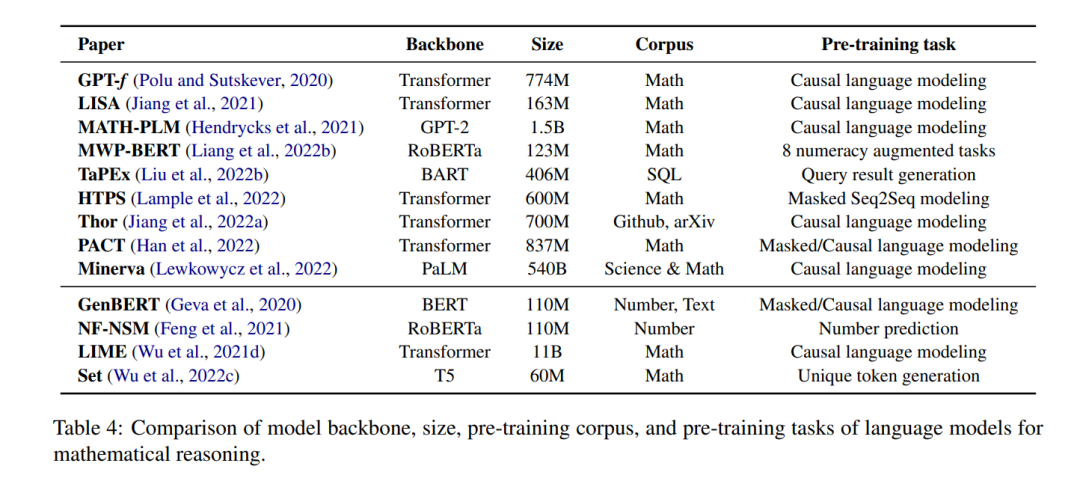
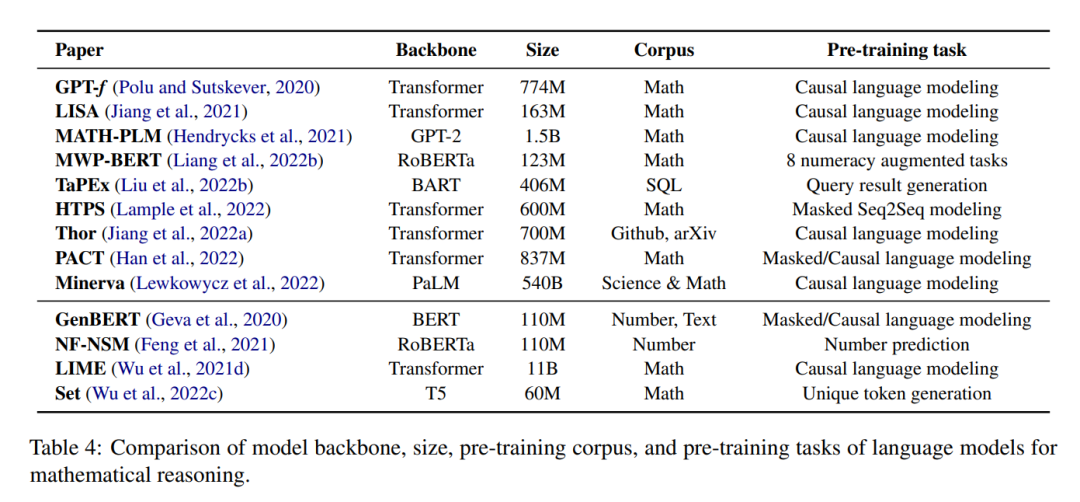
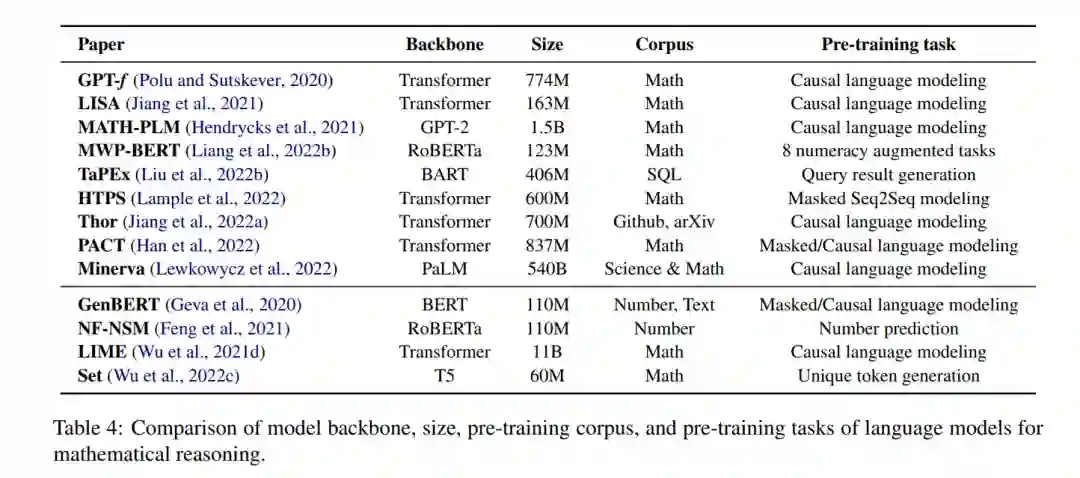
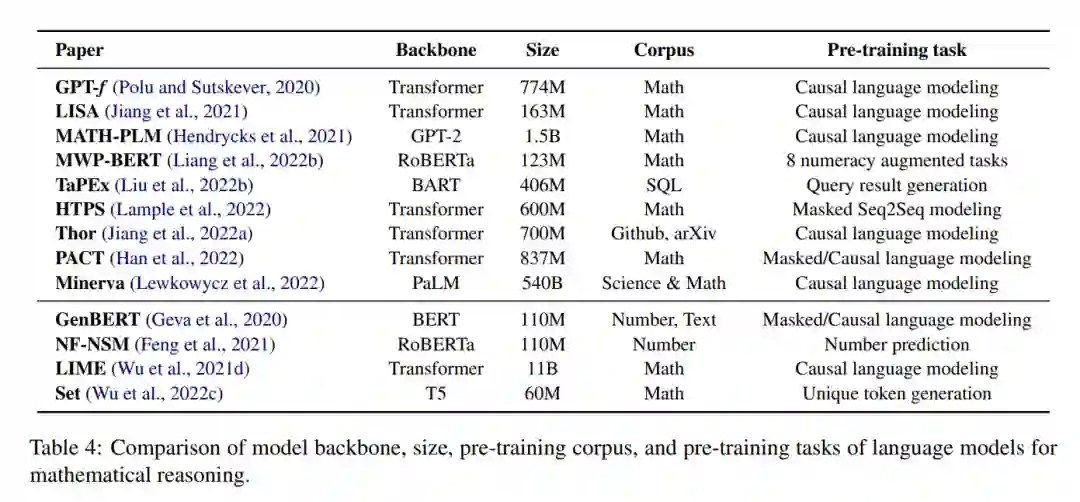
预训练语言模型(例如，Devlin等人(2018);Radford et al. (2020);Brown等人(2020))在广泛的NLP任务上证明了显著的性能提升(Qiu等人，2020)。通过在大型文本语料库上进行预训练，模型学习有价值的世界知识(Guu等人，2020)，这些知识可应用于下游任务，如问题回答(Khashabi等人，2020)、文本分类(Minaee等人，2021)和对话生成(Zhang等人，2019;Qiu等，2022a,b)。类似的想法可以应用于与数学相关的问题，之前的工作表明，预先训练的语言模型在回答数学应用题时表现良好(Kim et al., 2020; Shen et al., 2021; Yu et al., 2021b; Cobbe et al., 2021; Li et al., 2022b; Jie et al., 2022; Ni et al., 2022)，协助定理证明(Polu and Sutskever, 2020; Han et al., 2022; Wu et al., 2022b; Jiang et al., 2022b; Welleck et al., 2022a)，以及其他数学任务(Lu et al., 2021a; Chen et al., 2022a; Cao and Xiao, 2022; Clark et al., 2020; Chen et al., 2021c; Zhu et al., 2021; Hendrycks et al., 2021; Zhao et al., 2022; Nye et al., 2021; Charton, 2021)。

**然而，尽管大型语言模型在建模自然语言方面表现出色，但将其用于数学推理存在一些挑战。**首先，预训练语言模型没有专门在数学数据上进行训练。这可能导致与自然语言任务相比，他们对数学相关任务的熟练程度较低。与文本数据相比，用于大规模预训练的数学或科学数据也较少。其次，预训练模型的规模继续增长，使得为特定的下游任务从头训练整个模型的成本很高。此外，下游任务可能处理不同的输入格式或模态，如结构化表(Zhao et al., 2022; Chen et al., 2021c; Zhu et al., 2021)或图表(Lu et al., 2021a; Chen et al., 2022a; Lu et al., 2021b)。为了应对这些挑战，研究人员必须通过对下游任务进行微调或适应神经架构来调整预训练模型。最后，尽管预训练语言模型可以编码大量的语言信息，但模型仅从语言建模目标中学习数值表示或高级推理技能可能是困难的(Lin et al.， 2020;Kalyan等人，2021年)。考虑到这一点，最近有研究调研了从基础课程开始注入数学相关技能(Geva et al., 2020; Feng et al., 2021; Wu et al., 2021d)。

5 .基于上下文的数学推理学习

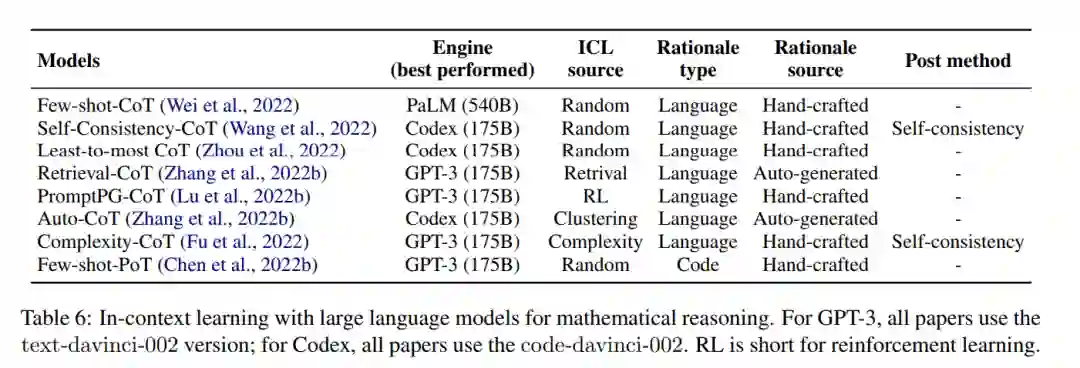
大型语言模型(LLM)，如GPT3 (Brown et al.， 2020)，最近彻底改变了自然语言处理(NLP)领域，特别是由于其强大的少样本上下文学习能力(Brown et al.， 2020)。上下文学习(ICL)使LLM能够通过在推理时提供一些任务示例作为条件来执行目标任务，而无需更新模型参数(Radford et al., 2020; Brown et al., 2020)。ICL允许用户快速为新用例构建模型，而无需担心为每个任务进行微调和存储大量新参数，因此现在被广泛用于少样本设置(Min等人，2022)。一个上下文中的例子通常包含一个输入-输出对和一些提示词，例如，请从列表中选择最大的数字。输入:[2,4,1,5,8]。输出:8，而few-shot通过给出多个示例来工作，然后是一个最终输入示例，模型预计将预测输出。然而，这种标准的少次提示(在测试时示例前给LLM提供输入-输出对的上下文示例)尚未被证明足以在数学推理等具有挑战性的任务上取得高性能(Rae等人，2021)。

结论：

本文对数学推理的深度学习进行了全面的综述。回顾了已经使用的各种任务和数据集，并讨论了已经采取的各种方法，包括早期的神经网络，后来的预训练语言模型和最近的大型语言模型。还确定了现有数据集和方法中的几个差距，包括对低资源设置的关注有限、计算能力表示不足和推理能力不一致。最后，对未来的研究方向进行了展望，并指出了该领域进一步探索的潜力。本文的目标是为对发展数学推理深度学习感兴趣的读者提供一个全面而有用的资源。为了帮助我们完成这项工作，我们创建了一个阅读列表，并将在https://github.com/lupantech/dl4math的GitHub存储库中不断更新