近年来,连续表示方法作为一种新兴范式逐渐兴起,其通过函数表示将位置坐标映射到连续空间中的对应取值,从而刻画真实世界数据的内在结构。相比传统的离散框架,连续表示框架在数据表达与重建(如图像修复、新视角合成、波形反演等)中展现出内在优势,包括分辨率灵活性、跨模态适应性、内在平滑性与参数高效性等。 在本综述中,我们系统回顾了近年来连续表示框架的研究进展,聚焦于以下三个方面: 1. 连续表示方法设计:涵盖基函数表示、统计建模、张量函数分解以及隐式神经表示等; 1. 连续表示的理论基础:包括逼近误差分析、收敛性研究以及隐式正则化机制; 1. 连续表示的实际应用:来自计算机视觉、计算机图形学、生物信息学以及遥感等领域的应用实例。
此外,我们还展望了未来研究方向,旨在激发更深入的探索与理解,进一步推动连续表示方法、理论与应用的发展。 所有参考文献与资源整理于我们的开源仓库中:https://github.com/YisiLuo/Continuous-Representation-Zoo 关键词:连续表示、隐式神经表示、张量分解、压缩感知、优化、收敛性与泛化能力
1 引言
在大数据时代,从不完整测量、噪声观测或物理规则与属性中重建高质量数据仍是多个领域中的基本挑战 [37, 64, 103, 122],例如医学成像重建 [111]、卫星遥感 [63]、图形学中的场景重建 [131],以及数值科学计算 [80]。传统的数据重建方法通常依赖于基于离散网格的表示(如向量、矩阵或高阶张量 [83])和手工设计的先验知识(如稀疏性或低秩性 [185]),这类方法在刻画复杂现实世界数据的内在几何或拓扑结构方面往往存在局限。尤其在处理如任意分辨率成像 [20]、三维医学图像配准 [11]、图形重建 [131]、雷达成像几何 [26]、不规则空间转录组数据 [28]等不规则采样、模态异质或跨分辨率任务时,这些问题更加突出。 为应对上述挑战,连续表示方法(参考经典工作 [20,103,105,110,134,157])作为一种变革性范式,正在广泛应用于通用数据重建问题中。连续表示指的是:利用连续函数表示来建模离散数据,通过参数模型(如基函数或深度神经网络)将位置坐标(例如空间位置、时间索引或视角方向)映射到对应的响应值(如图像像素、物理场或体积强度)。 为了增强连续表示的有效性,可以通过引入隐式或显式结构约束对表示函数进行正则化,例如损失函数中的微分算子 [10] 或函数分解 [103]。将离散数据嵌入到这样一种平滑、分辨率无关的连续空间后,这些方法具备诸多优势,包括全局特征建模、对不规则多维数据的适应性、分辨率无关性以及可解释的学习理论等。例如,隐式神经表示(INRs) [20, 134, 142] 通过神经网络将信号参数化为连续函数,从而实现无缝插值与超分辨率;张量函数分解框架 [42,103] 通过多元函数的低秩因式分解挖掘高维数据的多线性结构;统计型连续表示方法 [17,40,42] 编码了时间连续域中的相关性,适用于流数据或时间序列分析。 这类连续方法天然避免了离散化误差,具备高度参数效率——离散数据可以由参数量远少于原始数据规模的模型所表示。这一特性在大规模数据任务中尤为重要,例如 5D 地震数据插值 [48] 或视频时空超分辨率 [22]。此外,连续表示还易于整合领域先验知识,如:在全波形反演中引入物理约束 [35],或在磁共振成像(MRI)中引入准静态运动先验 [159],从而弥合通用模型与应用需求之间的鸿沟。总之,连续表示方法正日益成为多类数据重建任务中的有效研究范式。 尽管进展迅速,该领域仍存在明显的碎片化现象。现有研究往往聚焦于某一特定方向,如:通用方法设计(如函数的切比雪夫展开 [60]、傅里叶特征 INRs [142]、小波 INRs [129])、理论分析(如神经切线核理论 [2, 72, 142] 或隐式正则化视角下的收敛性研究 [58, 103]),或某些具体应用(如连续高光谱成像 [14]、可变形配准 [11]、偏微分方程的函数分解求解 [146]),而缺乏对它们之间交叉关联的系统整合。事实上,这种交叉联系对于加深理解与推进创新至关重要。 例如,广泛研究的基于 INR 的任意尺度图像超分辨率 [20],其训练范式与神经算子方法 [84,96] 本质相似——两者均以低维输入(坐标或潜在变量)生成高分辨率输出。又如,用于三维场景重建的张量辐射场 [13],在科学计算中本质上与张量函数分解方法 [51,60,103,137] 存在内在联系。再如,经典的傅里叶基函数表示 [80] 与近年来融合傅里叶基的神经表示方法 [142] 在原理上也具有一致性。
本文主要目标
本综述旨在系统梳理连续表示方法的理论基础、方法设计与应用实践,包括: * 各类连续参数模型与结构建模方法; * 连续方法的数学性质与理论框架(如逼近误差、收敛性等); * 以及其在医学影像、遥感、生物信息等多个具体领域的实际应用。
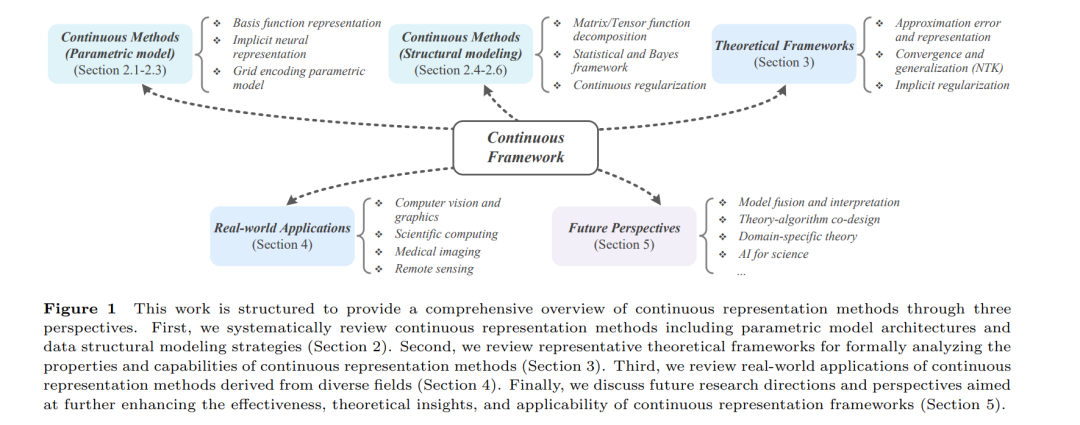
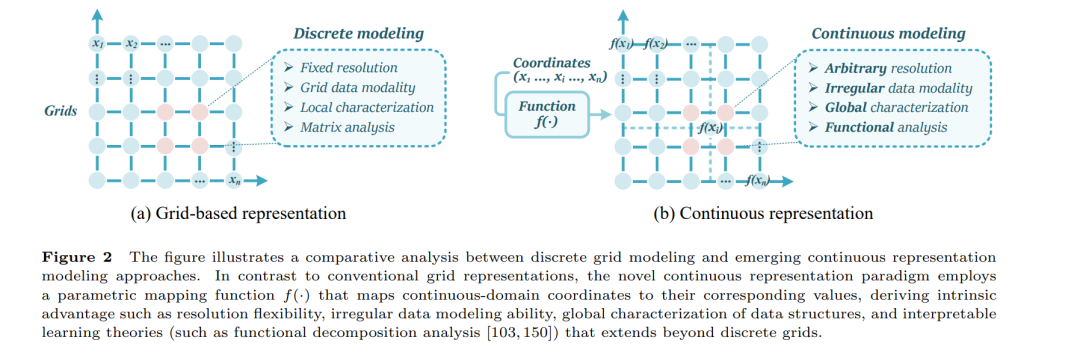
我们希望借此填补该领域不同子方向之间的信息鸿沟,激发新的交叉研究与应用探索。 图 1 总结了本文所介绍的连续表示方法、理论与应用的研究进展;图 2 则直观展示了该类方法的基本概念与优势。
本文主要贡献如下:
系统综述:围绕连续表示方法的设计、理论洞见与跨领域应用三方面,系统梳理其在数据表示与重建中的研究进展,揭示其在相关领域的快速演进轨迹; * 前瞻展望:提出未来具有潜力的研究方向,回应当前连续方法设计、理论发展与应用拓展中的关键挑战,促进跨学科协作,推动数据重建方法的进一步发展。
文章结构安排:
第 2 节:回顾各种连续表示模型与结构建模方法的发展; * 第 3 节:深入探讨连续表示方法的理论基础,如逼近误差分析与神经切线核理论; * 第 4 节:梳理其在医学成像、遥感、生物信息等应用场景中的实践成果; * 第 5 节:展望未来研究方向,激发对连续表示方法的进一步探索。