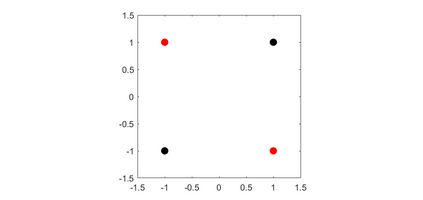
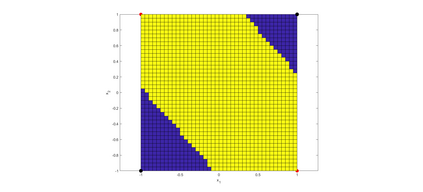
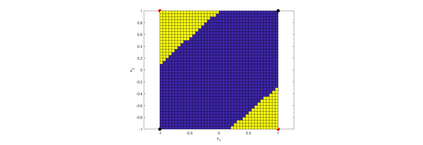
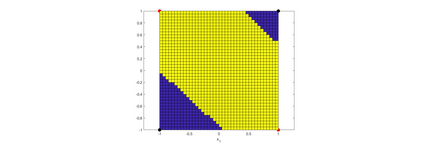
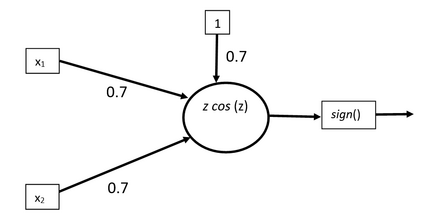
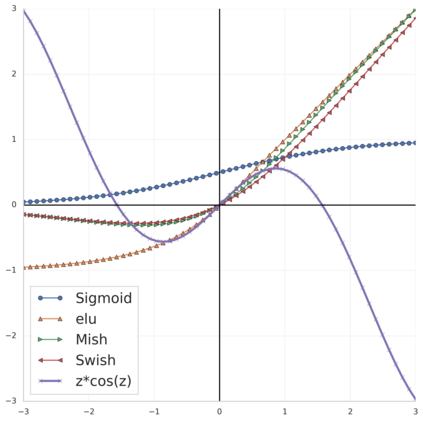
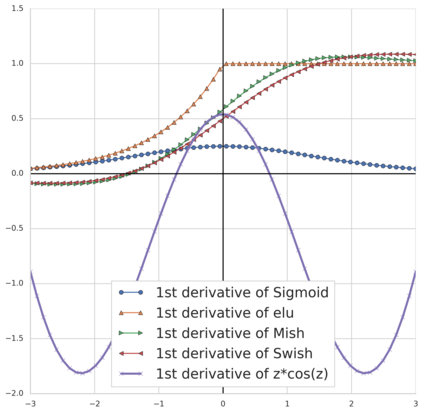
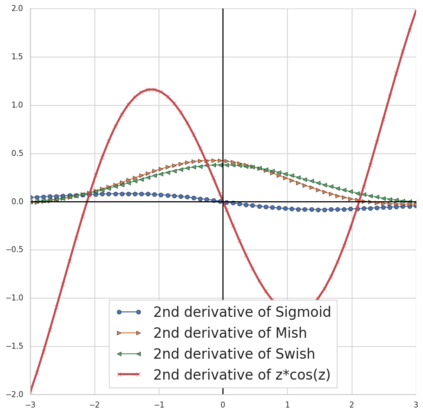
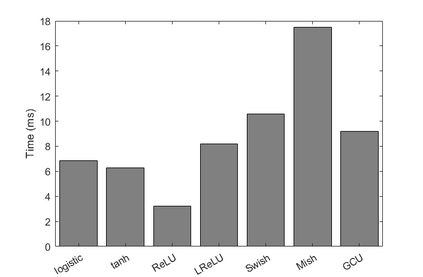
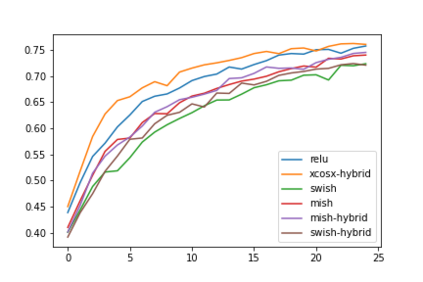
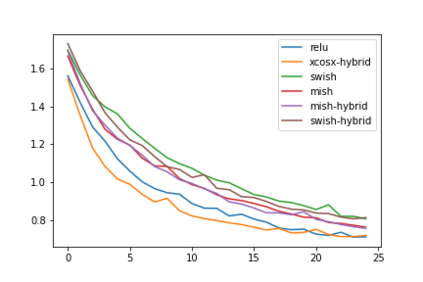
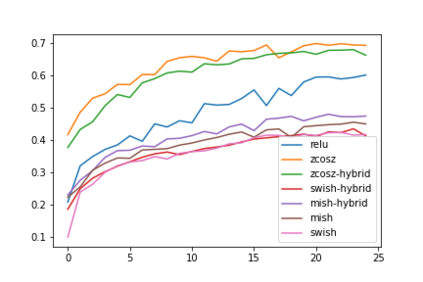
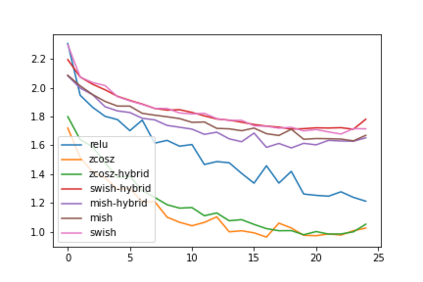
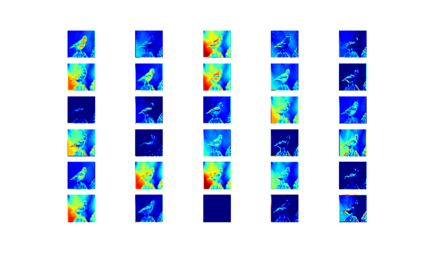
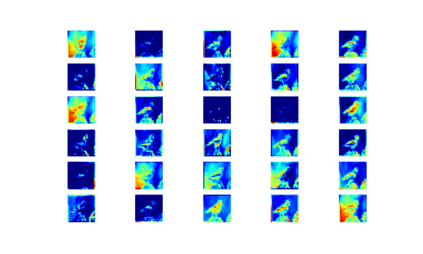
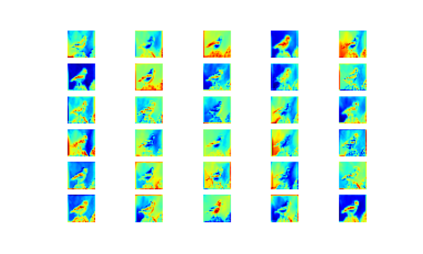
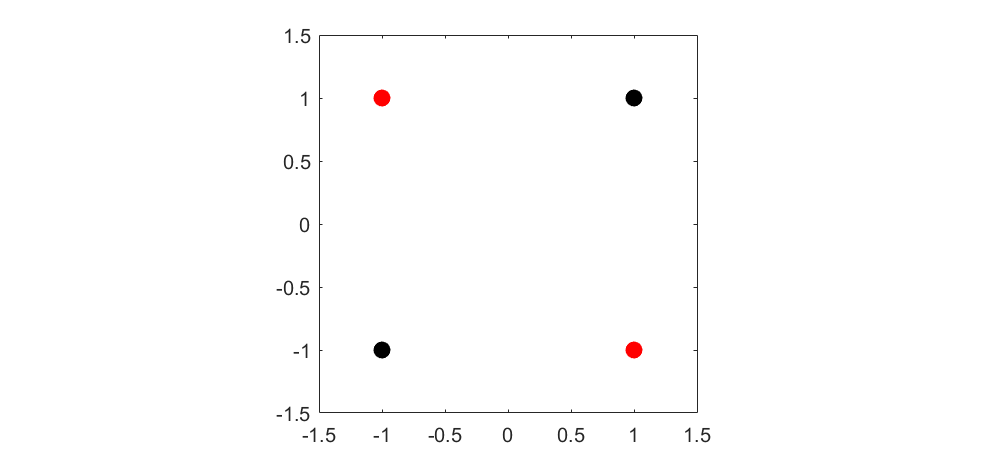
Convolution neural networks have been successful in solving many socially important and economically significant problems. Their ability to learn complex high-dimensional functions hierarchically can be attributed to the use of nonlinear activation functions. A key discovery that made training deep networks feasible was the adoption of the Rectified Linear Unit (ReLU) activation function to alleviate the vanishing gradient problem caused by using saturating activation functions. Since then many improved variants of the ReLU activation have been proposed. However a majority of activation functions used today are non-oscillatory and monotonically increasing due to their biological plausibility. This paper demonstrates that oscillatory activation functions can improve gradient flow and reduce network size. It is shown that oscillatory activation functions allow neurons to switch classification (sign of output) within the interior of neuronal hyperplane positive and negative half-spaces allowing complex decisions with fewer neurons. A new oscillatory activation function C(z) = z cos z that outperforms Sigmoids, Swish, Mish and ReLU on a variety of architectures and benchmarks is presented. This new activation function allows even single neurons to exhibit nonlinear decision boundaries. This paper presents a single neuron solution to the famous XOR problem. Experimental results indicate that replacing the activation function in the convolutional layers with C(z) significantly improves performance on CIFAR-10, CIFAR-100 and Imagenette.
翻译:革命神经网络成功地解决了许多具有社会重要性和经济重要性的问题。 它们从等级上学习复杂高维功能的能力可以归因于使用非线性激活功能。 使深网络培训成为可行的一项关键发现是采用了校正线性单元(RELU)激活功能,以缓解因使用饱和激活功能而消失的梯度问题。 从那时以来,提出了许多经改进的RELU激活变体。 但是,今天使用的大多数激活功能由于生物光学性,是非螺旋和单质增加的。本文表明,悬浮激活功能可以改善梯度流并缩小网络规模。 一项关键发现,使深线性启动功能允许神经神经元在神经超平面正反反半空内部转换分类(输出),从而能够以较少的神经元来做出复杂的决定。 一个新的骨质激活功能C(z) = z z z, 超越了图像直径、 Swish、 Mish 和 ReLU, 显示, 系统激活功能可以改进梯度的梯度流和 直径直线 的神经级模型和直径直径直径直径直径直径 。 显示, 的直径直径直径直径直径直线性功能可以显示单一直为单一的图像的图像显示的直径直线。