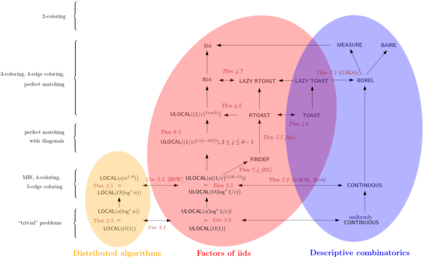
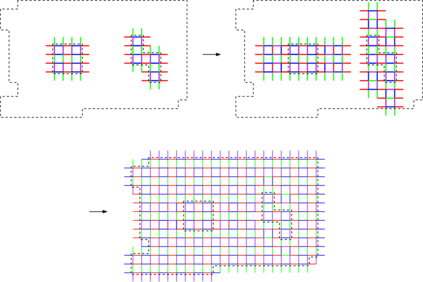We present an intimate connection among the following fields: (a) distributed local algorithms: coming from the area of computer science, (b) finitary factors of iid processes: coming from the area of analysis of randomized processes, (c) descriptive combinatorics: coming from the area of combinatorics and measure theory. In particular, we study locally checkable labellings in grid graphs from all three perspectives. Most of our results are for the perspective (b) where we prove time hierarchy theorems akin to those known in the field (a) [Chang, Pettie FOCS 2017]. This approach that borrows techniques from the fields (a) and (c) implies a number of results about possible complexities of finitary factor solutions. Among others, it answers three open questions of [Holroyd et al. Annals of Prob. 2017] or the more general question of [Brandt et al. PODC 2017] who asked for a formal connection between the fields (a) and (b). In general, we hope that our treatment will help to view all three perspectives as a part of a common theory of locality, in which we follow the insightful paper of [Bernshteyn 2020+] .
翻译:我们展示了以下领域的紧密联系:(a) 分布式本地算法:(a) 分布式本地算法:来自计算机科学领域的本地算法;(b) iid过程的原始因素:来自随机化过程分析领域;(c) 描述性组合法:(c) 描述性组合法:来自组合法和测量理论领域;特别是,我们从所有三个角度研究网格图中的可本地核对标签;我们的大多数结果都来自以下角度:(b) 我们证明时间等级的标语类似于实地已知的标语(a) [Chang, Pettie FOCS 2017];这种方法从领域借用技术(a) 和(c) 意味着关于氟化因素解决方案可能的复杂性的若干结果;除其他外,它回答了[Holroud et al. Annals of Prob. 201717] 三个公开的问题,或更笼统的[Brandt et al. POCDC 2017] 问题,他们要求将领域(a)和(b) 正式连接起来。我们希望我们的处理方法将有助于将所有三个观点视为2020年共同理论的一部分。