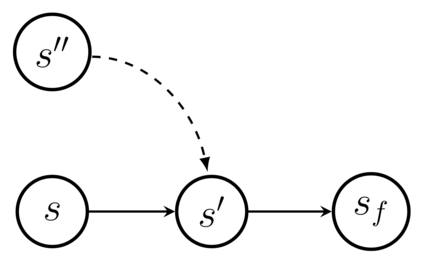
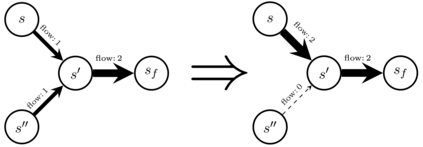
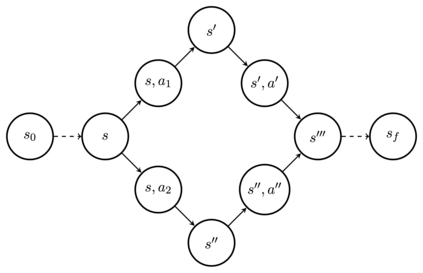
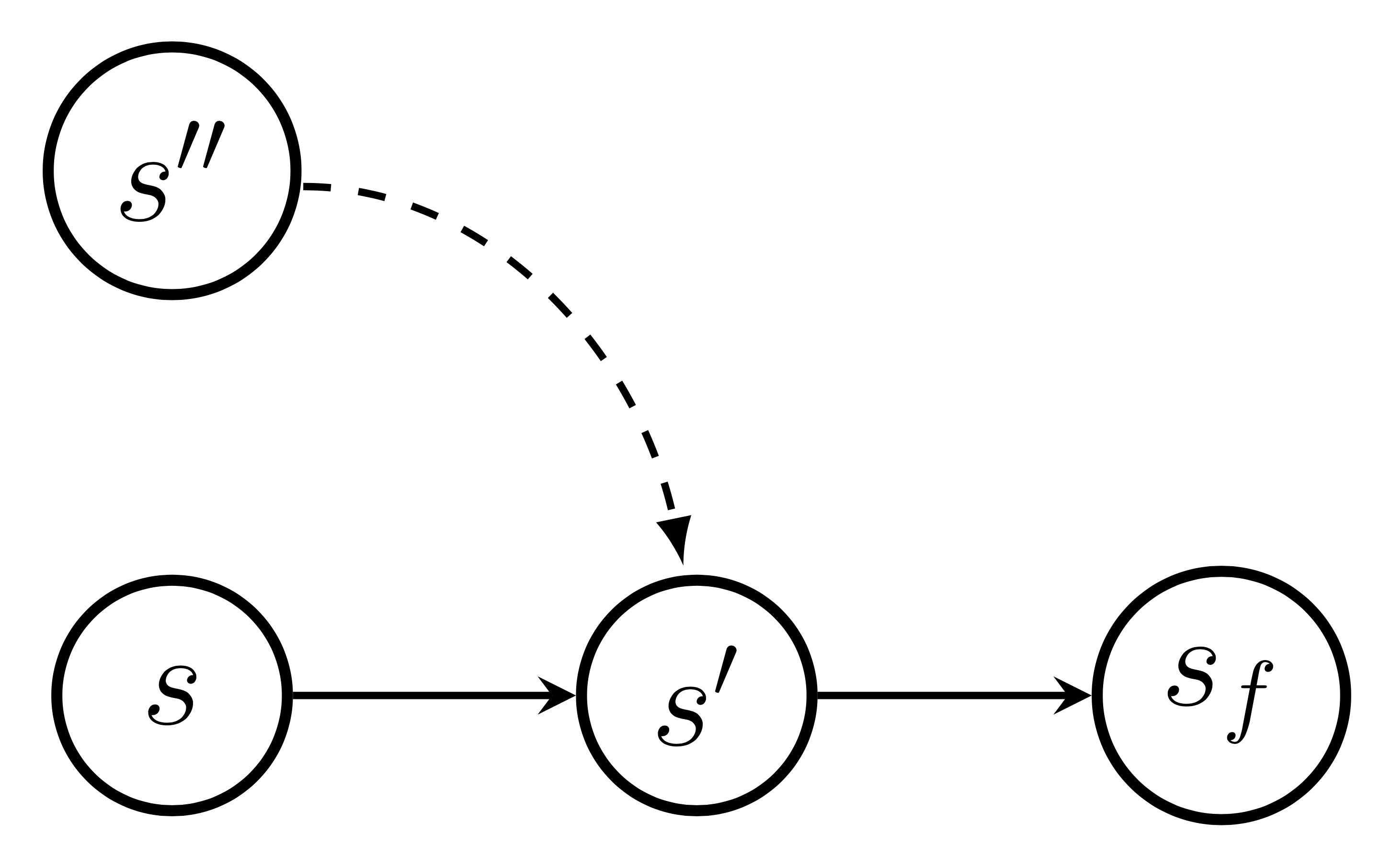
Generative Flow Networks (GFlowNets) have been introduced as a method to sample a diverse set of candidates in an active learning context, with a training objective that makes them approximately sample in proportion to a given reward function. In this paper, we show a number of additional theoretical properties of GFlowNets. They can be used to estimate joint probability distributions and the corresponding marginal distributions where some variables are unspecified and, of particular interest, can represent distributions over composite objects like sets and graphs. GFlowNets amortize the work typically done by computationally expensive MCMC methods in a single but trained generative pass. They could also be used to estimate partition functions and free energies, conditional probabilities of supersets (supergraphs) given a subset (subgraph), as well as marginal distributions over all supersets (supergraphs) of a given set (graph). We introduce variations enabling the estimation of entropy and mutual information, sampling from a Pareto frontier, connections to reward-maximizing policies, and extensions to stochastic environments, continuous actions and modular energy functions.
翻译:在积极学习的背景下,引入了多种生成流程网络(GFlowNets),作为一种方法,对各类候选人进行抽样抽样,其培训目标是使其与特定奖赏功能成比例的大致抽样。在本文件中,我们展示了GFlowNets的其他一些理论属性。这些理论属性可用于估算共同概率分布和相应的边际分布,其中某些变量没有说明,特别令人感兴趣的是,这些变量可以代表组合物体(如数据集和图)的分布。 GFlowNets将通常通过计算昂贵的MCMC方法在单一但经过培训的基因传承中完成的工作进行摊合,还可以用于估算分割功能和自由能量、给给给某一集(子类)的超集(超级图)的有条件概率(超级图)以及所有超集(超级图)的边际分布。我们引入了各种变化,以便估算昆虫和相互信息,从Pareto边界取样,与奖励-maximmizing 政策的联系,以及扩展到随机环境、连续行动和模块能源功能。