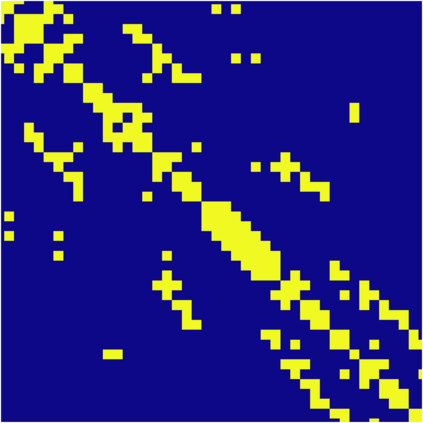
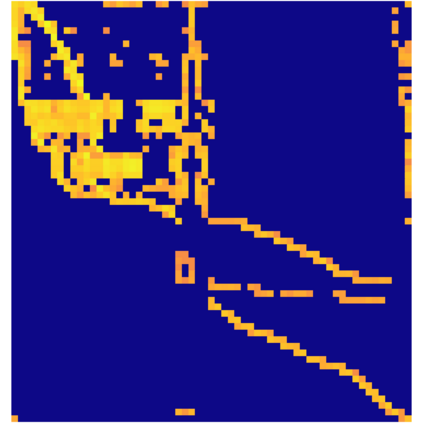
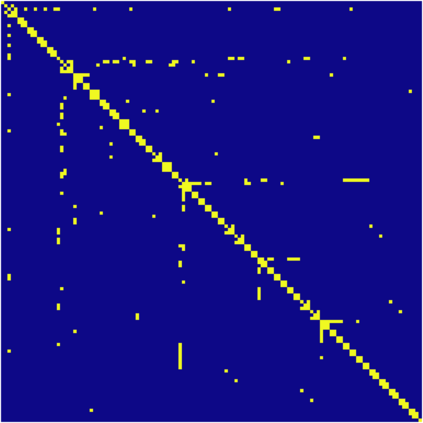
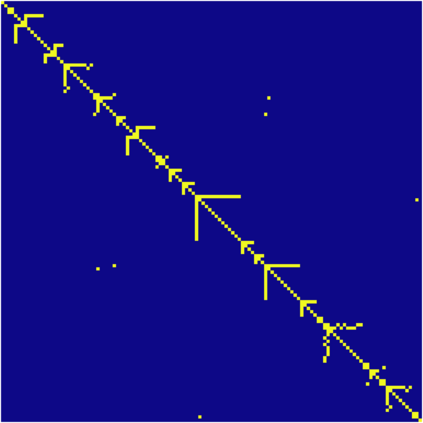
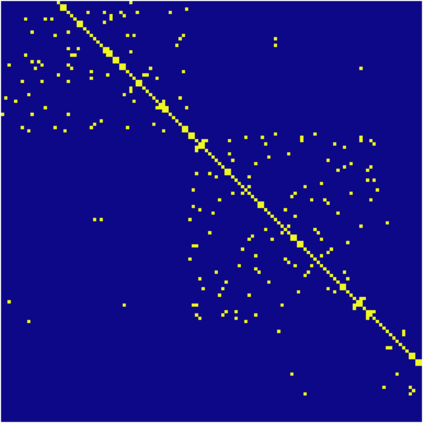
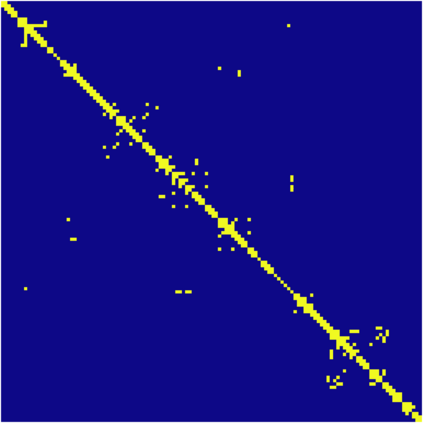
The Variable Block Row (VBR) format is an influential blocked sparse matrix format designed for matrices with shared sparsity structure between adjacent rows and columns. VBR groups adjacent rows and columns, storing the resulting blocks that contain nonzeros in a dense format. This reduces the memory footprint and enables optimizations such as register blocking and instruction-level parallelism. Existing approaches use heuristics to determine which rows and columns should be grouped together. We show that finding the optimal grouping of rows and columns for VBR is NP-hard under several reasonable cost models. In light of this finding, we propose a 1-dimensional variant of VBR, called 1D-VBR, which achieves better performance than VBR by only grouping rows. We describe detailed cost models for runtime and memory consumption. Then, we describe a linear time dynamic programming solution for optimally grouping the rows for 1D-VBR format. We extend our algorithm to produce a heuristic VBR partitioner which alternates between optimally partitioning rows and columns, assuming the columns or rows to be fixed, respectively. Our alternating heuristic produces VBR matrices with the smallest memory footprint of any partitioner we tested.
翻译:变量块列( VBR) 格式是用于相邻行和列之间具有共享宽度结构的矩阵的有影响力的封闭性稀释矩阵格式。 VBR 组群相邻的行和列, 以密集格式储存含有非零的区块。 这会减少记忆足迹, 并允许优化, 如注册封隔和教学级平行。 现有方法使用惯性来决定哪些行和列应该组合在一起。 我们显示, 找到VBR 最佳的行和列组是几个合理成本模型下的 NP- 硬化的。 根据这一发现, 我们建议 VBR 1 的一维变量, 称为 1D- VBR, 其性能优于 VBR 。 我们描述运行时间和记忆消耗的详细成本模型。 然后, 我们描述一个以 1D- VBR 格式优化组合行的线性时间动态编程解决方案。 我们扩展了算法, 以产生一种超常性 VBR 的 VBR 隔行和列之间互换的 VBR 。, 假设列或行将分别固定的列, 我们的循环的 Heuristimalmissmost 将产生任何最小的VBRM 基质平基质的VBR 。