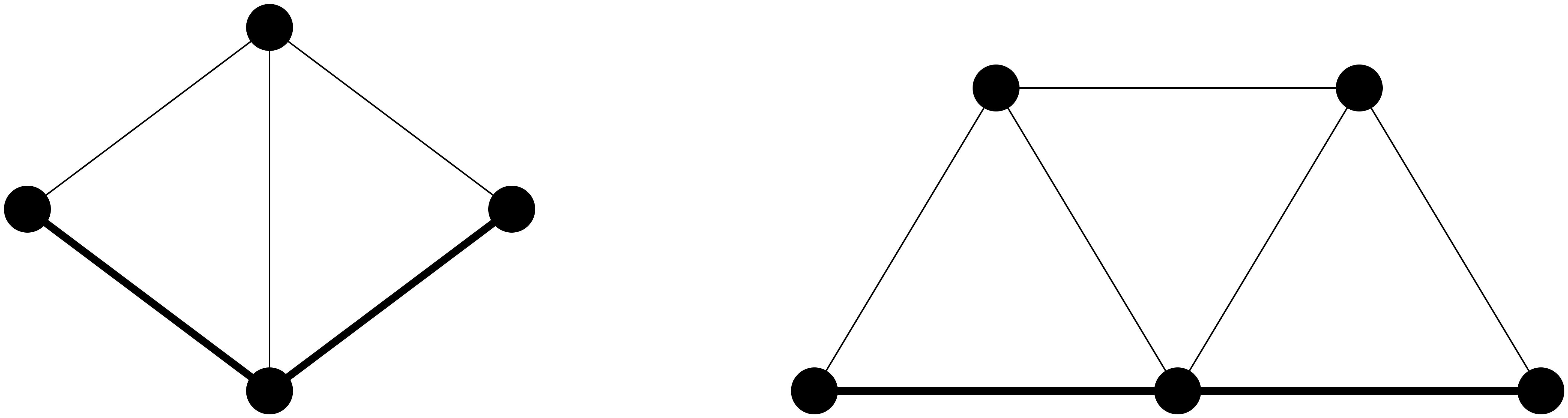
A \textit{biclique} is a maximal induced complete bipartite subgraph. The \textit{biclique graph} of a graph $H$, denoted by $KB(H)$, is the intersection graph of the family of all bicliques of $H$. In this work we address the following question: Given a biclique graph $G=KB(H)$, is it possible to remove a vertex $q$ of $G$, such that $G - \{q\}$ is a biclique graph? And if possible, can we obtain a graph $H'$ such that $G - \{q\} = KB(H')$? We show that the general question has a "no" for answer. However, we prove that if $G$ has a vertex $q$ such that $d(q) = 2$, then $G-\{q\}$ is a biclique graph and we show how to obtain $H'$.
翻译:\ textit{ biclique} 是一个最大引导的完整的双面子图。 由 $KB( H) 表示的 $ 的 美元 图表 的\ textit{ biclique 图形 。 如果可能的话, 我们能得到 $H 的 美元 的 美元 图表 。 我们显示一般问题有一个 “ 不 ” 的答案 。 但是, 我们证明, 如果 $G 有 everex $G = 2 美元, 那么$G - Q Q $ 是一个 biclique 的 图表, 我们如何获得 $H 美元 。