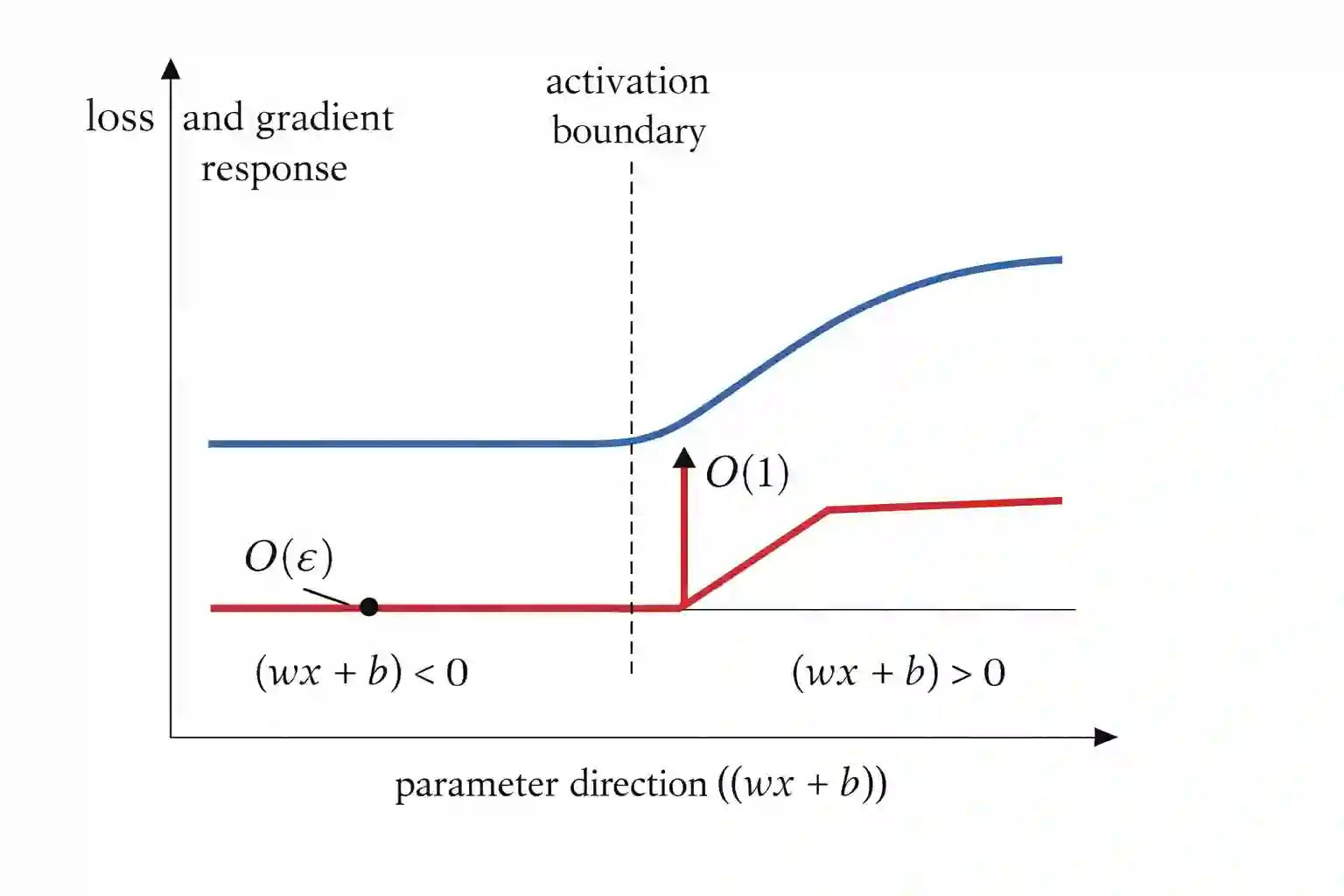
Stability analyses of modern learning systems are frequently derived under smoothness assumptions that are violated by ReLU-type nonlinearities. In this note, we isolate a minimal obstruction by showing that no uniform smoothness-based stability proxy such as gradient Lipschitzness or Hessian control can hold globally for ReLU networks, even in simple settings where training trajectories appear empirically stable. We give a concrete counterexample demonstrating the failure of classical stability bounds and identify a minimal generalized derivative condition under which stability statements can be meaningfully restored. The result clarifies why smooth approximations of ReLU can be misleading and motivates nonsmooth-aware stability frameworks.
翻译:现代学习系统的稳定性分析通常基于平滑性假设,而ReLU型非线性函数会违反这些假设。本文指出一个根本性障碍:即使是在训练轨迹经验上表现稳定的简单场景中,ReLU网络也无法全局满足基于均匀平滑性的稳定性代理条件(如梯度Lipschitz连续性或Hessian控制)。我们通过具体反例证明经典稳定性界限的失效,并确定一个最小广义导数条件,使得稳定性结论能够被有意义地恢复。该结果阐明了ReLU的平滑近似为何可能产生误导,并推动建立非平滑感知的稳定性分析框架。