IETI-DP methods for discontinuous Galerkin multi-patch Isogeometric Analysis with T-junctions

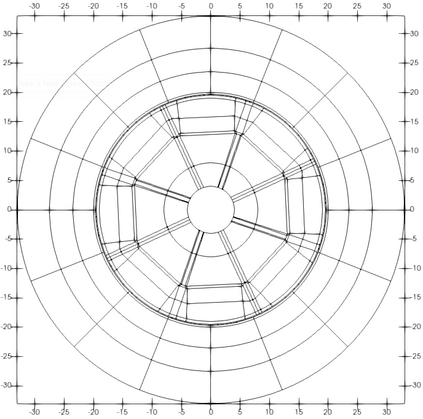
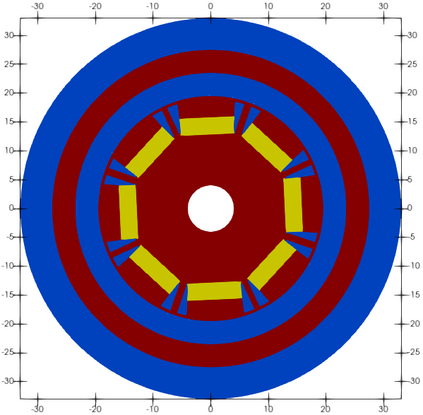
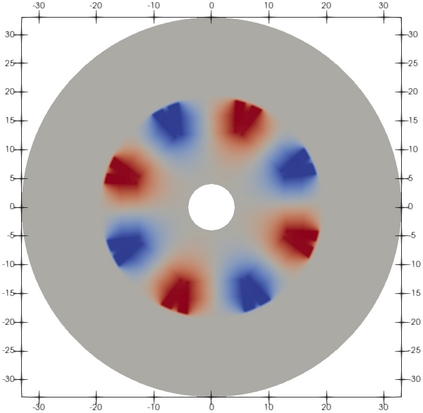
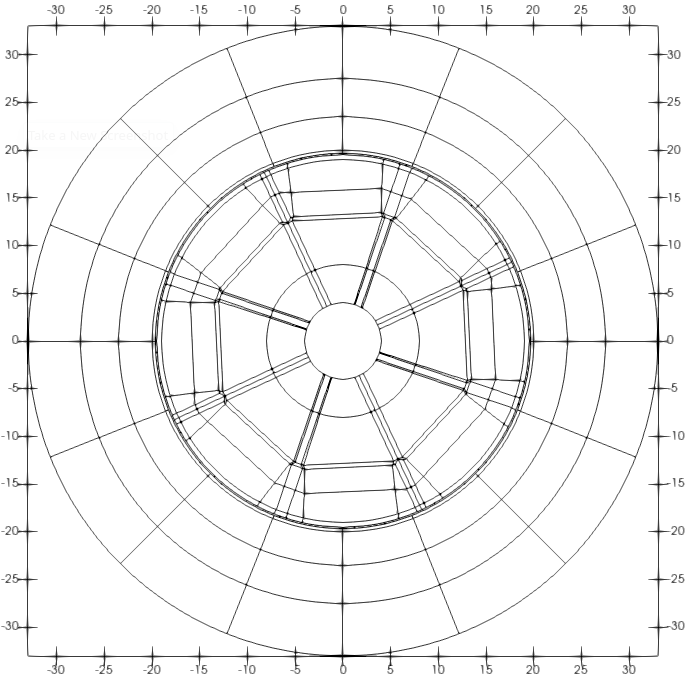
We study Dual-Primal Isogeometric Tearing and Interconnecting (IETI-DP) solvers for non-conforming multi-patch discretizations of a generalized Poisson problem. We realize the coupling between the patches using a symmetric interior penalty discontinuous Galerkin (SIPG) approach. Previously, we have assumed that the interfaces between patches always consist of whole edges. In this paper, we drop this requirement and allow T-junctions. This extension is vital for the consideration of sliding interfaces, for example between the rotor and the stator of an electrical motor. One critical part for the handling of T-junctions in IETI-DP solvers is the choice of the primal degrees of freedom. We propose to add all basis functions that are non-zero at any of the vertices to the primal space. Since there are several such basis functions at any T-junction, we call this concept ''fat vertices''. For this choice, we show a condition number bound that coincides with the bound for the conforming cas