Optimizing Ansatz Design in QAOA for Max-cut

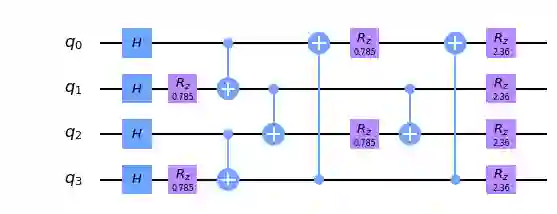
Quantum Approximate Optimization Algorithm (QAOA) has been studied widely in the literature, primarily for finding an approximate value of the maximum cut size of a graph. QAOA is composed of a problem hamiltonian and a mixer hamiltonian which are applied alternately for $p \geq 1$ layers. The circuit for this algorithm requires $2m$ CNOT gates in each layer, where $m$ is the number of edges in the graph. CNOT gate is one of the primary sources of error in modern quantum computers. In this paper, we propose two techniques for reducing the number of CNOT gates in the circuit which are independent of the hardware architecture. For a graph with $n$ vertices, we first propose a technique based on edge coloring that can reduce upto $\lfloor \frac{n}{2} \rfloor$ CNOT gates in the circuit. Next, we propose another technique based on Depth First Search (DFS) that can reduce $n-1$ CNOT gates at the cost of some increased depth. We analytically derive the criteria for which the reduction in the number of CNOT gates due to the DFS based technique can provide lower error probability even with some increased depth, and show that all graphs conform to this criteria, making this technique universal. We further show that this proposed optimization holds even in the post transpilation stage of the circuit, which is actually executed in the IBM Quantum hardware. We simulate these two techniques for graphs of various sparsity with the ibmq_manhattan noise model and show that the DFS based technique outperforms the edge coloring based technique, which in turn, outperforms the traditional QAOA circuit in terms of reduction in the number of CNOT gates, and hence the probability of error of the circuit.