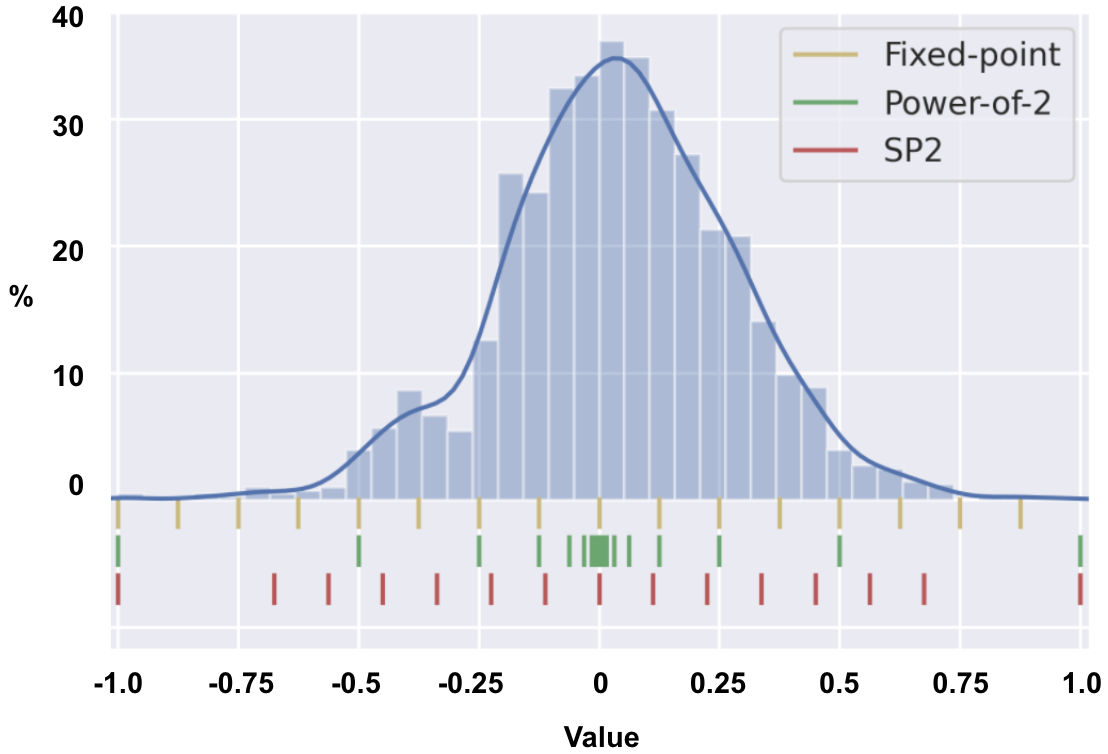
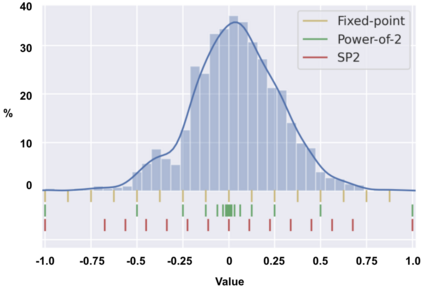
Deep Neural Networks (DNNs) have achieved extraordinary performance in various application domains. To support diverse DNN models, efficient implementations of DNN inference on edge-computing platforms, e.g., ASICs, FPGAs, and embedded systems, are extensively investigated. Due to the huge model size and computation amount, model compression is a critical step to deploy DNN models on edge devices. This paper focuses on weight quantization, a hardware-friendly model compression approach that is complementary to weight pruning. Unlike existing methods that use the same quantization scheme for all weights, we propose the first solution that applies different quantization schemes for different rows of the weight matrix. It is motivated by (1) the distribution of the weights in the different rows are not the same; and (2) the potential of achieving better utilization of heterogeneous FPGA hardware resources. To achieve that, we first propose a hardware-friendly quantization scheme named sum-of-power-of-2 (SP2) suitable for Gaussian-like weight distribution, in which the multiplication arithmetic can be replaced with logic shifter and adder, thereby enabling highly efficient implementations with the FPGA LUT resources. In contrast, the existing fixed-point quantization is suitable for Uniform-like weight distribution and can be implemented efficiently by DSP. Then to fully explore the resources, we propose an FPGA-centric mixed scheme quantization (MSQ) with an ensemble of the proposed SP2 and the fixed-point schemes. Combining the two schemes can maintain, or even increase accuracy due to better matching with weight distributions.
翻译:深神经网络(DNN) 在不同应用领域取得了非凡的绩效。 为支持不同的 DNN 模型,对边缘计算平台(例如,ASIC、FPGAs和嵌入系统)高效实施 DNN 的测算方案进行了广泛调查。 由于模型大小和计算数量巨大, 模型压缩是将DNN模型用于边缘设备的关键步骤。 本文侧重于权重量化, 一种硬件友好模式压缩方法, 与重量调整互补。 与对所有重量使用相同量化办法的现有方法不同, 我们建议了第一个解决方案, 将不同加权矩阵行(例如,ASIC、FGAs、FPs和嵌入系统)应用不同的测算方法。 它的动机是:(1) 不同行的权重分布不相同;(2) 模型压缩对于在边缘设备上部署DNNNNN(FGA) 模型是一个关键步骤。 为了实现这一点,我们首先提出一个硬件友好的量化的裁量机制, 用于像GA2一样的权重分配, 多重计算方法可以被替换为逻辑转换的精度的精度计。 将精度的精度匹配的精度比机制, 。 将精度配置和精度配置的精度配置的比地平地平地平地平地平地平地平地平地平地平地平地平地平调法( 。