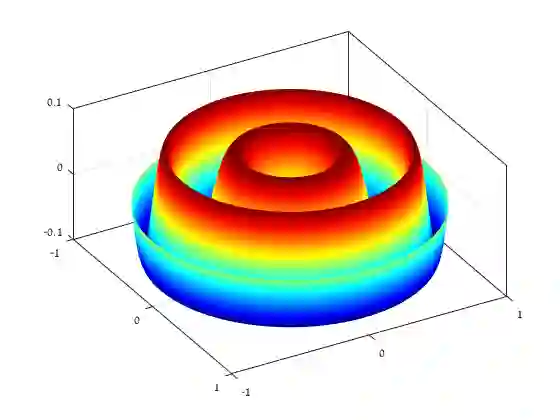
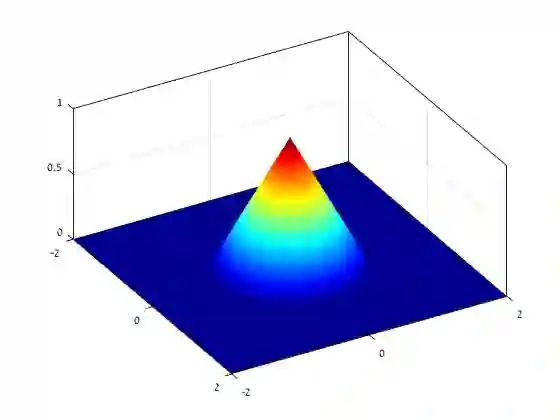
Existing depth separation results for constant-depth networks essentially show that certain radial functions in $\mathbb{R}^d$, which can be easily approximated with depth $3$ networks, cannot be approximated by depth $2$ networks, even up to constant accuracy, unless their size is exponential in $d$. However, the functions used to demonstrate this are rapidly oscillating, with a Lipschitz parameter scaling polynomially with the dimension $d$ (or equivalently, by scaling the function, the hardness result applies to $\mathcal{O}(1)$-Lipschitz functions only when the target accuracy $\epsilon$ is at most $\text{poly}(1/d)$). In this paper, we study whether such depth separations might still hold in the natural setting of $\mathcal{O}(1)$-Lipschitz radial functions, when $\epsilon$ does not scale with $d$. Perhaps surprisingly, we show that the answer is negative: In contrast to the intuition suggested by previous work, it \emph{is} possible to approximate $\mathcal{O}(1)$-Lipschitz radial functions with depth $2$, size $\text{poly}(d)$ networks, for every constant $\epsilon$. We complement it by showing that approximating such functions is also possible with depth $2$, size $\text{poly}(1/\epsilon)$ networks, for every constant $d$. Finally, we show that it is not possible to have polynomial dependence in both $d,1/\epsilon$ simultaneously. Overall, our results indicate that in order to show depth separations for expressing $\mathcal{O}(1)$-Lipschitz functions with constant accuracy -- if at all possible -- one would need fundamentally different techniques than existing ones in the literature.
翻译:恒定深度网络的现有深度分离结果基本上显示,某些以${mathbb{R ⁇ d$(如果目标精度为$\mathb{O}(1)$-Lipschitz$(如果目标精度为$\eepsilon$(美元)),那么,即使深度网络的大小以美元为指数,也不可能以恒定的准确度为基数,即使其规模以美元计算。然而,用来显示这种深度分离的功能是快速振动的,如果利普西茨的参数以美元为基数(或者通过调整功能,硬度结果适用于美元=mathalcal{O}(如果目标精度精度为$),美元=oqualth$(美元),那么我们现有的答案是否定的:与先前工作建议的直观值相比, 美元=emsil=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx) 函数显示可能的常值。