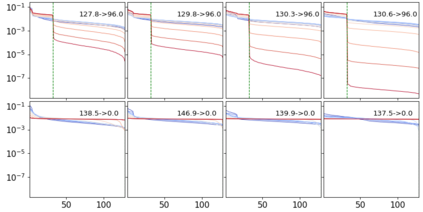
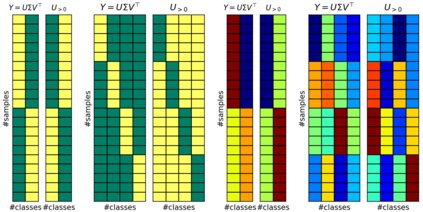
Self-Supervised Learning (SSL) surmises that inputs and pairwise positive relationships are enough to learn meaningful representations. Although SSL has recently reached a milestone: outperforming supervised methods in many modalities\dots the theoretical foundations are limited, method-specific, and fail to provide principled design guidelines to practitioners. In this paper, we propose a unifying framework under the helm of spectral manifold learning to address those limitations. Through the course of this study, we will rigorously demonstrate that VICReg, SimCLR, BarlowTwins et al. correspond to eponymous spectral methods such as Laplacian Eigenmaps, Multidimensional Scaling et al. This unification will then allow us to obtain (i) the closed-form optimal representation for each method, (ii) the closed-form optimal network parameters in the linear regime for each method, (iii) the impact of the pairwise relations used during training on each of those quantities and on downstream task performances, and most importantly, (iv) the first theoretical bridge between contrastive and non-contrastive methods towards global and local spectral embedding methods respectively, hinting at the benefits and limitations of each. For example, (i) if the pairwise relation is aligned with the downstream task, any SSL method can be employed successfully and will recover the supervised method, but in the low data regime, VICReg's invariance hyper-parameter should be high; (ii) if the pairwise relation is misaligned with the downstream task, VICReg with small invariance hyper-parameter should be preferred over SimCLR or BarlowTwins.
翻译:自强学习(SSL) 推测, 投入和双向积极关系足以学习有意义的表达方式。 虽然 SSL最近达到了一个里程碑: 在许多模式中,理论基础有限、方法具体、没有为实践者提供原则设计指南, 理论基础有限、 方法特定、 并且没有为实践者提供原则设计指南。 在本文中, 我们提议在光谱多元学习的主导下建立一个统一框架, 以解决这些局限性。 通过本研究, 我们将严格证明, ICRCReg、 SimCLR、 BarlowTwins et al. 与Laplaceian Eigenmaps、 MDextream Slay et al. 等相匹配的频谱方法相近无比。 这样, 校对将使我们能够获得( 一) 每种方法的封闭式最佳代表, (二) 每种方法的线性最佳网络参数, (三) 在培训期间使用的对每个数量和下游任务绩效的影响, 最重要的是, (四) 与全球和本地的相光谱嵌的对比和非同步方法之间的首个理论桥梁连接。 (如果Sli-liarrial sli-ration relial relide relation关系是每个的恢复方法, )