Upper and Lower Bounds on the Performance of Kernel PCA

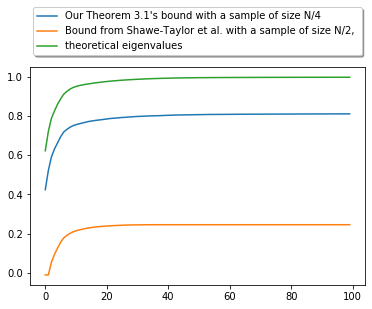
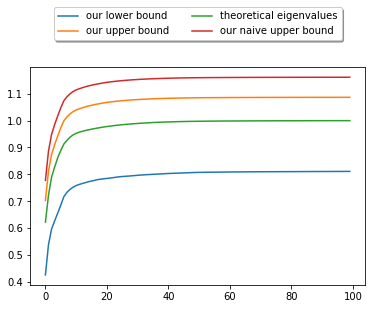
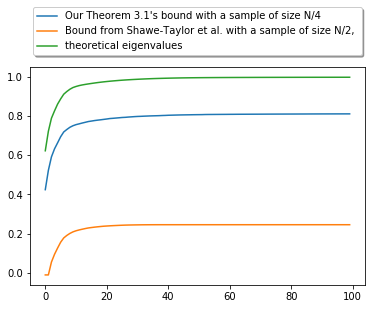
Principal Component Analysis (PCA) is a popular method for dimension reduction and has attracted an unfailing interest for decades. Recently, kernel PCA has emerged as an extension of PCA but, despite its use in practice, a sound theoretical understanding of kernel PCA is missing. In this paper, we contribute lower and upper bounds on the efficiency of kernel PCA, involving the empirical eigenvalues of the kernel Gram matrix. Two bounds are for fixed estimators, and two are for randomized estimators through the PAC-Bayes theory. We control how much information is captured by kernel PCA on average, and we dissect the bounds to highlight strengths and limitations of the kernel PCA algorithm. Therefore, we contribute to the better understanding of kernel PCA. Our bounds are briefly illustrated on a toy numerical example.