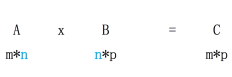干货|MIT线性代数课程精细笔记3

MIT线性代数课程精细笔记[第三课]

前言

MIT线性代数课程精细笔记[第一课]笔记见MIT线性代数课程精细笔记1。

MIT线性代数课程精细笔记[第二课]笔记见MIT线性代数课程精细笔记2。

该笔记是连载笔记，希望对大家有帮助。

1

知识概要

前面介绍了向量与矩阵之间的乘法，这一节我们要介绍两个矩阵之间的乘法。 并讨论逆矩阵存在的条件。

最后又介绍了求解逆矩阵的方法。

2

 矩阵乘法

2.1 矩阵乘法最常见的求解方式

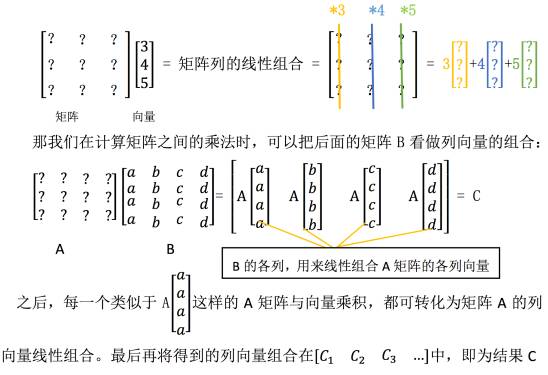
2.2 列组合与行组合方式

2.2.1 列组合

还记得我们之前学习过矩阵与列向量的乘积，得到一个列向量：

这种方法的关键就是将右侧矩阵 B 看做列向量组合，将问题转化为矩阵与向 量的乘法问题。也表明了矩阵 C 就是矩阵 A 中各列向量的线性组合，而 B 其实 是在告诉我们，要以什么样的方式组合 A 中的列向量。

2.2.2 行组合

同样，按照形式，这次将矩阵 A 看做行向量组合就行了：

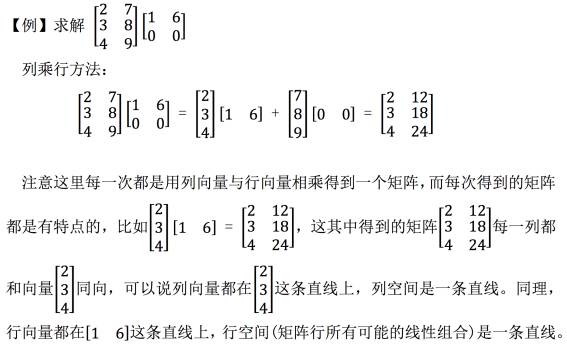
2.3 列乘以行

2.4 分块做乘法

分块乘法就是宏观上的矩阵乘法，比如现在有一个 50*50 的矩阵与 50*50 矩阵相乘，一个一个进行运算很麻烦，尤其是如果矩阵在某一区域上有一定的性质， 那么我们可以将其分块，如：

3

逆矩阵

3.1 逆矩阵介绍

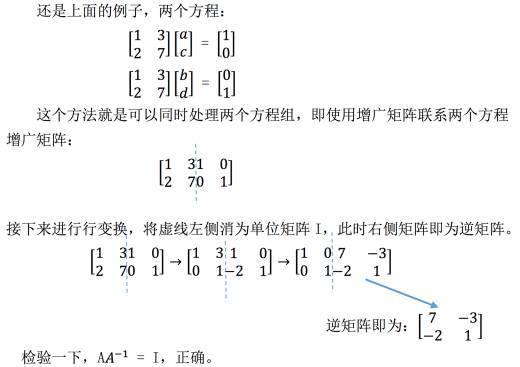
3.2 逆矩阵求解 

3.2.1 高斯-若尔当方法

接下来论证它的合理性：

4

 学习感悟

这节介绍了认识矩阵乘法的不同角度，并介绍了逆矩阵的相关知识以及如何 即求解逆矩阵。

这节内容很好的体现了我自己认为的这门课的优点之一：少有繁琐的证明，更多的理解与类比。多从向量，空间，线性组合的角度去认识矩阵之间的运算，这是这门课的核心之一。

希望对大家有帮助~

---

☞  哈尔莫斯：怎样做数学研究

☞  扎克伯格2017年哈佛大学毕业演讲

☞  线性代数在组合数学中的应用

☞  你见过真的菲利普曲线吗？

☞  支持向量机(SVM)的故事是这样子的

☞  深度神经网络中的数学，对你来说会不会太难？

☞  编程需要知道多少数学知识？

☞  陈省身——什么是几何学

☞  模式识别研究的回顾与展望

☞  曲面论

☞  曲面论（第二讲）

☞  曲面论（第三讲）

☞  自然底数e的意义是什么？

☞  如何向5岁小孩解释什么是支持向量机（SVM）？

☞  华裔天才数学家陶哲轩自述

☞  代数，分析，几何与拓扑，现代数学的三大方法论

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域。

稿件一经采用，我们将奉上稿酬。

投稿邮箱：math_alg@163.com