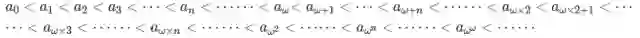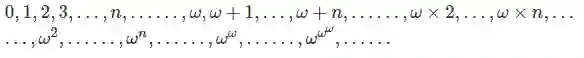0.00...1是个什么数?
某些人仍然根据有限小数的经验,认为,0.99...不等于1。他们认为,0.99...虽然是无限小数,但是有最后一位,就是在无穷远处的那一位,因此0.9循环可以写成0.99...9,显然它与1差了0.00...1,小数点后无穷个0,最后跟了个1。
这种关于无限小数的想法当然是错误的。回忆一下在实数系中引进无限循环小数的目的和依据:有理数在实数中稠密(即处处都有,任何一个小区间里都有有理数),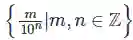
那么,0.00...1是个什么数?
首先指出,它既不是有限小数,也不是我们平常所见的无限小数,因此它根本不是一个实数。
它不是个有限小数,这是显然的,因为小数点后面有无穷个0。那它为什么不是无限小数呢?前面已经说过,任何一个无限小数,后面的小数位按从左到右的顺序与自然数一一对应,任何一个小数位都对应一个有限的自然数。反观0.0...1,最后的那个1,不对应任何有限的自然数,前面的无限多个0就已经把所有自然数都对应完了。从小数运算规律来看的话,如果要把0.0...1与0.99...相加,那么0.99...中所有的9都与0.0...1中的0对应相加,0.0...1最后的那个1要加在哪一位呢?如果按无限小数对应实数的规则把它放在实数轴上,它要放在哪里呢?它非负,又小于所有形如 1/10^n的数,这样的数只有0。因此前面的无限多个0就已经决定了它只能是0了,后面的1对它的值来讲没有意义,没有存在的必要。
虽然在实数的范围内它是没有必要存在的表达式,但我们依然有必要从形式上讨论它,因为现在的数系发展早已经超越了实数,从一维的实数扩展到高维的复数、四元数等;从标准的实数扩展到了非标准的超实数、广义实数等。所以数的范围在扩大,概念并不唯一。在其它数系中是否可能有它的身影呢?我们最好先看看这个数的特征。
因为小数点后面的0的个数已经是无限的了,这些0占满了所有以自然数为标号的小数位,然后在这些无穷多个0后面紧接着又出现了一个1,已经超出了以自然数为下标的数列的研究范围。对于这个形式上的“数”,仅有自然数的知识就不够了,需要把自然数向无穷情形做一种推广。回想上一节的无穷基数的理论,它就是从“ 个数”角度把自然数推广到了无穷的情形,但对于我们的问题,光是讨论小数位的个数是不行的,因为我们说过,在可数无穷多个元素基础上增加一个元素,元素个数没什么改变,仍然是可数无穷,你很容易把最后添加的那个1对应自然数的第一个元素,然后把原来的每个对应位都向后移动一位,所有元素仍然是一一对应于自然数集的。
但是注意到,一旦把一个小数的数位顺序打乱,它的值就变了,它必须保持原来的顺序。因此我们需要一些无穷序数的知识,它是自然数向无穷世界的另一种推广。
一般而言,序数是用来表示有序序列中位置的数,量数(或叫基数)是用来表示“有多少数量”的数。
序数对应于排列,如在以下句子中的“一”及“二”:“这人一不会打字,二不懂速记,所以不可以做秘书。”量数对应于量词,例如在以下句子中的“一”及“四”:“有一个橙,有四个柑。”
有关序数的定义,你可以查阅wiki百科“序数”词条。但那些形式化的定义对初学者来说都太抽象。我们可以先看一下序数的样子。首先需要知道“良序集”的概念:
在一个集合A上定义一个二元关系“≤”,如果满足:
①对每个x∈A,有x≤x(自反性)。②若x≤y与y≤x则x=y(反对称性)。③若x≤y,y≤z则x≤z(传递性)。④对任何x∈A,y∈A,x≤y或y≤x中必有一成立,则称"≤"为A上的全序关系,称A在“≤”关系下为全序集,简记为(A,≤)。
自然数集、实数集在数的“小于等于”关系下都是全序集,数的“小于等于”关系就是这些集合上的全序关系。对于集合{{1,2,3},{1}, {2}},包含关系“⊆”就不是全序关系,因为包含关系虽然满足上述的前三条,但在这个特殊集合上它不满足第四条,{1}和{2}就没有谁包含谁的关系。
如果一个全序集(A,≤),它的任何非空子集都有最小元素,则称≤为良序关系,A在“≤”下为良序集。自然数就是一个典型的良序集,实数集在数的大小意义下就不是良序集,不存在大于0的最小元素。
从直观上看一个良序集是什么样子呢?
首先,因为是良序,那么A中有唯一一个最小元素,记为a0,去掉a0之后还有一个最小元素,记为a1,依此类推,可得一列元素an,使得
a0≤a1≤a2≤a3≤...
因为an各不相同,所以可以按照通常的习惯把所有的"≤"改成"<"。任何不在这个序列中的元素(如果有的话)都比这列元素中的任何一个大。从A中去掉所有的an,如果还能得到一个非空子集的话,那么这个子集中还有最小元素。刚才标记an序列的时候所有的自然数都用上了,那么这个元素就赋于一个新的标号:记为aω,依此类推,又得到一列元素a(ω+n),所以现在A中的前面一部分元素在"<"的顺序下排成这个形状:
其中三点的省略号代表有限个元素,六点的省略号代表无限个元素。an和aω之间有无穷个自然数标号元,a(ω+n)和a(ω*2)之间有无穷多个(ω+自然数)标号的元素,a(ω*n)与a(ω^2)之间有无穷个标号为形如(ω*k+r)(k,r都为自然数)的元素......
这里的元素下标就是序数。序数,就是标定良序集中元素顺序的标号,是自然数的一种推广。初步的,我们得到最前面一些序数的形状:
但是,这样的描述缺乏数学上的严谨性,总不能把一个数学上的序数概念定义为“如上所示的一列数”吧?另外,上面的一列数有什么性质?是否有一个最大元?是否每一个良序集都可以用序数给每一个元素标号?这些问题都有待严格定义序数。
序数的一个直观且严谨的定义是用归纳法定义的,它完全是序数生成过程的描述:
1) 空集 Ø 是序数;
2) 如果a是序数,则a的后继 a∪{a} 也是序数;
3) 如果A是由序数构成的集合,那么A中所有元素的并集也是序数;
4) 所有的序数都由上述三条界定。
由上面的定义,我们可以写出开头的一些序数如下:
Ø,Ø∪{Ø}={Ø},{Ø}∪{{Ø}}={Ø,{Ø}},{Ø,{Ø},{Ø,{Ø}}},...
将开头的这些有限序数分别简记为1,2,3,4,...,n,它们就是自然数在集合论中的定义。由此可见,
0=Ø,1={Ø}={0},2={Ø,{Ø}}={0,1},3={Ø,{Ø},{Ø,{Ø}}}={0,1,2}...n={0,1,2,...,n-1},n+1=n∪{n}={1,2,3,...,n}。
这些自然数有一个共同的特点:都是由空集通过定义中的第二条生成的,每一个都既属于后一个,又包含于后一个。所有的自然数可以构成集合,这是公理集合论的假设。因此,根据序数的定义条款3),所有自然数的并集(记为ω)也是序数。那么所有自然数的并集是什么呢?
注意到任何一个自然数n,n是n+1的元素,因此n∈ω,反过来任意ω中的元素都属于某个自然数,而自然数的元素也是自然数,所以ω就是自然数集本身。反复应用上面的定义,就可以得到类似于上面的那一长串序数。由序数的定义,还可以有超限归纳法,并证明,对于任何一个序数集,包含关系"⊆"是一个良序关系,并且∈是⊆的严格序关系,既 a∈b等价于a⊆b且a≠b。
下面证明:任何一个良序集都可以用序数为元素按顺序标号。设X是良序集,用0标记最小元,1标记第二小的元素,...,假设无法用序数为X中所有元素标号,那么能够获得标号的元素和无法获得标号的元素分别组成X的两个子集,分别记为Y和 Z,Y中的元素都比Z中的小。若Y中有最大元,标号为a,那么为Z中最小元标号a∪{a},由定义,它也是序数,大于所有Y中的标号,矛盾;若Y中无最大元,那么Y中所有元素标号构成集合,此为序数构成的集合,所有序数之并集也是序数,这个序数未出现在Y的标号中,(因为假设它是Y某元素的标号,Y中无最大元,那么Y中总能找到比这个序数大的标号,即真包含这个序数的标号,矛盾)把Z中最小元素标记为此序数,也与假设矛盾。
至于是否有不可数无穷个序数,是否每个集合都能够定义良序关系,这里不去探讨了,可以参看公理集论的内容。
有了序数的概念,那么0.00...1的问题就有了理论依据:前面的0对应的标号都是自然数,最后的那个1对应第一个无穷序数ω。那么,我们看到,它确实跟0.99...不是一类数,暂且叫它“超级无穷小数”吧。
以下设x=0.00...1
▋第一个问题:0.00...1*10=?
根据有限小数的经验,一个小数乘以10,既可以理解为小数点向右移动一位,也可以理解为所有数位向左串一位。对于第一种理解,小数点向右移动一位,前面的0 还是无穷个,仍然可以占满所有自然数标号,因此有x*10=x。对于第二种理解,所有数位向左串一位,前面无穷个0的标号都减1,第0个标号移到了整数位,这没有问题。但最后的那个标号为ω的,却有问题:在序数中,不存在ω的前一个和ω紧临的序数,它向前移动一位,立刻跌进了深渊,消失在自然数尾部那个无穷的迷雾中了,因此可以有x*10=0.000...=0。
▋第二个问题:0.00...1/10=?
根据有限小数的经验,一个小数除以10,既可以理解为小数点向左移动一位,也可以理解为所有数位向右串一位。对于第一种理解,有x/10=x,对于第二种理解,x/10=0.00...01,注意0.00...01这个数最后的0和1分别对应ω和ω+1。
这是假定超级无限小数的数的位置是按前后顺序排成良序集,从而根据有限小数的经验推得的几种可能情况。但是可以看到,孤立地研究单独的一个数,可以有很多种可能,如果不把它放在具体的数系中,这种研究是没有什么意义的。
∑编辑 | Gemini
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域
稿件一经采用,我们将奉上稿酬。
投稿邮箱:math_alg@163.com