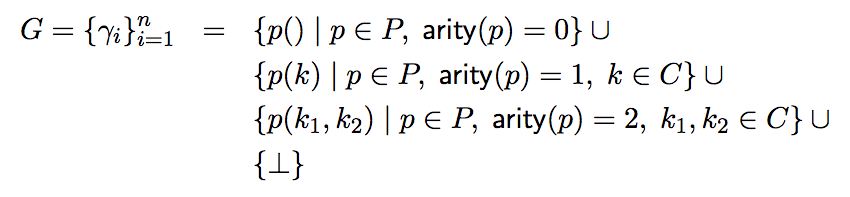DeepMind新研究：可微归纳逻辑编程，融汇神经网络与逻辑编程之长（上）

来源：DeepMind

编译：weakish

在机器学习领域中，以深度学习为代表的神经网络和以归纳逻辑编程为代表的符号程序生成似乎是两条泾渭分明的路线，各有自己的优势和劣势。而人类的认知过程，无痕地结合了两者。比如，当人踢球的时候，当球到达脚下时，人能够不假思索地辨认出这是一个球。这里的不假思索，是指人并不需要进行逻辑推理，人的神经网络自动运算出了结果。如果你问一个人，是怎么认出这是一个球的，他很难回答。然后，人通过思考（逻辑推理），将球传给合适的队友。受此启发，DeepMind的研究科学家Richard Evans和Edward Grefenstette提出了可微归纳逻辑编程∂ILP，结合了神经网络和归纳逻辑编程的优势。

当然，∂ILP也不是完美无缺，目前，∂ILP需要大量内存才能发挥威力。

逻辑编程

首先让我们温习一下逻辑编程的基本概念。

在逻辑编程这一范式中，构成程序的关键成分既不是命令（命令式编程），也不是函数（函数式编程），而是“如果……那么……”（if-then）规则（rule），这些规则称为子句（clause）。

确定性子句是符合以下形式的规则：

a <- a₁, ..., a_m

其中，a称为头原子head atom，a1, ..., am （m>=0）称为体原子body atom。这一规则从右往左进行解读：如果右边的所有原子（体原子）均为真，那么左边的原子（头原子）为真。

原子（atom）是一个元组p(t₁, ..., t_n)，其中，p是一个n元谓词（n-ary predicate），t₁, ..., t_n为项（term），项可能是变量（variable），也可能是常量（constant）。不含变量的原子称为基础原子（ground atom）。

在一阶逻辑（first-order logic）中，项还可能是函数符号（function symbol）。例如，假设c为常量，f为单元函数（one place function），那么f(c)、f(f(c))、f(f(f(c)))，……均为项。在Datalog之类的系统中，子句有一个限制，只允许变量或常量作为项，不允许函数符号作为项。研究人员也采用了这一限制（我们很快将解释如此限制的原因）。

将规则中的所有变量替换为常量后，得到基础规则（ground rule）。例如，应用θ = {a/X, b/Y}（大写字母表示变量，小写字母表示常量）到子句

connected(X, Y) <- edge(X, Y)

得到基础规则：

connected(a, b) <- edge(a, b)

完全由基础原子的集合定义的谓词称为外延谓词（extensional predicate），由子句的集合定义的谓词称为内涵谓词（intensional predicate）。

给定子句集合R和基础原子r，如果所有满足R的模型同时满足r，那么R蕴涵（entail）r，记为R ⊨ r。

判定R是否蕴涵r，有两种思路。第一种是演绎式的，从R出发，演绎出所有可能的子句con(R)（不断应用R中的规则，直到无法得出新的结论），然后查看下r是否在其中r ∈con(R)。第二种是归纳式的，从r出发，在R中寻找所有替换变量为常量后头原子为r（a[θ ] = r）的规则，然后证明相应的体原子（a₁[θ], ..., a_m[θ]）为真。第一种演绎式的思路称为正向链（forward chaining），第二种归纳式的思路称为反向链（backward chaining）。

前面我们提到，研究人员限定了子句为确定性Datalog子句，这样语言是可判定的（decidable），并且正向链推理（forward chaining inference）总能终止。

归纳逻辑编程

归纳逻辑编程（Inductive Logic Programming，ILP）的灵感来源于归纳推理。在归纳推理中，基于一定的背景知识，我们从一些正面的例子和反面的例子中归纳出一些规则。同样，归纳逻辑编程基于一定的背景知识，根据一些正面的例子和反面的例子，生成相应的程序。

用形式化的语言来说，ILP问题是由基础原子组成的元组(B, P, N)，其中：

• B为背景知识

• P为正例，即从目标谓词将要学习的外延之中选取的例子

• N为反例，即从目标谓词将要学习的外延之外选取的例子

然后，给定一个ILP问题(B, P, N)，它的一个解答（solution）是满足以下条件的确定性子句的集合R：

• 对所有r∈P， B, R ⊨ r

• 对所有r∈N， B, R ⊭ r

归纳逻辑推理即为寻求ILP问题的解答的过程。

作为可满足性问题的ILP

大体而言，ILP可以分为两类：

1. 自底向上（bottom-up） 首先检查例子的特征，从例子中提取特定的子句，然后概括这些特定子句。例如Muggleton等1995年提出的Progol。

2. 自顶向下（top-down） 根据语言定义生成子句，然后在正例和反例上测试生成的程序。例如TopLog、TAL、Metagol。

研究人员采用的即为自顶向下的方法，基于语言模板（langugae template）生成程序，然后在正例和反例上测试生成的程序。

程序模板

回顾一下，ILP问题可以用元组(B, P, N)表示。那么，自顶向下的ILP问题就可以用元组(L, B, P, N)表示，其中，新增的L表示语言框架（language frame）。

那么，语言框架该如何表示呢？

从直觉上而言，语言框架勾勒出了程序的大致形状。想想逻辑编程程序大概会是一个什么形状？

很容易想到，逻辑编程程序中会有常量（不妨用C表示常量的集合），也会有变量（不妨用V表示变量的集合），然后是一些包含常量和变量的谓词（不妨用P表示）。那么，逻辑编程程序大概是这样的：

L = (P, V, C)

这个框架很有概括性，但是我们的语言框架最终是要用来生成程序的，从这一角度而言，这个框架太概括了，以至于搜索空间几乎是无边无际。那么，我们需要做一些限定。

首先，我们将P（谓词集合）分为两部分，一部分是要生成的目标谓词（target）另一部分是已知的谓词，在已知的谓词中，我们用常量替换变量，这样可以得到外延谓词的集合（P_e）。

其次，为了缩小搜索空间，我们需要限定谓词的元数（arity）。

这样，我们就得到了新的语言框架：

L = (target, P_e, arity_e, C)

语言框架大致勾勒出了程序的性质，但要生成程序，我们还需要一些生成的设定（超参数）。

首先，正向链推理不能无限进行下去，我们需要限定正向链推理的最大步数（用T表示）。

其次，我们需要基于一组规则模板（rule template）生成子句，再将这些子句拼成内涵谓词（用rules表示）。

最后，我们需要一些辅助的（内涵）谓词，帮助定义目标谓词（用P_a）表示。同样，这些辅助谓词的元数需要限制（用arity_a）。

这样，我们就得到了程序模板（program template）：

(P_a, arity_a, rules, T)

如前所述，rules是内涵谓词到一组规则模板的映射。那么，具体的规则模板是如何定义的呢？

首先，研究人员用一个整数（int）标记了子句中的原子可以使用内涵谓词（int=1），还是只能使用外延谓词（int=0）。

其次，研究人员限定了子句中的变量数目（避免过于复杂的子句）。

这样，最终的规则模板定义为(v, int)。同样，这些限制是为了收紧搜索空间。

前面提到一组规则模板，实际上，一组规则模板可以限定为一对（pair）规则模板。这一限定不会影响谓词的概括性。类似lambda演算通过柯里化（currying）将多元函数改写为单元函数，我们同样可以将由超过两个子句组成的谓词改写为由两个子句组长的谓词。

例如，假设谓词p由三个子句p(X, Y) <- β₁、p(X, Y) <- β₂及p(X, Y) <- β₃定义，那么，通过创建一个辅助谓词q，我们可以改写上面的定义为：

1. p(X, Y) <- β₁

2. p(X, Y) <- q(X, Y)

3. q(X, Y) <- β₂

4. q(X, Y) <- β₃

将程序模板代入语言框架，我们得到语言（language） (P_e, P_i, arity, C)，其中

• P_i = P_a ∪ {target}

• arity = arity_e ∪ arity_a

语言决定了所有基础原子的集合G。为了收紧搜索空间，研究人员限制了谓词元数的范围（不超过2），因此：

其中，最后的⊥表示伪原子（falsum atom），值永远为假。

生成子句

给定规则模板τ，我们可以生成满足该模板的子句集合cl(τ)。为了缩小搜索空间，我们需要一些限制。

前一小节已经提到了一些限制：

1. 谓词的元数不超过2

2. 谓词由2个子句组成

如前所述，这些限制没有损害程序的概括性（或者说表达能力）。

同时，研究人员限定了目标谓词仅由涉及自由变量的原子组成，不允许包含任何常量。这一限制非常重要，由于不允许包含常量，生成的目标谓词注定是概括性的，避免了过拟合的问题。

此外，研究人员还剔除了一些生成子句：

1. 不安全子句（头子句中使用了体子句中未出现的变量）

2. 循环子句（体子句包含头子句）

3. 重复子句（排列组合体子句中的原子后，和另一子句等价）

4. 不遵循内涵标记int的子句（例如，尽管int标记设为0，仍然包含内涵谓词）

可满足性

给定程序模板Π，内涵预测p的第i（i∈{1, 2}）个规则模板记为τ_pⁱ，由τ_pⁱ生成的子句集合记为cl(τ_pⁱ)，其中第j个子句记为C_p^{i, j}。表明C_p^{i, j}中程序实际使用的子句的布尔值变量（即零元预测构成的原子）的集合记为Φ。

由此，推理问题可化归为可满足性问题。我们可以使用一个可满足性求解器（SAT solver）搜寻Φ的真值赋值（truth-assignment），然后据此提取相应的生成规则。

研究人员精心设计了可满足性求解器，确保它的权重训练是可微的。具体架构我们将在下篇介绍，现在，先让我们看看∂ILP的效果吧。

∂ILP在标准ILP问题上的表现

研究人员在三类任务上试验了∂ILP：

1. 标准的ILP问题（基于离散、无误的输入）

2. 错误标注的问题

3. 模糊问题

本文将介绍∂ILP在标准ILP问题上的表现。后两类问题将在下篇介绍。

自然数上的Even/1问题

首先，让我们来看一个自然数上的even（偶数）谓词问题（even/1表示这是一个一元谓词）。

背景知识包含基本的算术，如zero谓词和10以内的succ关系：

B = {zero(0), succ(0,1), succ(1,2), succ(2,3), ..., succ(9, 10)}

正例：

P = {target(0), target(2), target(4), target(6), target(8), target(10)}

反例：

N = {target(1), target(3), target(5), target(7), target(9)}

研究人员将even谓词应用于10以上的数字，作为验证和测试。

可能的语言模板之一：

• P_e: {zero/1, succ/2}

• P_i: {target/1, pred/2}

其中，pred是一个辅助二元谓词，常量C为{0, 1, ..., 10}。

可能的程序模板之一：

τ_target,1 = (h = target, n_∃ = 0, int = 0) τ_target,1 = (h = target, n_∃ = 1, int = 1) τ_pred,1 = (h = pred, n_∃ = 1, int = 0) τ_pred,2 = null

∂ILP可以可靠地完成这一任务。找到的其中一个解答为：

target(X)  <- zero(X)
target(X)  <- target(Y), pred(Y,X)
pred(X, Y) <- succ(X,Z), succ(Z,Y)

注意，这个解答很简单，但并不简单，其中包括递归。

Even/Odd

even（偶数）的另一种定义是与odd（奇数）同时定义。

背景知识、正例、反例同上，∂ILP找到的一个解答为：

target(X)  <- zero(X)
target(X)  <- pred1(Y), succ(Y,X)
pred1(X, Y) <- target(X,Z), succ(Z,Y)

注意，target和pred1互递归（mutually recursive）。

图是否有环

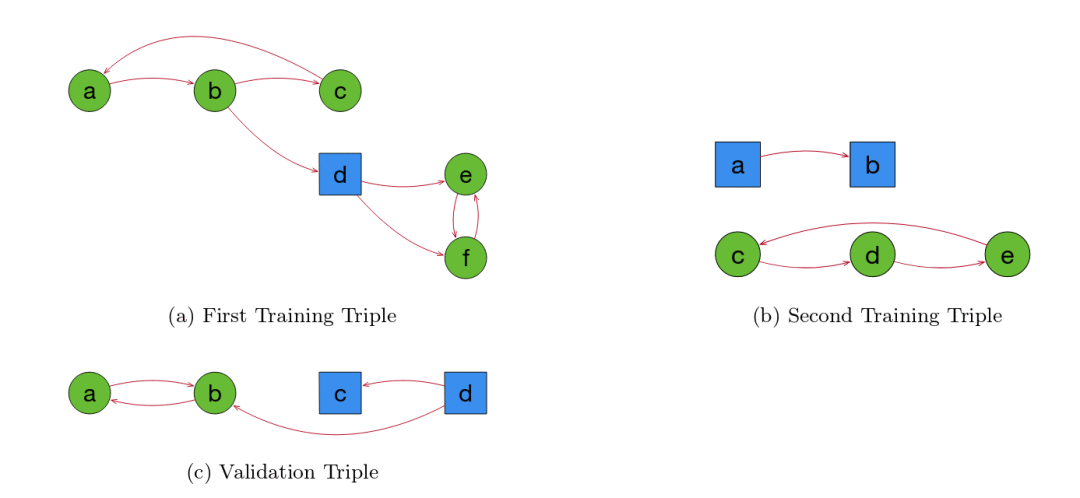
这一任务学习is-cyclic（是否有环）谓词。

上图中，a和b为训练数据，c为验证数据。其中，a和b对应的(B, P, N)并不相同。如前所述，这有助于系统正确地概括。

该任务的语言为：

• Pe = {edge/2}

• Pi = {target/1, pred/2}

• C = {a, b, c, d, e, f}

∂ILP找到的其中一个解答为：

target(X) <- pred(X,X)
pred(X, Y) <- edge(X,Y)
pred(X, Y) <- pred(X,Z), pred(Z,Y)

注意，该任务属于一阶逻辑无法解答的问题。

Fizz-Buzz

Fizz-Buzz程序源于儿童游戏，在这个游戏中，玩家从头开始数数（自然数），但数到3的倍数时说“Fizz”，数到5的倍数时说“Bazz”。令人吃惊的是，大部分计算机科学的毕业生无法在几分钟内写好Fizz-Buzz程序。在这篇论文之前，也没有神经程序推理系统能够学习Fizz-Buzz问题。

研究人员将Fizz-Buzz问题转化为了一个课程学习（curriculum learning）任务，首先让∂ILP学习Fizz，当∂ILP学习到正确的规则后，将这些规则作为公理，传递给学习Buzz的任务。

学习Fizz问题的语言为：

• P_e = {zero/1, succ/2}

• P_i = {target/1, pred1/2, pred2/2}

• C = {0, 1, 2, 3, 4, 5, 6}

背景公理为：

{zero(0)} ∪ {succ(n,n+1) | n ∈ {0, ..., 5}}

正例和反例为：

P = {target(0), target(3), target(6)}
N = {target(1), target(2), target(4), target(5)}

∂ILP学习到的其中一个解答为：

target(X) <- zero(X)
target(X) <- target(Y), pred1(Y,X)
pred1(X,Y) <- succ(X,Z), pred2(Z,Y)
pred2(X,Y) <- succ(X,Z), succ(Z,Y)

研究人员将∂ILP学习到的规则pred1和pred2编译为背景公理：

pred1(n,n+3)
pred2(n,n+2)

学习Bazz问题的语言为：

• Pe = {zero/1, succ/2, pred1/2, pred2/2}

• Pi = {pred3/2, target/1}

• C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

背景知识∂ILP为：

{zero(0)} ∪ {succ(n,n+1) ∪ {pred1(n,n+3)} ∪ pred2(n,n+2) 

注意，语言和背景知识中使用了从Fizz问题中学到的规则。

正例、反例为：

P = {target(0), target(5)}
N = {target(1), target(2), target(3), target(4), target(6), target(7), target(8), target(9)}

∂ILP有时（30%权重初始化）能找到这一问题的正解，找到的其中一个解答为：

target(X) <- zero(X)
target(X) <- target(Y), pred3(Y,X)
pred3(X,Y) <- pred1(X,Z), pred2(Z,Y)

这个例子很好地体现了∂ILP的很多优势：

1. 只需很少的数据（正例和反例）就能找到正解

2. Fizz问题中，训练的数据只包括6以下的数字，Bazz问题中，训练的数据只包括9以下的数字，而∂ILP能生成高度概括的程序，毫无压力地处理训练中未见的数字

3. ∂ILP从一个任务中学到的知识，能够以压缩和可读的形式直接迁移到新任务。

基准测试

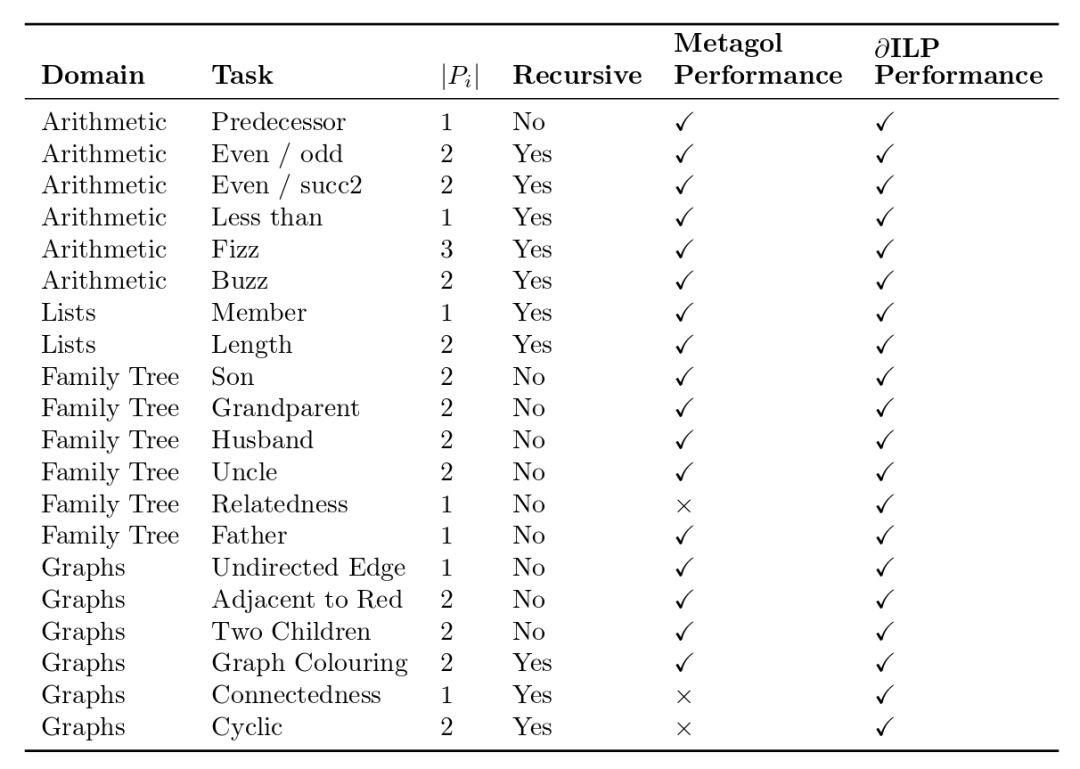
研究人员总共在20个标准ILP任务上测试了∂ILP的表现，并与当前最先进的ILP模型metagol进行了对比。

从上表我们可以看到，∂ILP能够完成所有20个任务，而metagol未能完成其中3个任务（未完成的定义为超时，∂ILP和metagol的时间限制均为24小时，运行环境为工作站）。

当然，由于∂ILP需要大量的内存，研究人员将谓词元数限制在2以下，因此metagol可以完成的一些需要三元谓词才能解决的任务，∂ILP目前尚不能完成。

未完待续

在这篇文章中，我们介绍了如何将归纳推理问题转化为可满足性问题，以及∂ILP在标准ILP任务上的表现。下篇我们将介绍求解可满足性问题的可微架构，以及∂ILP对错误标注数据的鲁棒性，以及如何应用∂ILP到非符号数据。除此以外，我们还将讨论∂ILP的劣势和可供改进之处，并和其他一些基于神经网络生成程序的工作进行比较。敬请期待。