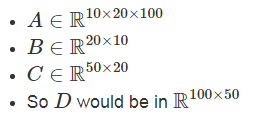能「看到」的张量运算：因子图可视化

选自GitHub

作者： Rajat Vadiraj Dwaraknath

参与： Panda

张量运算有时候并不容易直观地理解： 为什么有时候改变计算顺序不会影响结果，同时又能极大节省计算成本？ 使用因子图来可视化或许能为人们提供简洁直观的理解方式。 Rajat Vadiraj Dwaraknath 近日发布了一篇文章，介绍了他在使用因子图可视化张量运算方面的心得。

从格罗滕迪克那里，我学习到不要以证明过程的难度为荣：困难意味着我们尚未理解。也就是说我们要能绘制出让证明过程显而易见的图景。 ——著名数学家 Pierre Deligne

当维度超过 2 或 3 时，理解涉及多维数组的运算就会变得相当困难。但是，矩阵本身的特定性质可能让你在初次与它们相遇时深感惊讶。轨迹运算的循环性质就是其中一例。

我最近遇到个能可视化这些所谓的张量运算的好工具——因子图（factor graphs），它能得到视觉上很明显（如循环轨迹）的结果。 尽管我最初是在图模型和消息传递的语境中遇到因子图的，但我很快就意识到它们体现了一种更通用和更简单的概念。 在这篇文章中，我将主要在高层面介绍因子图，而不会涉及图模型或消息传递等算法的具体细节。

 

在深入因子图之前，我们先简单快速地介绍一下爱因斯坦求和符号。

 

爱因斯坦求和符号

 

爱因斯坦符号存在多种形式，尤其是在物理学领域，但我们要介绍的那种非常简单，没有任何物理学背景也能轻松掌握。

 

在矩阵乘法的定义中，

求和符号实际上是多余的。 我们可以直接舍弃它，并推断出索引 k 必须被求和，因为它没有出现在左侧。

为什么要这么做？ 好吧，我们来看一个有一般张量的案例（将其看作是超过 2 维的 numpy 数组即可）：

然后假设张量的形状如下：

其中交织着复杂的「和」与「积」，而不断写求和符号是非常烦人的。 同样，我们不需要写这些求和符号，因为我们可以通过查看仅出现在右侧的索引来暗示所要求和的索引。 用爱因斯坦表示法，写起来就简单多了：

但相比于公式 (4)，这种表示方式确实丢失了一些信息——计算求和的顺序。 现在，求和的顺序实际上不影响最终结果（福比尼定理），但事实表明某些顺序的求和过程比另一些顺序更高效（后面还会提到）。 另外，你可以使用 numpy.einsum 在 Python 中轻松尝试这些。 这篇文章更详细地介绍了 einsum，并给出了一些很好的示例： http://ajcr.net/Basic-guide-to-einsum/

 

因子图

 

带有多个不同大小的张量的和-积表达式也被称为张量网络。 除了听起来炫酷之外，这个名字也是合理的，因为你写的任何有效的爱因斯坦求和实际上都可映射为一个张量图。 （「有效」是指同样索引的不同张量的维度大小必须相等。 ）

 

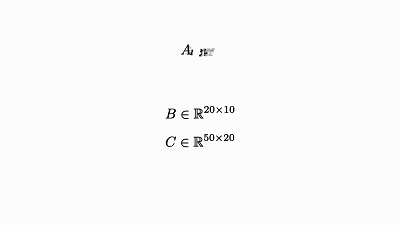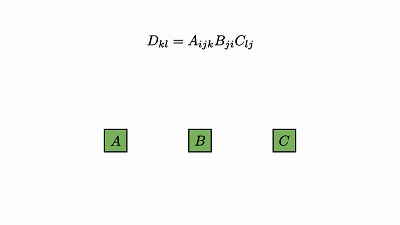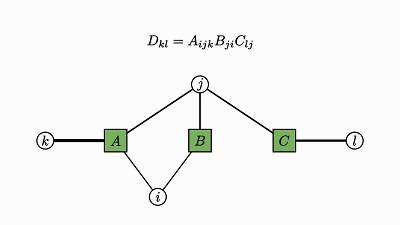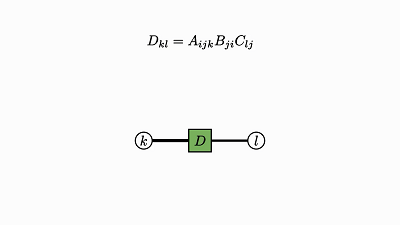
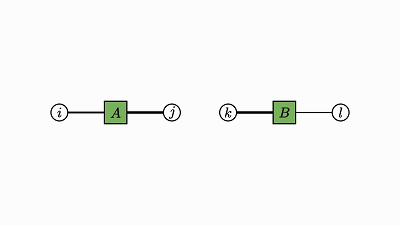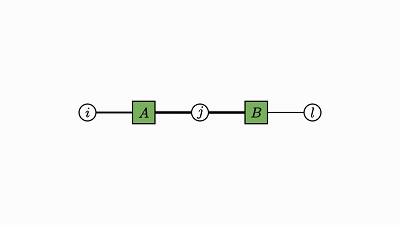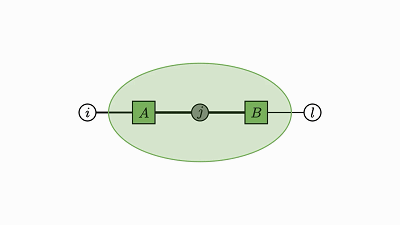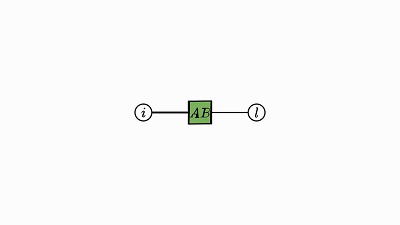
我们可以很轻松地构建出这样的图。 我们回头看看这个例子，了解下发生了什么：

• 这个图有两种节点——因子和变量

• 我们将用方框表示因子，用圆圈表示变量

• 因子对应张量 (A,B,C)

• 变量对应索引 (i,j,k)

• 边仅出现在方框和圆圈之间

•  边的规则很简单——每个因子都连接其每个索引。在上面的例子中，A_{ijk} 表示 A 连接着 i、j、k

• 边的厚度对应于因子中轴（即数组分量的长度）的大小

• 这使得图成为了方框和圆圈之间的二部图（bipartite graph）

• 仅出现在等式右侧的索引（i 和 j）会被隐式地求和。我们通过加黑图中对应的变量节点来表示它。

上面动画的最后一部分给出了一个重要的直觉观察：

 

每个因子图都有一个完全收缩的状态——爱因斯坦求和的右侧（示例中的 2 维张量 D）。 通过将图中的所有因子组合成单个因子，然后将每个灰色的变量求和，可以得到这个状态。 现在剩下的是仅连接到未求和变量的单个因子——这就是收缩状态。 示例中转变为因子 D 的绿色云很好地展示了这种收缩。

 

在我们继续探索这个奇特工具的能力之前，我们先谈谈它的来源。

 

名字从何而来？

 

这种图被称为因子图的一大原因是右侧看起来像是对左侧张量的因子分解。 在离散随机变量的概率分布语境中，这会更加具体。 如果张量为正且总和为 1，则它们可以表示在不同随机变量上的联合分布（这也是索引对应于变量的原因）。 在这种设置中，因子图是将许多变量的大型联合分解成更小的互相独立的变量集的联合。

 

因子图不仅会在概率图模型中出现，而且也会现身于物理学当中，这时候它被称为张量网络或矩阵积状态（matrix product states）。 但是，这里不会介绍这些应用的细节。

 

有一点需要注意，因子分解所需的内存实际上比整个联合要少得多（存储一个 10×10×10 张量对比存储三个 10 维张量）。

可视化的 numpy 运算

 

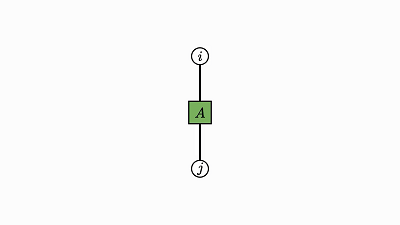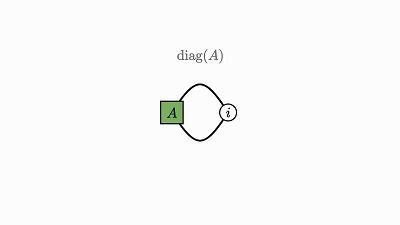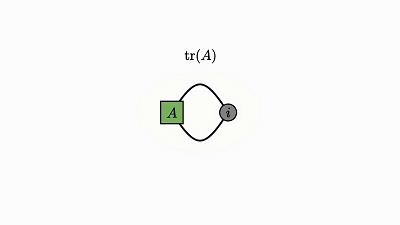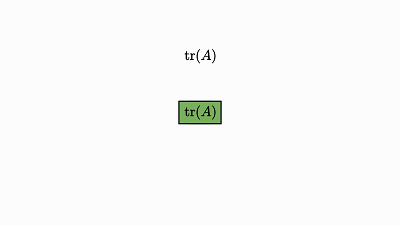
为什么这种表示方式有用？ 因为这能让我们将复杂的因子分解转换成更可视化的表示，从而更加轻松地处理。 numpy 中的数值张量运算可以很好地适用于这个框架。 下面给出了几个无需过多解释的示例：

 

矩阵-向量乘法

 

矩阵-矩阵乘法

 

逐元素求积

 

外积

 

轨迹

 

注意，没有边的因子是 0 维张量，其实就是单个数值（轨迹就该是这样）。

可视化证明

 

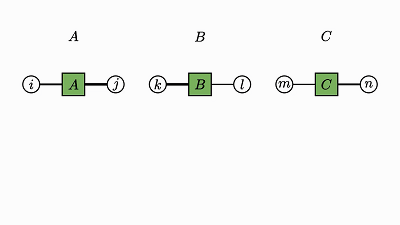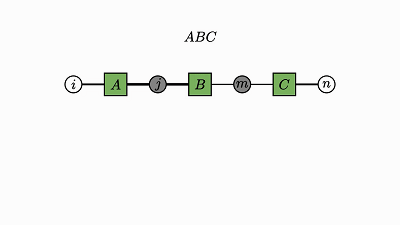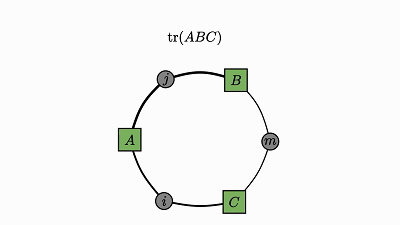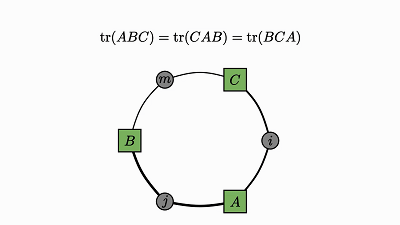
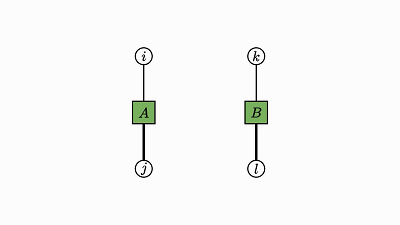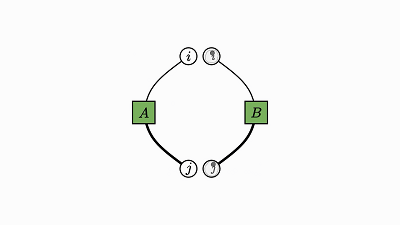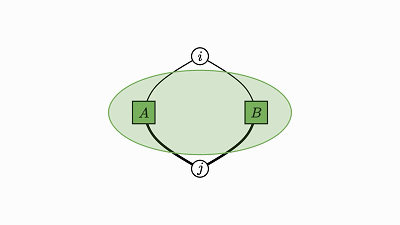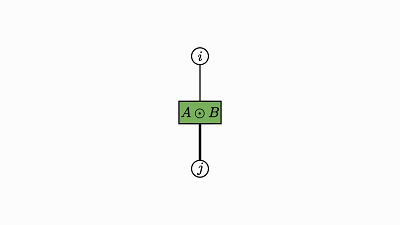
使用简洁的可视化证明，我们不仅可以理解 numpy 运算，还能迅速搞定数学定理。 下面就简洁地证明了我一开始提到的轨迹恒等：

 

轨迹是循环的

 

张量收缩的计算成本

 

现在，我们已经将因子图中的那些绿色云压缩成了一个大因子，而没有探讨这种变换究竟是怎样计算的。 将许多因子组合成单个因子并求灰色变量的和的过程涉及到两个基本的计算操作：

• 求和：移除仅有一条边的灰色节点

• 求积：将两个因子合并成一个因子

可以很容易看到，这样的操作能保留网络最终的收缩状态，所以如果我们不断应用它们直到只剩仅连接到未求和变量的单个因子，那么我们就实现了网络收缩。

 

求和

 

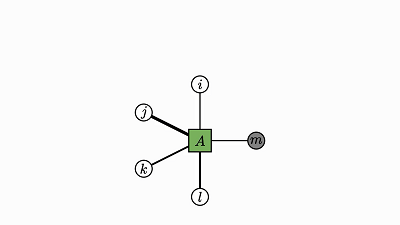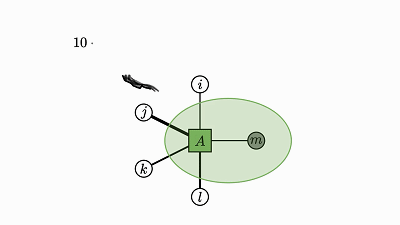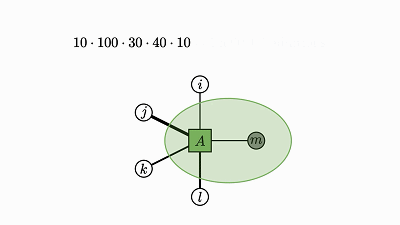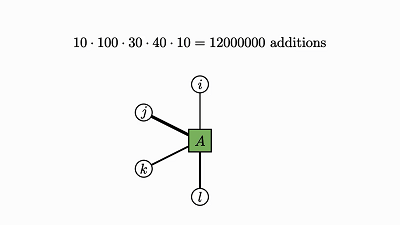
求和是不言自明的。 基本上就是将 numpy.sum 运算应用于对应的轴。 这涉及到对大小等于所有其它轴大小的积的张量求和，而且这些张量的数量就是被求和的轴的大小。 因此，加法的总数量就是所有轴大小的积。 我们也能从可视化表示中看出这一点：

求积

 

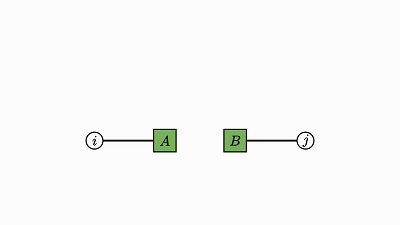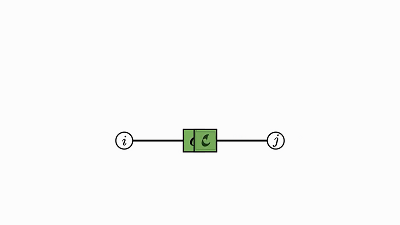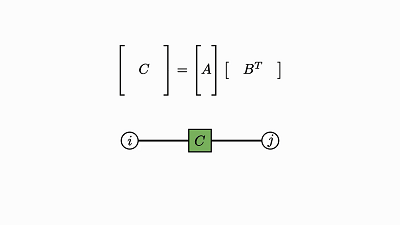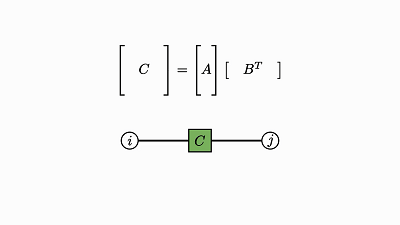
求积运算本质上就是两个张量的外积泛化为一般张量。 用爱因斯坦表示法，组合两个因子就等同于通过两个因子的项相乘而将两个因子当成一个，从而得到一个更大的因子：

这种求积是用一个因子中的每个元素与另一个因子的整体相乘。 因此最终结果的大小是各个因子的总大小的积，这会大很多。 最终积的每个元素都只是两个数值相乘的结果，所以乘法总数量就是最终积的项总数。 这也很容易可视化：

 

另外，如果两个因子共享一个变量，则两条边会结合成单条边——在效果上是执行类似于轨迹动画中的对角运算。

 

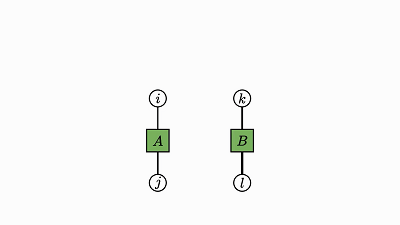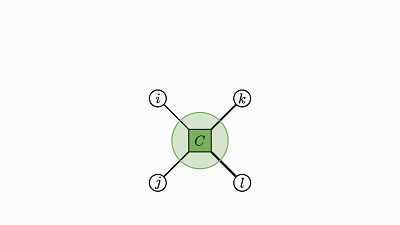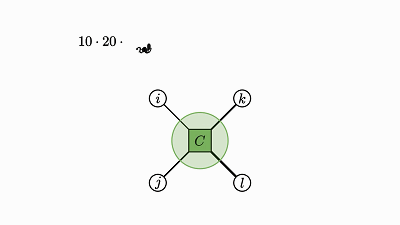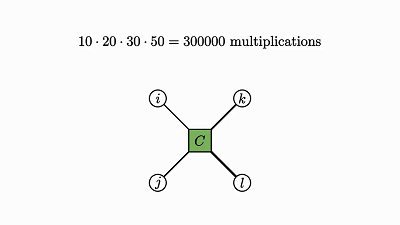
当收缩一个网络时，对变量求和并以不同的顺序组合因子会导致不同的计算成本。 研究表明，寻找实现成本最小化的收缩一般因子图的最优顺序实际上是 NP-hard 问题。 作为一个有趣的练习，你可以试试解读矩阵链乘法（matrix chain multiplication）过程，并使用因子图理解寻找一个链矩阵积的总计算成本是如何受乘法顺序影响的。 这个特定案例有非常简洁的动态编程算法，可在平方时间内获得最优顺序。

 

希望我现在已经使你信服因子图是非常强大的可视化工具。 我们不仅能用它证明一些简单的恒等关系，而且还能进一步将其用于理解一些复杂概念，比如用于概率图模型推理的有效方法。

一些细节

 

因子图其实不能精确地表示爱因斯坦求和。 你们可能已经注意到我们丢失了张量的哪个轴对应于图中哪条边的信息。 但是，只要将源自每个因子的边加上轴标签，就能轻松解决这个问题。 但这会使可视化无必要地杂乱和丑陋，所以我决定不包含它们。

 

另外，我们还可将这种可视化扩展用于不只是求和变量节点的网络。 将一个变量节点变为灰色在效果上就是将对应的轴约简为单个数值，因此我们可以用任何执行这种约简的运算替代求和。 举个例子，我们不用求和，而是取该轴中所有元素的最大值，或者就简单地索引该轴上一个特定位置。 这在 MAP 估计和最大积信念传播方面是相关的。 我们甚至可以将这种解读方式扩展到连续域，并用积分替代求和，其中的因子也不再是离散矩阵，而是连续域上的多变量函数。

机器之心「SOTA模型」：22大领域、127个任务，机器学习 SOTA 研究一网打尽。