文本挖掘从小白到精通（十三）--- 文本挖掘中会涉及的若干降维方法

2020 年 8 月 2 日 AINLP

写在前面：本文是笔者近期带的一位实习生写的第二篇实操笔记，特分享给大家，enjoy~

特别推荐|【文本挖掘系列教程】：

在文本挖掘的过程中，大家通常会采用向量空间模型来描述文本向量,但如果直接用分词算法和TF/TF-IDF方法得到的特征项来表示文本向量中的各个维,那么这个向量的维度将是非常的大。

致命的是，这种未经处理的文本矢量不仅给后续工作带来巨大的计算开销,使整个处理过程的效率非常低下,而且会损害分类、聚类算法的精确性,从而使所得到的结果很难令人满意。

尽管有word2vec、glove这样的词嵌入模型以及近段时间出现的bert、gpt2这样的高级神经网络语言模型的出现，但在文本特征结合其他类型数据（比如文本长度、情感词数量这样的数值型特征，性别、年龄段等类别特征，以及图片颜色、轮廓等图像类特征）的场景下它们也只能束手无策。

所以，在文本挖掘的任务中，降维有时候是非常关键的一环。

接下来，笔者会聊聊降维在文本挖掘中的使用问题，而且会附上相应的code，enjoy~

1 了解降维

1.1 什么是降维

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。

1.2 为什么要进行降维处理？

其实需要降维的理由很多，主要是以下几个方面：

在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率
通过降维,可以减少冗余信息所造成的误差,提高识别（或其他应用）的精度
将计算资源花费在最有价值的特征上，减少不必要的算力消耗
过高的维度会导致样本在高维变得稀疏（维度灾难），因为在高维空间中，使用欧几里得计算点之间的距离没有意义，因为算出来的都会趋同于同一个值（而很多算法都基于点之间的距离）
通过降维算法来寻找数据内部的本质结构特征

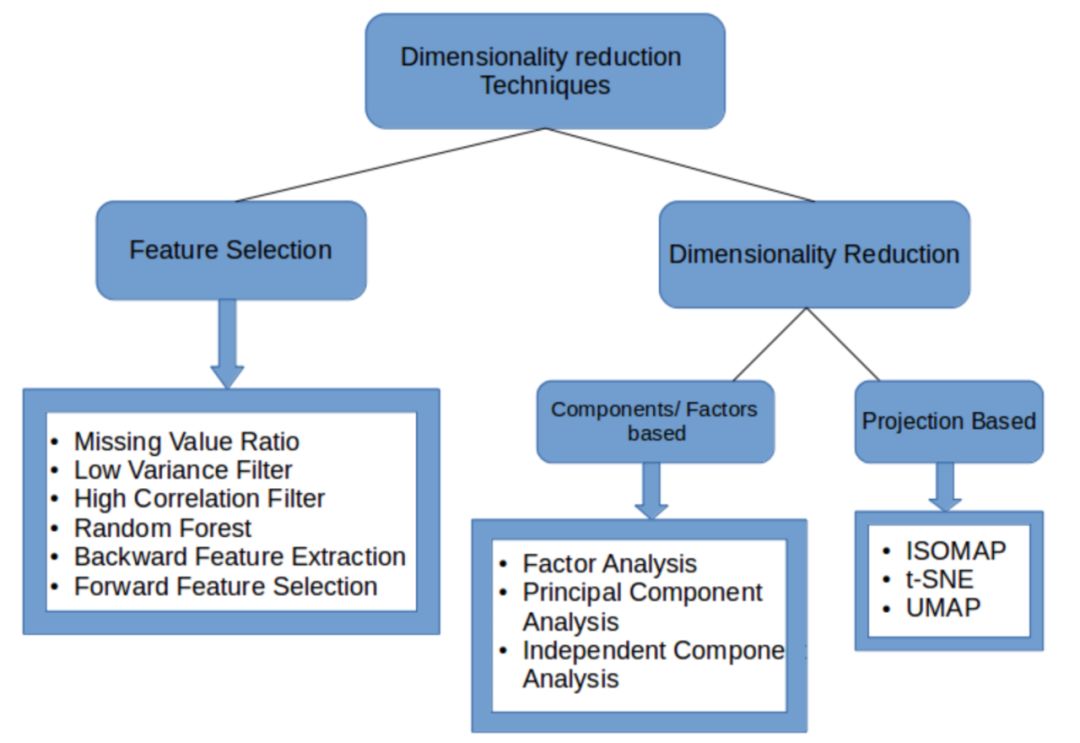
1.3 降维的实现方式

总体来看降维方式分为：

特征选择（在原特征中选择和数据集表达的信息最相关的）
直接降维（寻找一组新的较少的新变量来代表现在的变量）。

针对上述提及的2类方式，下面来谈谈具体如何实现，并配有相应的代码~

2 使用特征选择方法进行降维

2.1 从特征选择（即从原始特征中来选择）可以考虑的点

（1）缺失值过多

如果缺失值过多，那么可以考虑删除这个特征。在实际中，可以考虑设置一个阈值。当缺失比例大于这个阈值，则舍弃这个特征。

（2）低方差

低方差变量携带的信息量也很少（比如：对于一个特征，大多数样本这个特征的值都一样的，那么方差就小了。），所以可以把它直接删除。放到实践中，就是先计算所有变量的方差大小，然后删去其中最小的几个。也可以同样的使用设置阈值的方法。

（3）高相关性

对于独立的数值变量，两两计算相关性，如果相关系数超过某个阈值，就删除其中一个变量。（但要保留那些与目标变量有高相关性的变量。）通常情况下，如果一对变量之间的相关性大于0.5-0.6，那就应该考虑是否要删除一列了。

（4）随机森林

随机森林是一种广泛使用的特征选择算法，它会自动计算各个特征的重要性，所以无需单独编程。这有助于我们选择较小的特征子集。如果你用的是sklearn，可以直接使用SelectFromModel，它根据权重的重要性选择特征。

（5）其它

针对变量少的数据集（强调变量少，是因为以下这2种方式跑起来特别费资源和时间。），可以尝试：前向特征选择和反向特征消除。

反向特征消除
首先使用数据集的所有（比如：n个）特征来训练模型，评估这个模型的表现。然后分别每次去除一个特征（进行n次，因为总共n个特征），即每次使用剩下的n-1个特征来训练模型。找到去除了哪个特征之后，模型效果改变最小的那个特征，该特征可被删除。重复这个过程，直到没有特征可以被删除了。（在sklearn中可直接使用RFE。）
前向特征选择
和反向特征消除思路相反。开始只选择一个特征，假设一共有n个特征，那么就训练模型n次（因为总共n个特征，每次只使用1个特征。）给出最好表现的特征成为起始使用的特征。重复这个步骤，每次增加一个特征（每轮选出一个使得模型表现有最大提升的）。直到模型表现没有明显提高为止。（sklearn中，可使用f_regression.）

2.2 特征选择的示例

这里使用人人都是产品经理上若干文章的互动数据（点评赞阅、收藏等），它们是数值型的数据。

2.2.1 数据导入及数据清洗

import pandas as pddf = pd.read_excel('/home/kesci/input/cluster_dataset8319/7-11-2000.xlsx')df = df.drop_duplicates()  #对数据集进行去重处理  def change_to_unified_unit(df, col_name):  #将带万/M单位的数据修改为纯数值数据          rows_needed_change_unit = df[col_name].str.contains('万')   for i,row in df[rows_needed_change_unit].iterrows():              df.at[i,col_name] = '{}'.format( (float(row[col_name].split('万')[0])) *10000)          rows_needed_change_unit = df[col_name].str.contains('m')
   for i,row in df[rows_needed_change_unit].iterrows():               df.at[i,col_name] = '{}'.format( (float(row[col_name].split('m')[0])) *1000000)                   rows_needed_change_unit = df[col_name].str.contains('M')          for i,row in df[rows_needed_change_unit].iterrows():               df.at[i,col_name] = '{}'.format( (float(row[col_name].split('M')[0])) *1000000)          df[col_name] = pd.to_numeric(df[col_name])   change_to_unified_unit(df, 'views') change_to_unified_unit(df, 'author_views')
# 将清洗过的特征转化为整数df['views'] = df['views'].astype(int) df['author_views'] = df['author_views'].astype(int)

该数据集的数据类型较丰富 - 有文本型数据，如：article（正文）、title（标题）等；也包含数值型数据，如views（文章阅读量）、thumb_ups（点赞量）、类别型数据，如category（文章分类）、author（作者）等。

2.2.2 缺失值处理

这个数据集本身已包含有一些数值变量，但我们也可以增加一些新的基于已有特征而统计得到的新的数值变量。增加数值特征的同时，可以看一下哪些特征空值多，从而不考虑建立对应的长度的新变量。

df.isnull().sum() / len(df) * 100

link 0.00
author 0.00
title 0.00
category 0.00
summary 36.60
article 0.75
date 0.00
author_des 7.35
views 0.00
thumb_ups 0.00
stars 0.00
image_nos 0.00
comments 0.00
comment_nos 0.00
author_article_nos 0.00
author_views 0.00
tags 0.00
dtype: float64

可以看到summary的空值量占了36.88%，占比很大。所以在数值特征中，加入title长度和article长度2个特征（就不选择summary的长度作为新特征了）。（当然也可以选择去掉含有空值的样本，再对剩下的样本进行分析。由于这里，我之后希望对于article（正文）进行分析，所以这里只对于article去除含有空值的行。）

df = df.dropna(subset=['article'])
selected_df = df[['views','thumb_ups','stars','image_nos','comment_nos','author_views']]selected_df['title_len'] = df['title'].astype(str).str.len()selected_df['article_len'] = df['article'].astype(str).str.len()

这里选择了所有的数值型数据，并且还增加了title_len（标题长度）、article_len（正文长度）2个特征。

2.2.3 继续特征选择

其实上面已经进行了一些特征选择了，这里继续选择。

print(selected_df.shape)print(selected_df.head(0))

(1985, 8)
Empty DataFrame
Columns: [views, thumb_ups, stars, image_nos, comment_nos, author_views, title_len, article_len]
Index: []

2.2.3.1 方差

这里设定一个阈值，大于阈值的方差对应的特征可以保留下来。这里先去除方差最小的comment_nos特征。

selected_df.var()

views 4.027642e+08
thumb_ups 6.350949e+02
stars 1.457187e+04
image_nos 8.442407e+01
comment_nos 3.367118e+01
author_views 1.031604e+14
title_len 4.000153e+01
article_len 5.293931e+06
dtype: float64

2.2.3.2 相关性

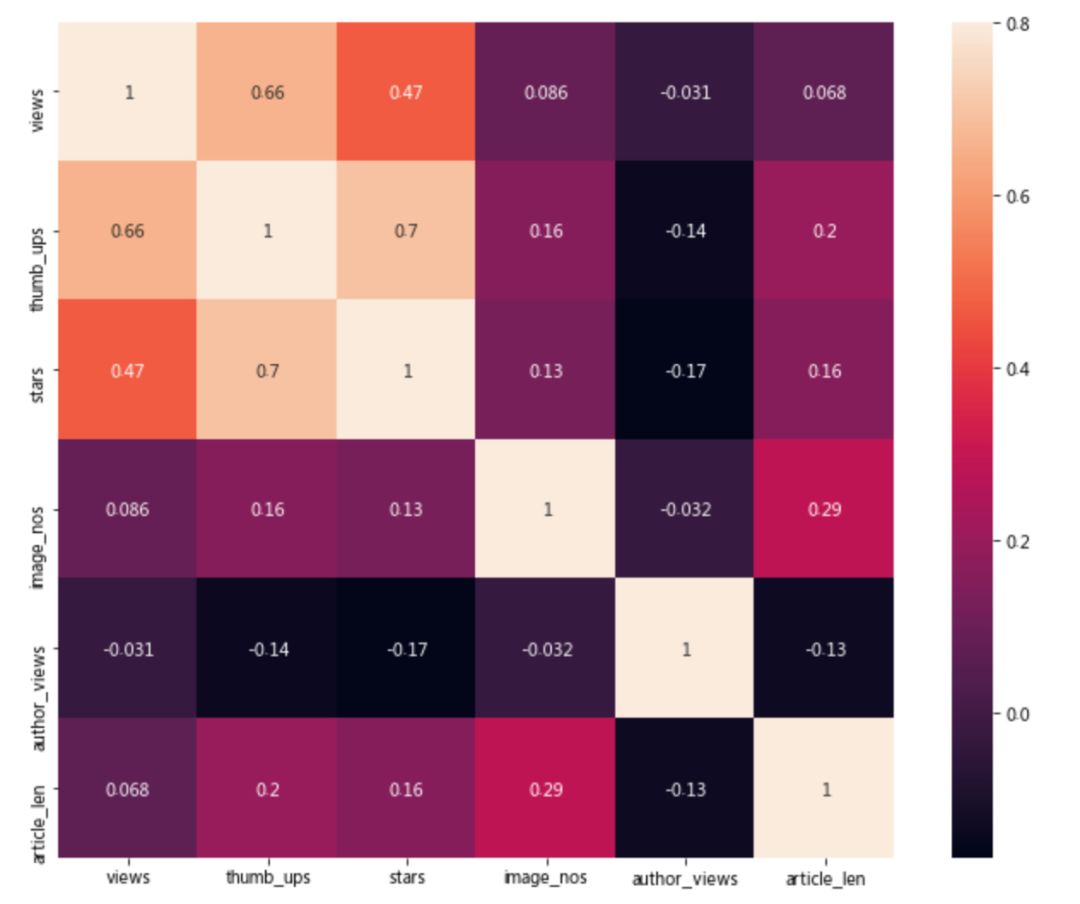
import matplotlib.pyplot as pltimport seaborn as snscorr_df = selected_df[['views','thumb_ups','stars','image_nos','author_views', 'article_len']]corr_matrix = corr_df.corr()f, ax = plt.subplots(figsize=(12, 9))sns.heatmap(corr_matrix, vmax=0.8, square=True, annot=True,ax = ax)plt.show()

可以看到thumb_ups与stars的相关性为0.7, views与thumb_ups的相关性为0.66，views与stars的相关性为0.47都远远高于别的的相关性。可以考虑去掉某个或某几个特征。

由于随机森林、前向特征选择/反向特征消除方法需要目标值的参与，这里使用的是无标记的数据，暂时无法使用。

以上大致展示了使用基于特征选择的降维处理~

在接下来的原理分析中，为了方便阅读，尽量避免了深奥的数学知识，如有不精准的描述，还请指正~

3 直接使用降维分析

3.1 降维方式列举

3.1.1 FA

从多个变量中提取共性因子，并得到最优解。在因子分析中，我们将变量按其相关性分组，即特定组内所有变量的相关性较高，组间变量的相关性较低。这里每个组就被称为一个factor。

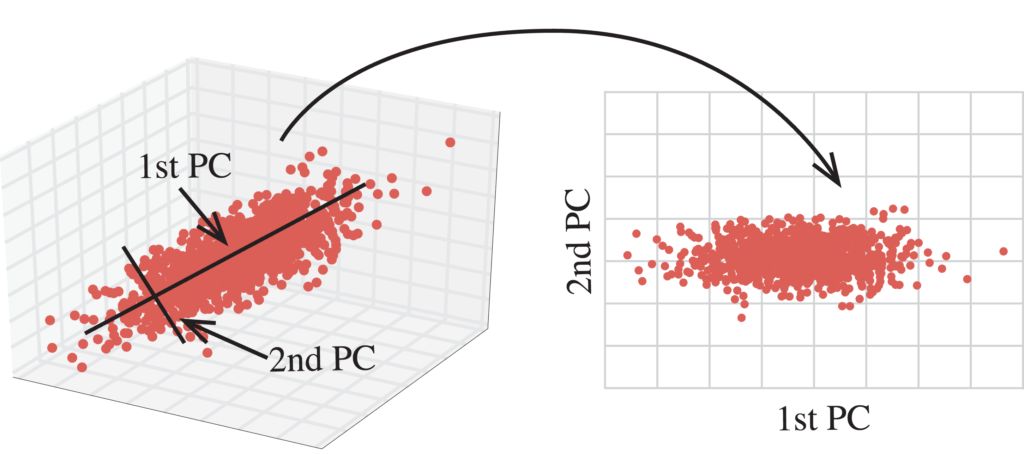
3.1.2 PCA

通过正交变换将原始的n维数据集变换到一个新的、被称做主成分的数据集中，即从现有的大量变量中提取一组新的变量。下面是关于PCA的一些要点：主成分是原始变量的线性组合。第一个主成分具有最大的方差值。第二主成分试图解释数据集中的剩余方差，并且与第一主成分不相关（正交）。第三主成分试图解释前两个主成分等没有解释的方差。（PCA算法实现使用到了SVD）。

3.1.3 ICA

ICA是基于信息论的方法。ICA和PCA的区别是：PCA寻找不相关的因子，ICA寻找独立的因子。如果2个变量不相关的，那么他们之间没有线性关系；如果2个变量独立的，那么他们不依赖于其它变量。ICA假设给出的变量是一些未知的潜在变量的线性组合，并且这些潜在变量之间互相独立。（而常用用来衡量独立的是Non-Gaussianity方法。数学不谈。）

3.1.4 ISOMAP

如果一个流形对任何方向都连续可微,那么就称为是一个smooth（平滑）/differentiate（可微）的流形。ISOMAP假定处理的流形都是平滑的。ISOMAP也假定任何流形上的一对点，geodesic distance（在曲面上两点间的最短距离）和euclidean distance（在直线上两点间的最短距离）是一样的。

详细经过：

获得neighborhood graph。计算每一对点的距离。确定哪些点作为流形的neighbors。最后这些点构成了一个neighborhood graph。（点作为顶点、距离作为边。）
计算流形中每一对点的graph distance。graph distance就是图中每一对点之间的最短路径距离。
得到这些距离后，得到一个n * n的squared graph distance矩阵。选择embedding vectors来最小化geodesic distance和graph distance的差别。最后将整个图嵌入到新的平面中去。

3.1.5 t-SNE

t-SNE是少数可以同时保留局部和整体结构的方法。它同时在低维和高维中，计算点之间的probability similarity（概率相似性）。（即在高维和低维中，它都计算好每个点之间的conditional probability（条件概率）来代表similarity（相似性）），最后最小化概率之间的差异。

3.1.6 UMAP

UMAP（均匀流形近似和投影,Uniform Manifold Approximation and Projection for Dimension Reduction）和 t-SNE应该算是目前最好的降维算法了，能最大程度的保留原始数据的特征同时大幅度的降低特征维数。

UMAP的优势在于：

可以处理大型数据集和高维的数据
便于可视化
既保留了局部结构，也保留了整体结构，和t-SNE相比，不光保留了差不多的局部结构信息，还保留了更多的整体结构信息。

但是，和tSNE有着同样的毛病，使用UMAP更倾向于观察原始数据降维后的分布，无法对后续数据进行预测 --- 就是对于新的单条测试数据就没法直接使用UMAP使其特征维数降到指定的维数了。

话虽如此，UMAP是笔者在文本挖掘中最常使用的降维算法了，下面的实际案例笔者将会给出证明！

温馨小贴士：

如何理解投影（project）

首先确定一点：高维数据投影到低维空间可以降维。这个投影可以：1.投影到一些有意思的方向上。2.投影到manifold（流形）上。（就是认为现在看到的高维数据：其实是低维的流形数据映射到高维空间上的。）

如何理解流形（manifold）

这里引用wiki的解释，它举了个地球的例子，非常直观！

流形可以视为：近看起来，像欧几里得空间或其他相对简单的空间的物体。比如：很久以前，大家认为地球是平的。那是因为，不管你在地球的哪里，它总是看起来是平的。但是如果你一直朝着一个方向走，那么最终会走到起始点。所以，认为地球是平的，那是因为人和地球相比太渺小。所以，尽管知道地球实际上差不多是一个圆球，如果只需要考虑其中微小的一部分上发生的事情，比如：测量操场跑道的长度或进行房地产交易时，仍然把地面看成一个平面。一个理想的数学上的球面（比如：理想上的地球）在足够小的区域上的特性就像一个平面，这表明它是一个流形。正如地图集和地球的关系（如果将整个地球的各个地区的地图合订成一本地图集，那么在观看各个地区的地图后，就可以在脑海中“拼接”出整个地球的景貌。），在数学中，也可以用一系列“地图”（称为坐标图或坐标卡）组成的“地图集”（atlas, 亦称为图册）来描述一个流形。而“地图”之间重叠的部分在不同的地图里如何变换，则描述了不同“地图”的相互关系。描述一个流形往往需要不止一个“地图”，因为一般来说流形并不是真正的欧几里得空间。举例来说，地球就没法用一张平面的地图来合适地描绘。

3.2 降维示例code

因为这个系列的文章都是涉及文本挖掘的，所以笔者在这里使用文本数据，该数据已经经过分词处理，直接进行特征提取和降维即可。

import pandas as pdfrom sklearn.feature_extraction.text import TfidfVectorizerdf = pd.read_excel('/home/kesci/input/cluster_dataset8319/1000-samples.xlsx')

提取文本数据的tf-idf特征：

tfv = TfidfVectorizer()x_tfv = tfv.fit_transform(df['clean_sentence'])x_tfv_array = x_tfv.toarray()

编写数据可视化函数：

import matplotlib.pyplot as pltdef check_variables_correlated(data):        plt.scatter(data[:,0], data[:,1])        plt.scatter(data[:,1], data[:,2])        plt.scatter(data[:,2], data[:,0])    def check_large_scale(data):        plt.scatter(data[:,0], data[:,1])

这里提前定义好降维效果好坏的2种衡量方法，从以下2个方面着手：

降维到3维，看各个维度之间得到的新的特征是否是之间不相关的。如果相关的话，那么两两特征作图的话，这些图重合的部分大。
降维到2维，看整体数据是否是分布的有明显的分类的界限的。

载入分析时会用到的降维方法：

from sklearn.decomposition import FactorAnalysisfrom sklearn.decomposition import PCAfrom sklearn.decomposition import TruncatedSVD from sklearn.decomposition import FastICA from sklearn.manifold import Isomap from sklearn.manifold import TSNE import umap

将多个降维方法集成在一个函数中，便于调用：

def get_decomposited_data(method, dimension, data):    return {        'FA': FactorAnalysis(n_components = dimension).fit_transform(data),        'SVD': TruncatedSVD(n_components = dimension).fit_transform(data),     'ICA': FastICA(n_components = dimension).fit_transform(data),        'ISOMAP': Isomap(n_components = dimension, n_jobs = -1).fit_transform(data),        't-SNE': TSNE(n_components = dimension).fit_transform(data),        'UMAP': umap.UMAP(n_components = dimension).fit_transform(data) }.get(method)

先看看因子分析的降维效果如何：

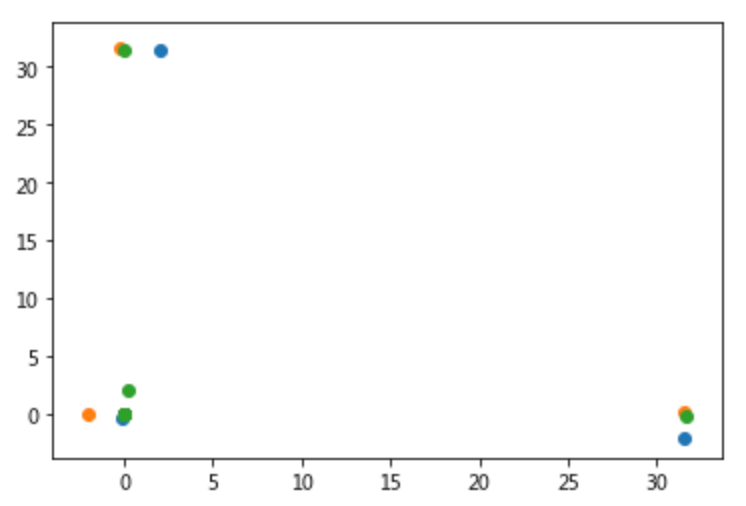
fa_3 = get_decomposited_data('FA', 3, x_tfv_array)check_variables_correlated(fa_3)

再看看SVD算法的降维效果如何：

svd_3_2 = get_decomposited_data('SVD', 3, x_tfv_array)check_variables_correlated(svd_3_2)

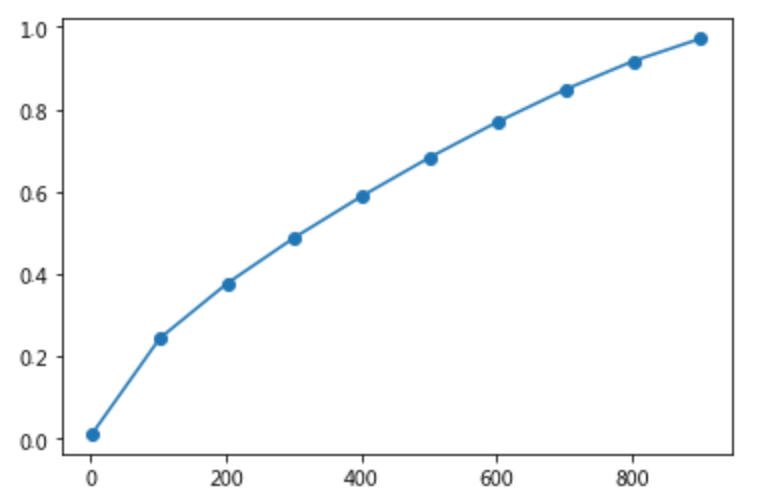
接下来，观察SVD在不同n_components下的解释度如何，不出意外，n_components值越大，解释度越高，因为保留的维度信息越多。

ratios = []n_components = [i for i in np.arange(2, 1000, 100)]for i in n_components:       ratios.append(TruncatedSVD(n_components = i).fit(x_tfv_array).explained_variance_ratio_.sum())   plt.plot(n_components, ratios, 'o-')

这里特别说明一下，像PCA、SVD都是可以通过explained_variance_ratio_来看降维在不同低维度下的最大解释值，可以表现出原数据的多少百分比的信息，既保留原有信息的强度。比如上面的例子，降维到800维的话，即可保留原数据90%以上的信息，而直接采用tf-idf特征，维数就是保留词汇的数量了，为保证模型的准确度，维度起码得10000维起步~

再试试ICA、ISOMAP和t-SNE：

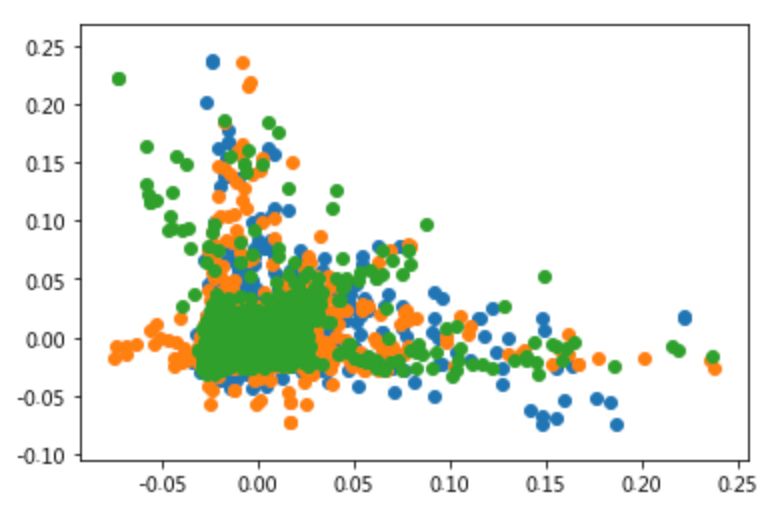
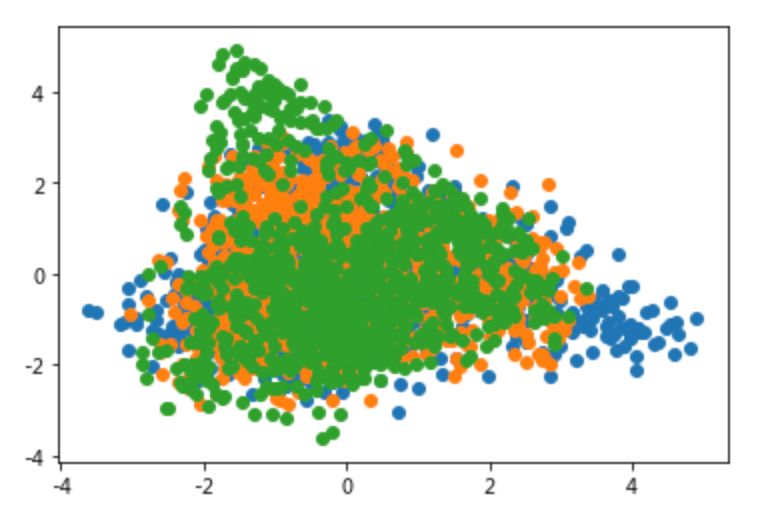
ica_3 = get_decomposited_data('ICA', 3, x_tfv_array)check_variables_correlated(ica_3)

isomap_3 = get_decomposited_data('ISOMAP', 3, x_tfv_array)check_variables_correlated(isomap_3)

tsne_3 = get_decomposited_data('t-SNE', 3, x_tfv_array)check_variables_correlated(tsne_3)

最后是时新的UMAP：

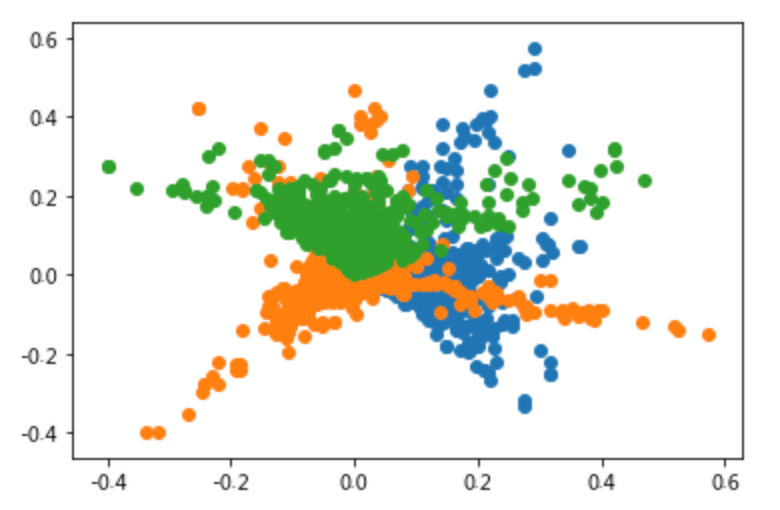
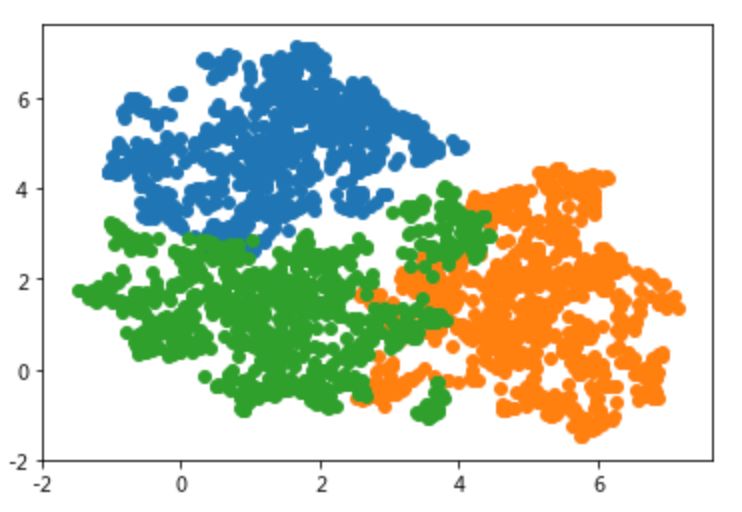
umap_3_2 = get_decomposited_data('UMAP', 3, x_tfv_array)check_variables_correlated(umap_3_2)

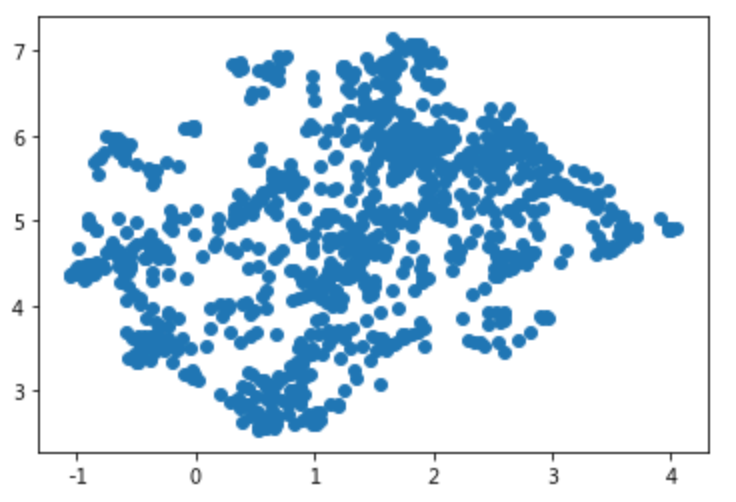
check_large_scale(umap_3_2)

从上面的文本数据降维效果来看，UMAP最大限度的隔离开了不同类别的数据点，区分效果良好，后面使用聚类算法的话，也将取得不错的效果，这也是笔者为何钟情于该降维算法的原因了！

结语

机器学习界有句至理名言“no free lunch（天下没有免费的午餐）”，搁这里讲就是 --- 不同的降维方式对于不同的特征数据有着不同的适用性，说人话就是，不同类型的数据有着对应的降维方式适用，所以说降维算法的选择上，得具体问题，具体分析！。

我在后面的案例中选择TF-IDF特征，拍脑袋选择3维作为目标降维数量，比较了几类降维算法的降维效果，最终是UMAP效果最好，当然这是针对这个人人都是产品经理的文本数据集来说的。

同时，通过最后绘制出的2维平面图来看大致的数据点分布，也可以看到数据点的稠密度不高，区分度较好。仅从这一点来看，在文本数据的降维场景下，选择UMAP是不错的选择！

推荐阅读

文心（ERNIE）3项能力助力快速定制企业级NLP模型，EasyDL全新升级！

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。