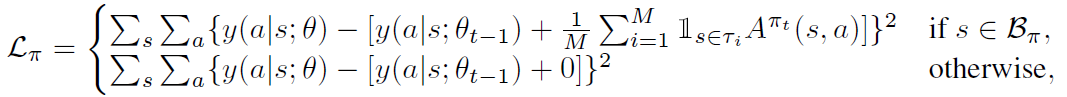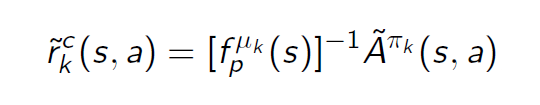ICLR 2022 | 绝艺学会打麻将，腾讯AI Lab提出全新策略优化算法ACH

感谢阅读腾讯AI Lab微信号第144篇文章。本文介绍「绝艺」在二人麻将游戏环境取得的进展，相关算法及benchmark已开源，论文被机器学习国际顶会 ICLR 2022 接收。

「绝艺」是腾讯AI Lab研发的棋牌类AI。自2016年面世后，它已四次夺得世界顶级围棋赛事冠军，包括UEC杯、AI龙星战、腾讯世界人工智能围棋大赛、世界智能围棋公开赛等，并自2018年起无偿担任中国国家围棋队训练专用AI。

在围棋以外，腾讯AI Lab「绝艺」团队持续深入研究大规模二人零和博弈问题，从完美信息游戏（围棋）逐步拓展至非完美信息游戏（麻将等）。

4月25日，腾讯AI Lab宣布棋牌类AI「绝艺」取得新突破，在1v1麻将（二人雀神）测试中战胜职业冠军选手。团队在大规模强化学习算法框架下提出了一个新的策略优化算法Actor-Critic Hedge (ACH)，部分解决了大规模深度强化学习自博弈收敛不到纳什均衡最优解的问题。该算法及对应二人麻将benchmark已通过论文开源，并被机器学习顶会ICLR 2022收录。

论文链接：

https://openreview.net/pdf?id=DTXZqTNV5nW

非完美信息博弈广泛存在于日常生活的方方面面，如智慧交通、网络安全、金融分析等。腾讯AI Lab以麻将AI为切入点研究非完美信息博弈，其目标不仅限于打造世界级的国粹麻将AI，更多的在于探索非完美信息博弈在游戏领域，以及其他广阔的社会生活领域的实际应用价值。

研究背景

棋牌游戏一直以来都是AI技术的优质试验场，例如，在围棋环境中就诞生了AlphaGo、绝艺等标杆性的AI。

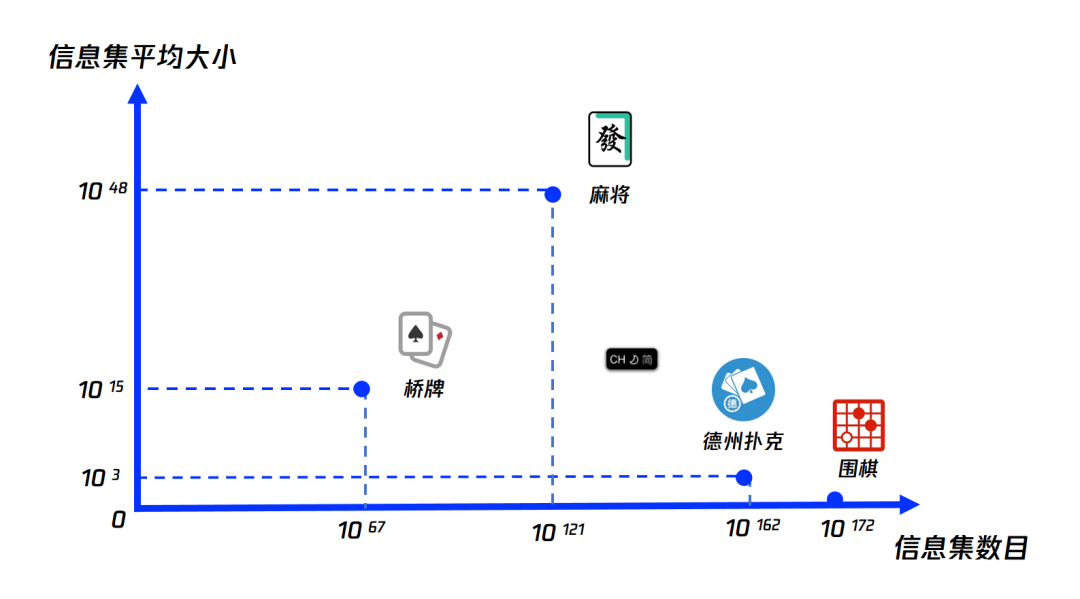
相比于围棋这类「完美信息」游戏，德州扑克，桥牌，麻将这类「非完美信息」游戏存在着大量的隐藏信息，例如，玩家无法直接知道对手的手牌，这给游戏带来了更高的不确定性，对AI的博弈能力提出更高要求。

具体而言，在完美信息游戏中，始终存在确定性的最优解，即任何状态下都存在一个固定的最优动作。然而在非完美信息游戏中，最优策略往往是随机化的。

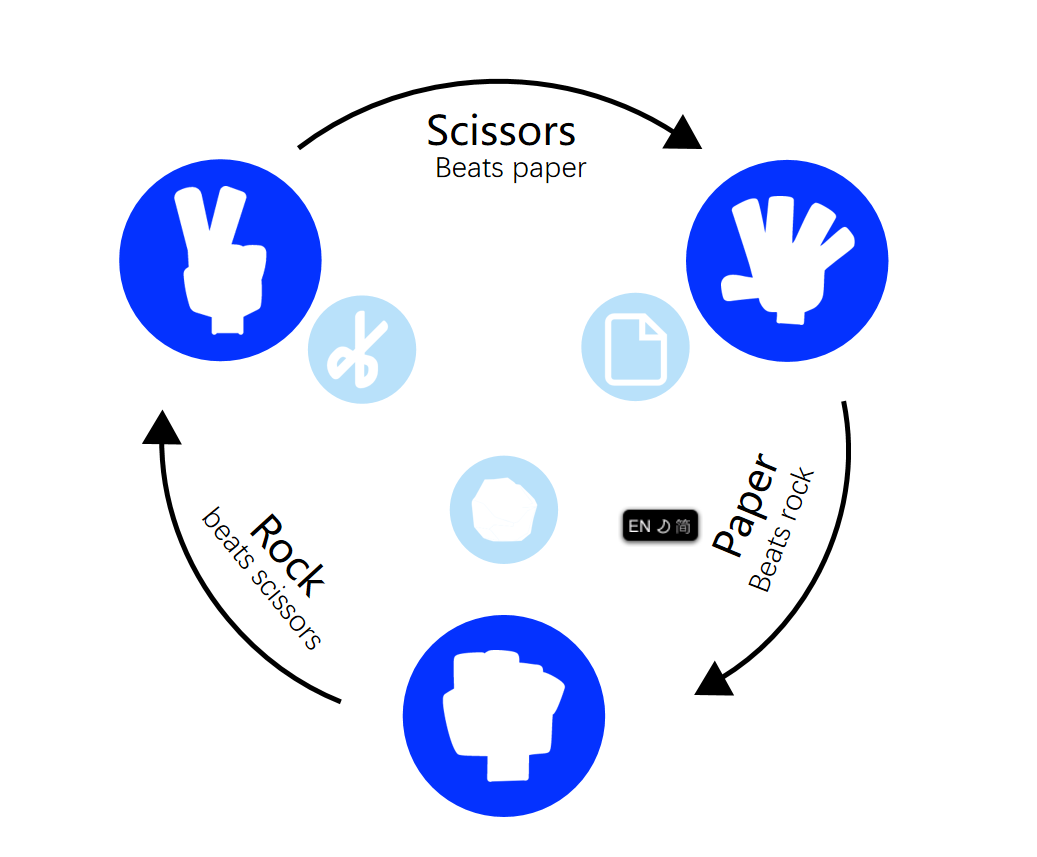
例如，在二人「石头-剪刀-布」游戏中，最优策略（纳什均衡策略）不再是某一个固定的动作，而是关于每个动作的一个概率分布：等概率出石头，剪刀，和布。

二人「石头-剪刀-布」

近年来，反事实遗憾值最小化算法（CFR）在德州扑克游戏AI上取得了一系列突破性进展，例如DeepStack（2017 Science杂志），Libratus（冷扑大师，2017 Science杂志），和Pluribus（2019 Science杂志）。CFR具有收敛到纳什均衡解的理论保证。

然而，由于CFR是一种基于表格的算法，并且需要对游戏树做全遍历，CFR在德州扑克游戏上的应用需要大量的领域知识来对游戏树做剪枝。虽然后续有一些工作尝试将深度学习和CFR做结合，但目前还没有看到CFR在其他大规模非完美信息游戏上的成功应用。

另一方面，由于深度强化学习高效的可扩展性，深度强化学习结合自博弈广泛用于大规模非完美信息游戏中求解高强度AI，例如王者荣耀、星际争霸2、Dota2等。

然而，基于深度强化学习的大部分AI的鲁棒性有待提高，集中表现为AI容易被针对，最坏情况下的性能没有保证。这些问题的根本原因在于深度强化学习结合自博弈缺乏收敛到纳什均衡解的理论保证。

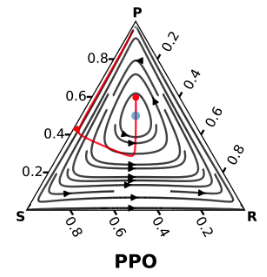
例如下图所示，在一个简单的二人石头-剪刀-布游戏中，自博弈Proximal Policy Optimization无法收敛到（红线为收敛过程）纳什均衡解（蓝点）。

  

方法简介

腾讯AI Lab「绝艺」团队的研究结合经典反事实遗憾值最小化算法CFR的思想，在大规模强化学习算法框架下提出了一个新的策略优化算法Actor-Critic Hedge (ACH)。该算法一方面具备深度强化学习方法的可扩展性，一方面在某些条件下具备收敛到纳什均衡解的理论保证。

具体来说，团队修改传统深度强化学习策略网络的损失函数：从最大化累计奖励到拟合累计采样advantage：

累计采样advantage与CFR中的累计遗憾值存在一定的等价关系。另外，可以证明，相比过去基于采样regret的方法，采样advantage有更小的variance：

更小的variance在基于神经网络的方法中意味着更稳定的效果。ACH具体算法流程如下：

在该工作中，团队引入了一类新的CFR算法：Weighted CFR。Weighted CFR有如下定义：

算法ACH可以看作是一类基于神经网络的Weighted CFR算法的一个高效实现。我们证明了Weighted CFR的算法收敛性，进而近似证明了ACH的算法收敛性：

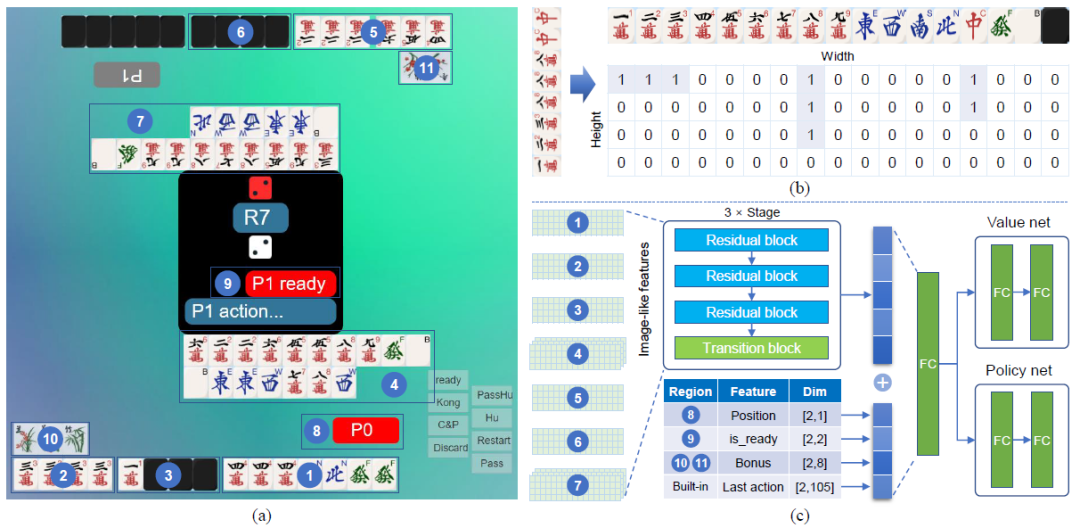
另外，针对1v1麻将的具体神经网络设计如下：

在对比主流方法的基础上，该算法的优越性在1v1麻将（战胜职业冠军）和1v1德州扑克上均得到了验证。

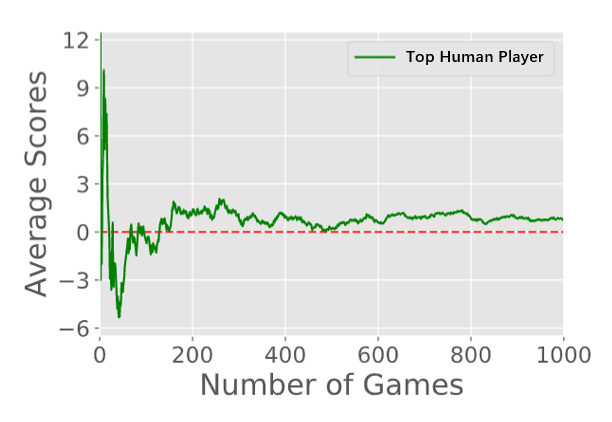
1v1麻将（二人雀神）测试中，「绝艺」与世界冠军职业选手对战1000回合，平均赢番0.82

（标准差0.96，单边 t 检验的 p value 为0.19）

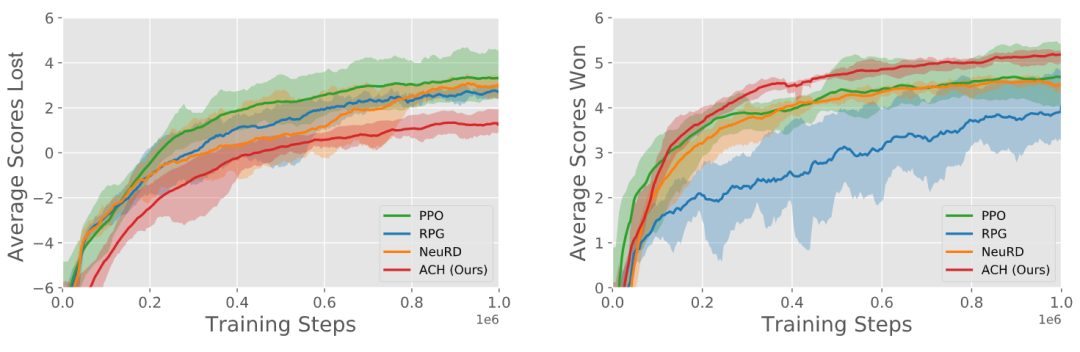
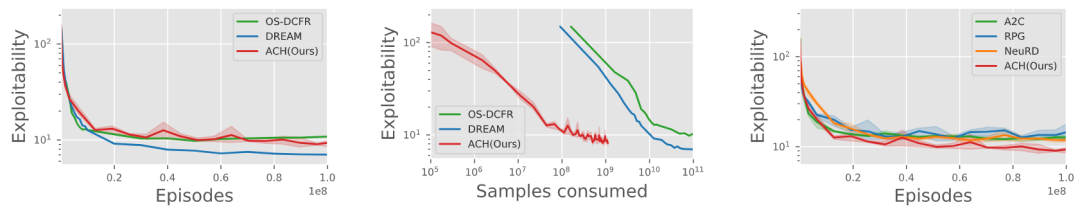
1v1麻将环境，主流算法性能对比

1v1简单德扑环境，各种经典反事实遗憾值最小化算法扩展的对比

* 欢迎转载，请注明来自腾讯AI Lab微信（tencent_ailab）