伯奇和斯温纳顿- 戴尔猜想:皇冠上的明珠
数学是研究数量、结构、变化以及空间模型等概念的一门学科。作为人类思维的表达形式,数学反映了人们探寻真理的意志、缜密周详的逻辑以及对完美境界的追求。因此,数学成了一切自然科学的基础。
在国际象棋的博弈中,威力最大的棋子就是皇后,甚至国王也远逊于皇后的特权。因此德国数学家高斯(Gauss)盛赞“数学是科学的皇后”。在数学研究的所有领域中,数论则被认为是皇后的皇冠。
图1 高斯和他的名言(图片来源:azquotes.com)
事实上,古希腊人对数学最早的研究正是伴随着对数论的兴趣而生。在历经2000多年的发展后,数论作为最古老的学科已经积累了大量珍贵的理论财富,且依然在今天引领着数学研究的潮流。数论的核心问题就是认清整数的特性,尤其是素数的本质。无数最杰出的数学家都曾经潜心于对自然数如痴如醉的研究之中,试图在这条奔腾不息的整数河流里找到隐藏着的宝藏。
时至今日,数学中所有的重要学科都已经在现实生活里找到了巨大的应用前景。唯有数论还只是犹抱琵琶半遮面,遮遮掩掩地不肯敞开内心的大门。偶尔从大门里投射出来的金光已经让门外的人目眩神迷、心驰神往。素数的第一次小试牛刀就在信息、金融和国防安全体系中占据了核心的地位。为现代化国家保障国民安全的体系就系于素数的分布规律之上。
在数论的王国里,有无数的瑰宝已经找到它心仪的主人。陈景润因为证明“1+2”,成为哥德巴赫猜想的守护星。英国数学家怀尔斯(Wiles)则在1994年彻底解决了困扰世人358年的费马(Fermat)猜想。张益唐则在破译数学史上最古老的“孪生素数猜想”中迈出了至关重要的一步。这些理论的巨大成就,已经极大地拓展了数学家的视野,其发展的理论方法,不啻为人类智慧的巅峰贡献。尽管如此,仍然有大量绚丽的瑰宝还在等待着后人去发掘。如今,在数论领域叱咤风云的黎曼猜想和伯奇和斯温纳顿- 戴尔猜想则延续着数论的辉煌和挑战。特别是伯奇和斯温纳顿- 戴尔猜想,它和费马大定理一样,寄托着人们对自然数无穷无尽的好奇心和追求。
图2 英国数学家伯奇(右,1931-)和斯温纳顿-戴尔(左,1927-)(图片来源:claymath.org)
遥远的毕达哥拉斯学派
伯奇和斯温纳顿- 戴尔猜想的故事则要从古希腊的毕达哥拉斯说起。
图3 毕达哥拉斯(约570B.C.-495B.C. 图片来源:维基百科)
古希腊的毕达哥拉斯学派热衷于研究几何和数的关系,他们独立找到了被后世称为“勾股定理”的关系,该定理准确地指出了直角三角形的斜边与另外两条边的数值关系。彼时的毕达哥拉斯学派认为世间的一切数都是整数,或者是整数之比,拒绝接受无理数的存在。受到该学派的影响,人们普遍关注有理数在直角三角形的构成中所发挥的作用。
图4 勾股定理的一种几何证明(图片来源:wikihow.com)
一个经典问题于是应运而生:给定一个自然数n,是否存在一个边长为有理数而面积恰好是n的直角三角形?对此类问题的深入研究却意外地揭示了数论中迄今为止最前沿和艰深的秘密。及至近代,人们很快发现,这个问题可以等价地转化为找到一类被称为椭圆曲线的有理数解。这样,一个纯粹的数论问题,就以一种几何的形式呈现在人们面前。
椭圆曲线的魅力
自20世纪中叶以来,椭圆曲线已经成为重要的基础性数学研究的对象,它们与数学的诸多领域,包括数论、密码学、几何学等等学科都有千丝万缕的联系。特别地,怀尔斯在证明费马大定理的过程中,就强烈依赖于一类特殊的椭圆曲线的性质。伯奇和斯温纳顿- 戴尔并没有直接找到一般椭圆曲线是否存在有理数解的办法,相反,他们试图对该椭圆曲线上的所有有理数点进行计数统计。为此,他们提出了一种判定椭圆曲线是否具有无穷多个有理点的等价方法,这就是被称为伯奇和斯温纳顿- 戴尔猜想的千年难题。
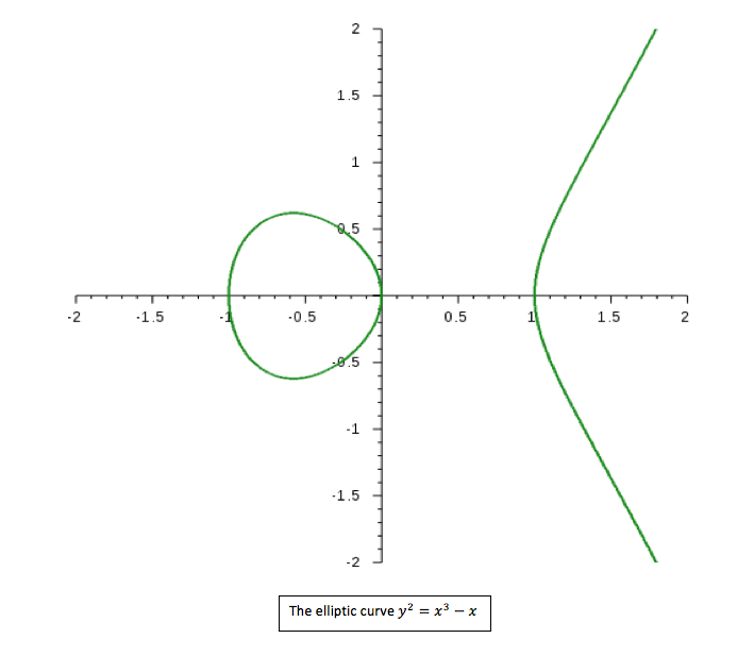
图5 椭圆曲线y2=x3-x,显然该曲线有3个有理数解(图片来源:theconversation.com)
三百多年以来,人们为了破译费马大定理耗费了无数杰出的脑力和智慧,也因此发展了无数最惊异和激动人心的工具与理论,包括椭圆曲线和模形式等等前沿工具的诞生都为现代数学注入了蓬勃的生命力,也为诸如黎曼猜想等等最耀眼的数学之谜提供了解决的希望。解决伯奇和斯温纳顿- 戴尔猜想则需要更为深刻的洞见和全新的基础理论,对它的深入研究将对现代数学所有重大的基础领域产生悠久而重大的影响。
作者单位:中国科学院数学与系统科学研究院
(文章首发于科学大院,转载请联系cas@cnic.cn)
2. 二维超导材料
4. 物理学咬文嚼字之九十八:Phase:a phenomenon
6. 物理像什么?
9. 相对论天体物理
END