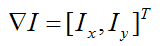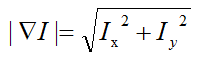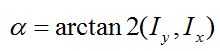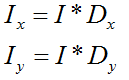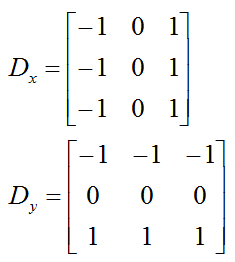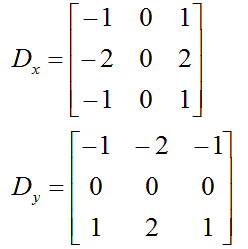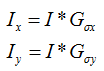【干货】计算机视觉实战系列07——用Python做图像处理

会员服务 ·

【干货】计算机视觉实战系列07——用Python做图像处理

2018 年 4 月 16 日 专知 Hui

【导读】专知成员Hui上一次为大家介绍SciPy库的使用以及图像高斯模糊实战，这一次继续为大家详细讲解SciPy库的使用以及图像导数实战。

【干货】计算机视觉实战系列01——用Python做图像处理（基本的图像操作和处理）

【干货】计算机视觉实战系列02——用Python做图像处理（Matplotlib基本的图像操作和处理）

【干货】计算机视觉实战系列03——用Python做图像处理（Numpy基本操作和图像灰度变换）

【干货】计算机视觉实战系列04——用Python做图像处理（图像的缩放、均匀操作和直方图均衡化）

【干货】计算机视觉实战系列05——用Python做图像处理（主成分分析）

【干货】计算机视觉实战系列06——用Python做图像处理（图像高斯模糊分析）

SciPy库的应用——图像导数实战

SciPy

SciPy是建立在NumPy基础上，用于数值运算的开源工具包。SciPy提供很多高效的操作，可以实现数值积分、优化、统计、信号处理，以及对我们来说最重要的图像处理功能。接下来，本节会介绍SciPy中大量有用的模块。SciPy是一个开源工具包，可以从http://scipy.org/Download下载。

图像导数

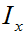
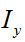
在整个图像处理的学习过程中可以看到，在很多应用中图像强度的变化情况是非常重要的信息。强度的变化可以用灰度图像I（对于彩色图像，通常对每个颜色通道分别计算导数）的x和y的方向导数和进行描述。

图像的梯度向量为：

梯度有两个重要的属性，一个是梯度的大小：

它描述了图像变化的强弱，一是梯度的角度：

它描述了图像中在每个点（像素）上强度变化最大的方向。NumPy中的arctan2()函数返回弧度表示的有符号角度，角度的变化区间为。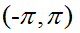

我们可以用离散近似的方式来计算图像的导数。图像的导数大多可以通过卷积简单地实现：

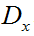
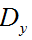
对于和，通常选择Prewitt滤波器：

Prewitt边缘算子是一种边缘样板算子，利用像素点上下，左右邻点灰度差，在边缘处达到极值检测边缘，对噪声具有平滑作用。由于边缘点像素的灰度值与其领域点像素的灰度值有显著不同，在实际应用中通常采用微分算子和模板配匹方法检测图像的边缘。

或者使用Sobel滤波器，Sobel算法是一种较成熟的微分边缘检测算法，它计算简单，且能产生较好的检测效果，对噪声具有平滑作用，可以提供较为精确的边缘方向信息。

Sobel算子是一阶导数的边缘检测算子，使用两个方向算子(垂直算子和水平算子)，对图像进行卷积运算，得到两个矩阵，再求这两个矩阵对应位置的两个数的均方根，得到一个新的矩阵，即为灰度图像矩阵中各个像素点的梯度值。在算法实现过程中，通过3×3模板作为核与图像中的每个像素点做卷积和运算，然后选取合适的阈值以提取边缘。

其实图像的梯度可以用一阶导数和二阶偏导数来求解。但是图像以矩阵的形式存储的，不能像数学理论中对直线或者曲线求导一样，对一幅图像的求导相当于对一个平面、曲面求导。对图像的操作，我们采用模板对原图像进行卷积运算，从而达到我们想要的效果。而获取一幅图像的梯度就转化为：模板（Roberts、Prewitt、Sobel、Lapacian算子）对原图像进行卷积，不过这里的模板并不是随便设计的，而是根据数学中求导理论推导出来的。

这些导数滤波器可以使用scipy.ndimage.filters模块的标准卷积操作来简单地实现。

代码为：

from PIL import Image
from numpy import *
import matplotlib.pyplot as plt
from scipy.ndimage import filters

im = array(Image.open('test.jpg').convert('L'))

imx = zeros(im.shape)
filters.sobel(im, 1, imx)

imy = zeros(im.shape)
filters.sobel(im, 0, imx)

magnitude = sqrt(imx ** 2 + imy ** 2)

fig = plt.figure(figsize=(30, 30))

plt.subplot(2, 2, 1)
plt.axis('off')
plt.imshow(im, plt.cm.gray)

plt.subplot(2, 2, 2)
plt.axis('off')
plt.imshow(imx, plt.cm.gray)

plt.subplot(2, 2, 3)
plt.axis('off')
plt.imshow(imy, plt.cm.gray)

plt.subplot(2, 2, 4)
plt.axis('off')
plt.imshow(magnitude, plt.cm.gray)

plt.show()

输出结果为：

上述输出结果分别是原始灰度图像、x导数图像、y导数图像、梯度大小图像

这种计算图像导数的方法有一些缺陷，在该方法中，滤波器的尺度需要随着图像分辨率的变化而变化。为了在图像噪声方面更稳健，以及在任意尺度上计算导数，我们使用高斯导数滤波器：

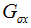
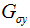
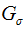
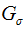
其中和表示在x和y方向上的导数，为标准差为σ的高斯函数。

我们之前用于模糊的filters.gaussian_filter()函数可以接受额外的参数，用来计算高斯导数。可以简单的按照下面的方式来处理：

from PIL import Image
from numpy import *
import matplotlib.pyplot as plt
from scipy.ndimage import filters

im = array(Image.open('test.jpg').convert('L'))

sigma = 3  # 标准差

imx = zeros(im.shape)
filters.gaussian_filter(im, (sigma, sigma), (0, 1), imx)

imy = zeros(im.shape)
filters.gaussian_filter(im, (sigma, sigma), (1, 0), imy)

fig = plt.figure(figsize=(30, 30))

plt.subplot(1, 3, 1)
plt.axis('off')
plt.imshow(im, plt.cm.gray)

plt.subplot(1, 3, 2)
plt.axis('off')
plt.imshow(imx, plt.cm.gray)

plt.subplot(1, 3, 3)
plt.axis('off')
plt.imshow(imy, plt.cm.gray)

plt.show()