图神经网络的表达能力，究竟有多强大？

会员服务 ·

图神经网络的表达能力，究竟有多强大？

2020 年 8 月 15 日 AI科技评论

作者 | Mr Bear

编辑 | 丛末

近年来，随着图神经网络在各个领域的火热应用，越来越多的学者试图从图论的角度对图神经网络的表达能力进行理论分析，并基于这些理论分析开发出了性能强大的模型。然而，在实际应用中，这些在理论上非常强大的模型的性能往往会受到计算复杂度等因素的限制。

本文作者 Michael Bronstei n 是一名来自帝国理工学院的教授，同时也是 Twitter 图机器学习项目组的负责人。在本文中，他深入浅出地介绍了近年来分析图神经网络表达能力的工作，并介绍了他们对于该领域未来发展方向的思考。

1

图神经网络和 WL 图同构测试之间的关系

众所周知，传统的前馈神经网络（多层感知机）是一种通用函数近似器：它们能够以任意的准确率逼近任意的平滑函数。对于近期兴起的图神经网络来说，其表征性质还不太为人所知。在实验中，我们经常可以看到图神经网络在某些数据集上性能优异，但同时又在另一些数据集上表现令人失望。

为了探究造成这种现象的根本原因，我们不得不思考一个问题：图神经网络究竟有多强大？

在探究这一问题的过程中，我们所面临的一个挑战是：实际应用场景下使用的图往往是连续结构和离散结构（节点、边特征、连通性）的组合。因此，该问题可以被表述为不同的形式。一种可能的形式化定义是：图神经网络是否能够区分不同类型的图结构。在图论中，这是一种被称为「图同构问题」的经典问题，旨在判断两个图在拓扑意义上是否等价。两个同构的图拥有相同的连通性，其差别仅仅可能是节点的排列不同。

稍令人惊讶的是，我们尚不知晓精确的图同构问题的复杂度级别。该问题在多项式时间内不可解，它也不是一个 NP 完全（NPC）问题。有时，我们将其复杂度称为一种特殊的「GI 级」（GI class）。

1、Weisfeiler-Lehman 测试

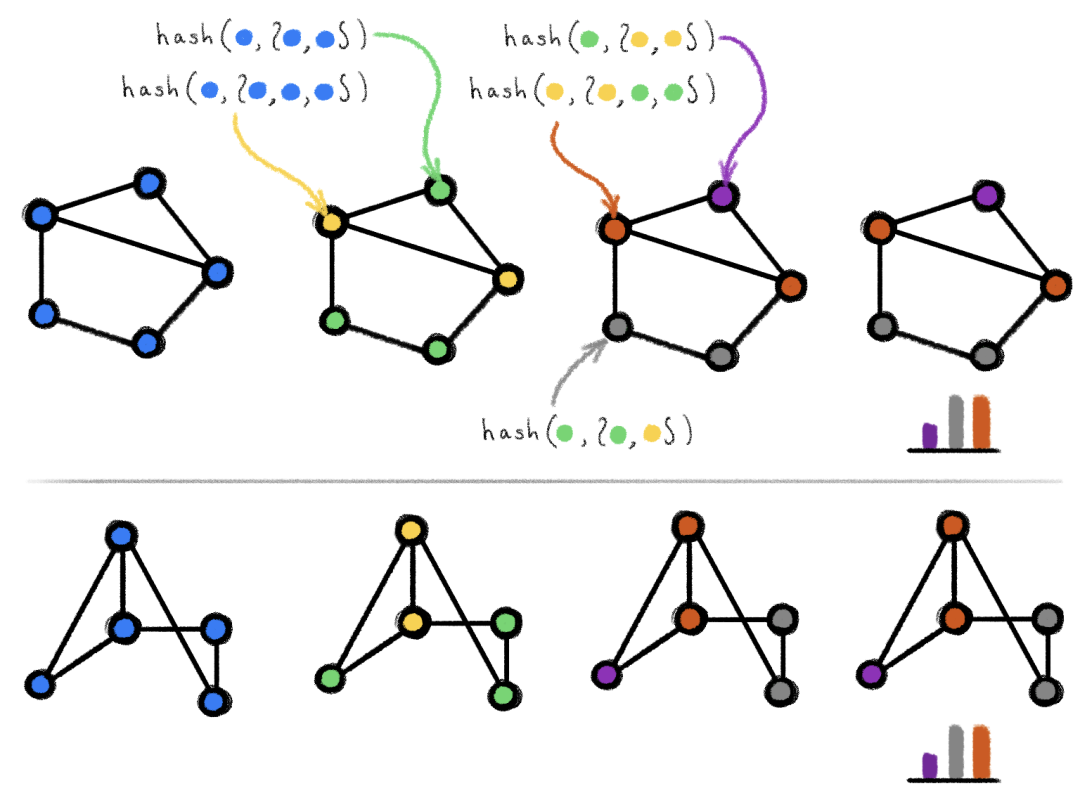
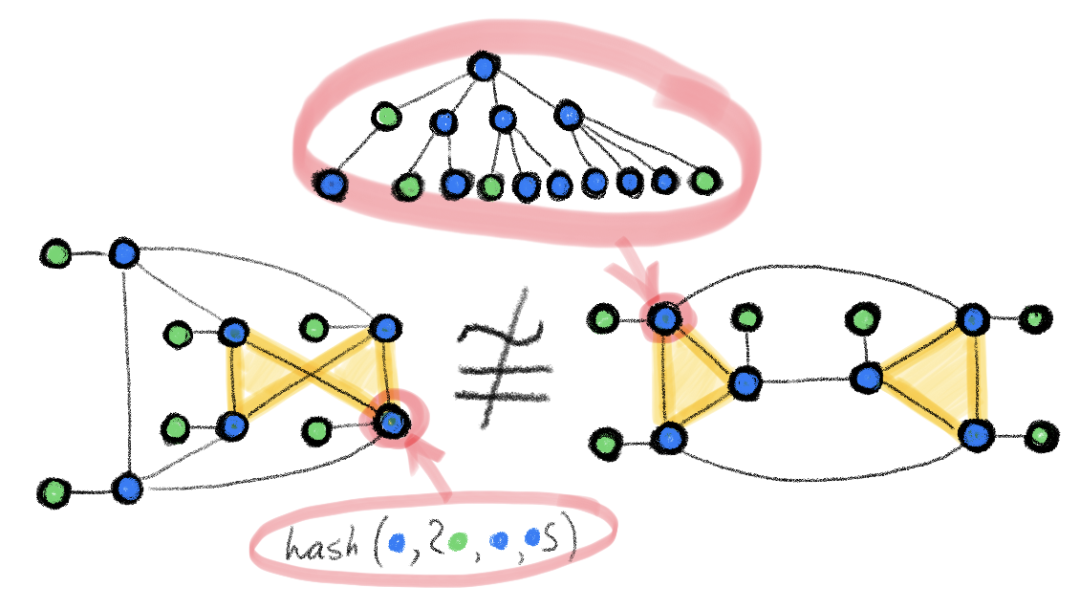
Boris Weisfeiler 和 Andrey Lehman 于 1968 年发表的具有开创性意义的论文「The reduction of a graph to canonical form and the algebra which appears therein 」），提出了一种高效的启发式算法，我们现在将其称为「WL 测试」。

最初，人们认为 WL 测试可以在多项式时间内求解图同构问题。但一年之后，人们就举出了一个反例。然而，从概率意义上说，似乎 WL 测试对于几乎所有的图都有效。

图 1：在两个同构图上执行 WL 测试的示例。包含弧线的 hash 圆括号代表多重集。在着色情况不再变化后算法会终止，并给出输出结果（颜色直方图）。若将两图输入给该算法得到的输出相同，则说明两图可能同构。

WL 测试是建立在迭代式的图重着色（图论中的「着色」指的是一种离散的节点标签）基础上的，在初始状态下，每个节点的颜色均不相同。在每一步迭代中，算法会聚合节点及其邻居节点的颜色，并将它们表征为多重集，然后将聚合得到的颜色多重集通过 Hash 函数映射到某种唯一的新颜色上。当达到稳定的着色状态（各节点着色状态不再变化）后，算法终止。当算法终止后，若两图的着色情况不同，则我们认为它们「非同构」。如果两图着色情况相同，它们可能（但并不一定）是同构的。换句话说，WL 测试是图同构的必要非充分条件。有一些非同构的图在接受 WL 测试后得到的着色情况也是相同的，而在这种情况下 WL 测试就失效了，因此我们只能认为它们「可能同构」。下图展示了其中的一种可能性：

图 2：显然，WL 图同构测试会为上面的两个非同构图生成相同的着色结果，此时 WL 测试失效。在化学领域中，这两个图分别代表两种不同的化合物「decalin」（左图）和「bicyclopentyl」（右图）的分子结构。

2、图同构网络（GIN）

Keyulu Xu 等人发表的论文「 How powerful are graph neural networks?」和 Christopher Morris 等人发表的论文，以及 Thomas 在他至少两年前撰写的博客「GRAPH CONVOLUTIONAL NETWORKS」，中注意到，WL 测试与图消息传递神经网络有惊人的相似之处，它们都在图上进行了一种类似于卷积的操作。

相关论文/文章链接：

https://arxiv.org/abs/1810.00826

https://tkipf.github.io/graph-convolutional-networks/

在一个消息传递层中，每个节点的特征会以聚合其邻居节点特征的方式被更新。对聚合和更新操作的选择是十分重要的：只有使用多重集的单射函数才能使其与 WL 算法等价。在前人的研究中，「取最最大值」或「取均值」等聚合操作都是一定弱于 WL 的能力，它们甚至不能区分非常简单的图结构：

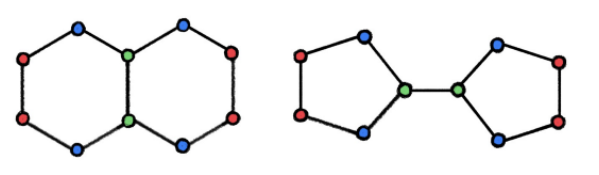
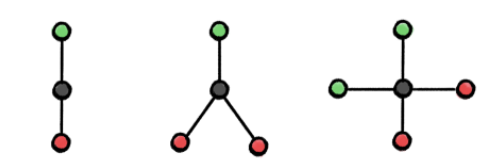
图 3：通过「取最大值」操作无法区分左图、中图、右图，通过「取均值」聚合函数可以区分左图和中图、通过「取最大值」和「取均值」操作均无法区分左图和右图。这是因为通过这些方法从黑色节点的邻居中聚合而来的特征将会是相同的。

Xu 提出了一种聚合和更新函数的选择方案，它使得消息传递神经网络与 WL 算法等价，该网络被称为「图同构网络」（GIN）。该网络和标准的消息传递神经网络一样强大。但是，GIN 不仅仅是一种新的网络架构，其主要影响在于它通过一种简单的设定形式化定义了图神经网络表达能力的问题，这种设定与图论中的经典问题相关。该网络的思路也启发了许多后续的工作。

3、Weisfeiler-Lehman 层次结构

使用更加强大的图同构测试，是扩展 Xu 和 Morris 等人工作的一个方向。因此，László Babai 提出了 k-WL 测试，这是 WL 算法在高阶上的扩展，它在 k 元组上进行操作，而非操作单个节点。除了 1-WL 和 2-WL 测试是等价的，(k+1)-WL 始终严格强于 k-WL（k≥2），即对于某些图而言 k-WL 测试失效，而 (k+1)-WL 测试可以成功判定图是否同构，但反之则不然。因此，k-WL 是一种层次结构的或随着 k 的增大而逐渐更加强大的图同构测试，有时被称为「Weisfeiler-Lehman 层次结构」。

我们可以设计出遵循 k-WL 测试的图神经网络，这种网络是一定比消息传递架构更加强大的。Morris 等人在论文「 Weisfeiler and Leman go neural: Higher-order graph neural networks 」中提出了第一种这样的架构 k-GNN。

相关论文链接：

https://aaai.org/ojs/index.php/AAAI/article/view/4384/4262

传统的消息传递神经网络和这种高阶图神经网络之间最关键的区别在于：由于 k-WL 算法在节点的 k 元组上进行操作，所以这种高阶图神经网络是非局部的（non-local）。这对算法的实现及其计算复杂度和存储复杂度都有重要的影响：k-GNN 需要 𝒪(nᵏ) 的存储空间。为了降低复杂度，Morris 基于在局部邻居节点中的信息聚合机制设计了一种 k-GNN 的局部版本，然而其表达能力要稍微弱于 k-WL。

Haggai Maron 提出了一种稍微有些不同的高阶图架构。他基于 k-阶张量定义了一类不变性图网络（IGN），说明它们与 k-WL 测试一样强大。IGN 是根据 k-WL 的另一种变体衍生而来，与 k-GNN 相比，IGN 在计算复杂度方面更具优势。具体而言，与 3-WL 等价的 IGN「仅仅」具有 n 的平方级的计算复杂度，这可能是唯一一种实际可用的严格强于消息传递架构的图神经网络，但它的复杂度与消息传递架构的线性复杂度仍然有很大的差距。

从理论的角度来看，可证明的强大图神经网络的相关工作提供了一种严谨的数学框架，它可以帮助研究者们解释并对比不同的算法。许多后继的工作使用图论和分布式局部算法中的各种方法对这些工作的结果进行了扩展。

然而，从实用的角度来看，这些新架构几乎没有产生重大的影响：例如，Bengio 等人提出的最新的对比基准说明，近期这些可证明的强大算法实际上性能要差于之前的技术。

在机器学习领域中，这并非是一种不寻常的状况。实际上，理论和实践之间往往有很大的鸿沟。其中一种可能的解释是，这是由对比基准测试本身的缺陷所导致的。但是更深层次的原因也许是，更好的表达能力并不一定意味着更好的泛化性能（有时甚至恰好相反）。此外，在具体的应用中图同构模型可能并不能正确地捕获图相似性的实际概念。可以肯定的是，这一领域的工作硕果累累，它搭建了连通其它学科的桥梁，并引入了以前在图上的深度学习领域中没有使用过的方法。

2

超越 Weisfeiler-Lehman：将子结构用于可证明的具有强大表达能力的图神经网络

图 4：图中的子结构

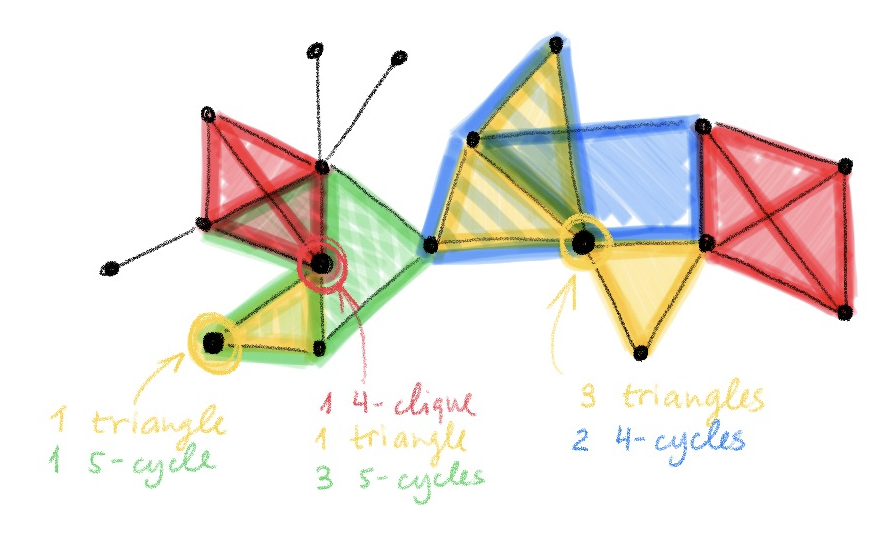
最近发表的具有开创性意义的论文「 How powerful are graph neural networks?」和「 Weisfeiler and Leman go neural: Higher-order graph neural networks 」将图神经网络和图同构测试联系了起来，并且观察到了消息传递机制和 WL 测试之间的相似性。「WL 测试」是一种对基于图论的层次化迭代式算法的统称，这类算法可以在多项式时间内求解，被用于判定图是否同构。k-WL 测试根据某些邻居节点的聚合规则，在每一步中对图中顶点的 k 元组重新着色，直到达到稳定的着色状态才终止算法。若两图的色彩直方图不同，则我们认为它们非同构；否则，两图可能（但不一定）同构。

相关论文链接：

https://arxiv.org/abs/1810.00826

https://aaai.org/ojs/index.php/AAAI/article/view/4384/4262

消息传递神经网络最多与 1-WL 测试（又称「node colour refinement」算法）同等强大。因此，它甚至无法区分非常简单的非同构图实例。例如，消息传递神经网络无法对三角形进行计数，而这种三角形模体（motif）被认为在社交网络中扮演者重要的角色，它与表示用户「紧密联系」程度的聚类系数息息相关。我们可以设计表达能力更强的图神经网络来模拟越来越强大的 k-WL 测试。然而，这样的架构会导致计算复杂度很高，引入大量的参数。更重要的是，这样的架构往往还需要非局部的操作，这使得它们并不具备可行性。

图 5：无法被 1-WL 检测区分，但是可以被 3-WL 检测区分开来的非同构图示例。这是由于 3-WL 可以对三角形模体进行计数。

因此，基于 WL 层次结构的可证明的强大图神经网络要么性能较弱但较为实用，要么性能强大但并不实用。在作者 Michael Bronstein看来，应该有另外一种简单的的方式设计既高效有可证明的强大图神经网络，我们在与 Giorgos Bouritsas 和 Fabrizio Frasca 等人合作完成的论文「Improving Graph Neural Network Expressivity via Subgraph Isomorphism Counting」中提出了这种方法。

相关论文链接：https://arxiv.org/abs/2006.09252

1、图子结构网络

图子结构网络的思路实际上十分简单，在概念上与位置编码或图元核（graphlet）描述子相似：让消息传递机制感知局部的图结构，使其能够根据末端节点之间的拓扑关系以不同的方式计算消息。这是通过向消息传递函数传递与每个节点关联的附加结构描述子来实现的，这种描述子是通过子图同构计数实现的。通过这种方式，我们可以将图中的节点划分到不同的等价类中，这些等价类反映了每个图内部的节点之间以及跨越不同图的节点之间共享的拓扑特性。

我们将这种架构称为「图子结构网络」（GSN）。该网络与标准的消息传递神经网络拥有相同的算法设计、存储复杂度以及计算复杂度，但是它在构造结构描述子之前增加了一个预计算步骤。选择需要计数的子结构对于 GSN 的表达能力以及预计算步骤的计算复杂度都是至关重要的。

对于包含 n 个节点的图，在对包含 k 个节点的子结构进行计数的过程中，最差的计算复杂度为 𝒪(nᵏ)。因此，这与高阶图神经网络模型或前文中提到的 Morris 和 Maron 所提出的模型相类似。然而，GSN 相较于其它方法具有以下优势：

（1）对于「路径」或「环」等类型的子结构，GSN 可以以明显较低的复杂度进行技术；

（2）具有高昂计算开销的步骤仅仅作为预处理执行一次，因此不会影响网络的训练和推理，正如在消息传递神经网络中一样，网路的训练和推理会保持线性。训练和推理时的存储复杂度也是线性的；

（3）最重要的是，GSN 的表达能力与 k-WL 测试是不同的，在某些情况下，GSN 的表达能力要更强。

2、GSN 有多强大？

子结构计数赋予了 GSN 比标准的消息传递神经网络更强的表达能力。首先，需要说明的是，GSN 的表达能力取决于使用的图的子结构。与 k-WL 测试中的层次结构相同，我们可以基于对一种或多种结构进行计数得到 GSN 的不同的变体。通过使用比星型图更复杂的结构，GSN 可以获得一定强于 1-WL（或等价的 2-WL）更强的能力，因此也比标准的消息传递架构更强。当使用四元团（4-clique）时，GSN 的能力至少不会弱于 3-WL。

在下面的示例中，GSN 在强正则图上仍然有效，而 3-WL 则失效了：

图 6：包含 16 个顶点的非同构强正则图的示例，每个顶点的度为 6，每 2 个邻接的顶点拥有 2 个共同邻居。3-WL 测试在本例中失效，然而使用四元团的 GSN 可以区分这两个图。在左图（被称为「Rook's graph」）中，每个节点都恰好被包含在一个四元团中。右图（Shrikhande graph）则包含三元最大团（三角形）。

更一般来说，对于各种 𝒪(1) 阶的子结构而言，只要不能通过 3-WL 对其进行计数，那么就存在 GSN 能够成功区分而 3-WL 无法区分的图。尽管我们找不出反例，但是原则上这种反例是存在的——这也正是我们稍有顾虑地仅仅将 GSN 的能力表述为「至少不会弱于 3-WL」的原因。

当 k-WL 中的 k 取更大值时，上述结论也成立；上图中的强正则图可以被归纳为「k-iosregular」，它们是 (k+1)-WL 测试失效的实例。使用恰当结构的 GSN 也可以区分这些示例。因此，GSN 的表达能力如下图所示：

图 7：GSN 在 WL 层次结构之外。在使用恰当的结构时（例如，特定规模的团或环），GSN 的能力至少不弱于 k-WL。

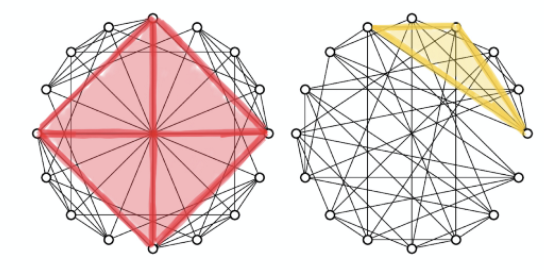
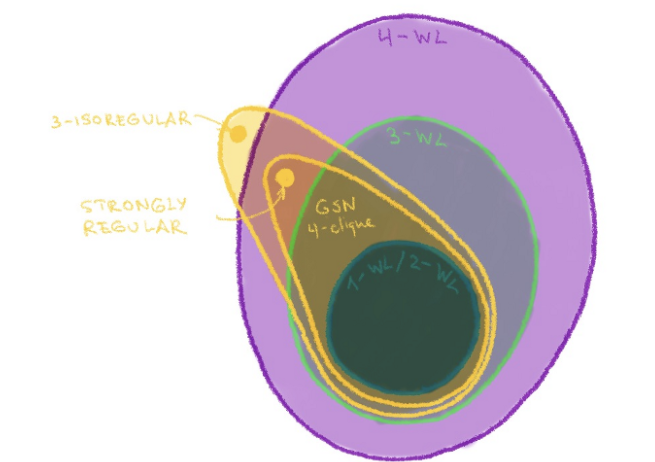
一般来说，GSN 的能力究竟有多强呢？这仍然是一个开放性的问题。图重构猜想（Graph Reconstruction Conjecture）假定了根据一张图的所有删除某些节点后得到的子结构恢复出该图的概率。因此，如果图重构猜想是正确的，那么使用包含 n-1 个节点组成的子结构的 GSN 就可以正确地测试任意图的同构性。然而，到现在为止，人们只在节点数 n≤11 的图上证明了图重构猜想。其次，对如此大的子结构进行计算也是不切实际的。

一个更有趣的问题是，对于「小型」结构（大小为 𝒪(1) 常数阶，与节点数 n 无关）而言，是否存在相似的结果。我们的实验结果证明，使用小型子结构（例如，环、路径、团）的 GSN 对于区分强正则图是有效的，而这对于 WL 测试来说是十分困难的。

最重要的是，GSN 是构建在标准的消息传递架构之上的，因此继承了其局部性和线性复杂度。GSN 的超参数包括为了构建结构描述子而计数的结构。也许，实际的应用会在「需要的表达能力」、「能保证这种表达能力的结构大小」、「计算复杂度」之间进行权衡。

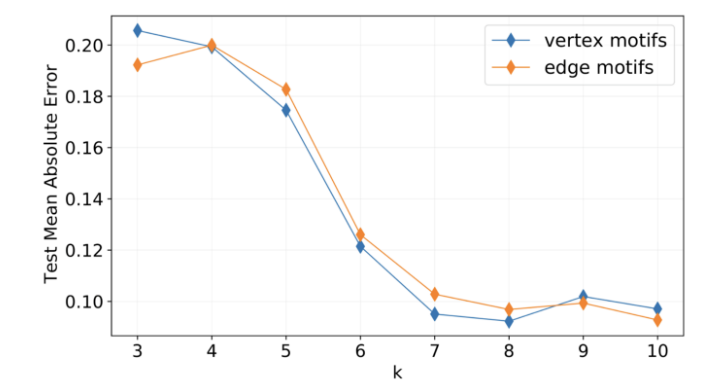
图 8：使用考虑了长度 k≥6 的环结构的 GSN，在 ZINC 数据集中，显著提升了对分子图的化学性质的预测性能。ZINC 数据集被制药公司用于候选药物的虚拟筛查。这种环结构在有机分子中大量存在。

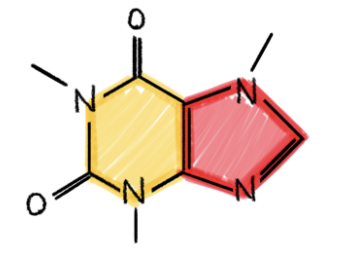
在实验中，我们观察到：不同的子结构会为不同的问题和数据集带来帮助。因此，对于子结构的选择可能需要视具体问题而定。幸运的是，在某些实际应用中，我们往往知道何种子结构是有用的。例如，在社交网络中，三角形和高阶的团是很常见的，并且有明确的「社会学」解释。在化学领域中，环是一种非常常见的模式（例如，五元、六元芳环在大量的有机分子中都存在）。下图显示了一种我们大多数人都很熟悉的示例：咖啡因的分子结构。

图 9：1,3,7—三甲基黄嘌呤，俗称咖啡因，是一种包含五元、六元环（分别表示为红色和黄色）的换装化合物。

3

超越 Weisfeiler-Lehman：近似同构性与度量嵌入

基于图论的在多项式时间内能够求解的算法为图同构问题提供了一种必要不充分条件。在图深度学习领域中，研究人员已经证明了消息传递神经网络和 1-WL 测试的能力相当。采用高阶、更强大的 k-WL 测试可以实现具有高计算复杂度的图神经网络，此时网络涉及非局部操作，而在实际应用程序中，这是不实用的。

Michael Bronstein 近期在论文「Improving graph neural network expressivity via subgraph isomorphism counting 」中介绍了一种不同的方法，它摒弃了 WL 层次结构，转而采用了一种消息传递机制，这种机制可以感知环、团、路径等局部图结构。这使得我们的图神经网络拥有吸引人的局部性以及标准消息传递架构的低计算复杂度。同时，作者可以证明，该网络比 2-WL 更强大，并且至少不弱于 3-WL。这种视角开启了图论领域中，尚未在图神经网络表达性方面被探索过的开放性问题的深层次的联系。

相关论文链接：https://arxiv.org/abs/2006.09252

故事到这里还远未结束。作者表示，他相信，我们可以通过改变看待问题的角度做得更好。

1、近似同构

虽然研究人员已经基于图神经网络与图同构问题的联系产生了一些重要的思路，但是这种设定本身还是相当具有局限性的。我们可以认为图神经网络试图寻找图嵌入 f(G) ，这种嵌入具有我们期望的特性，即 f(G)=f(G′) 当且仅当 G~G′。

不幸的是，由于可以通过 WL 测试是判定图同构的必要非充分条件，上述我们期望得到的特性只有一个方向能说得通：当 G~G′ 时， f(G)=f(G′)，但反之不一定成立：两个非同构的图可能会得出相同的嵌入。

在实际应用中，我们很少处理完全同构的图，而是处理如下图所示的「近似同构」的图：

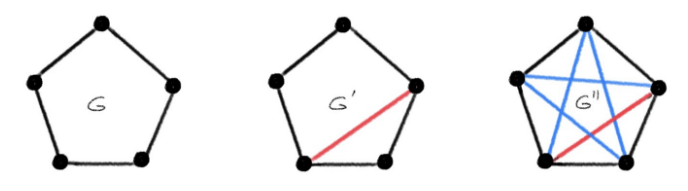
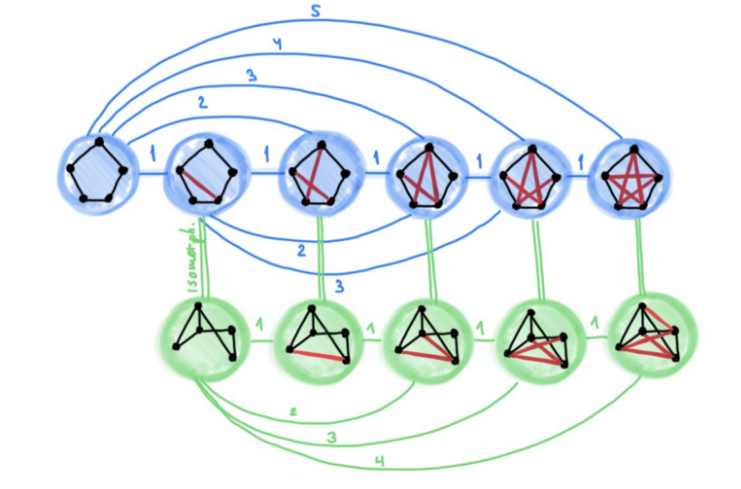
图 10：近似同构图示例：(G, G′)、(G, G″)都是非同构的。但是 G 和 G′ 只有一条边不同，而 G 和 G″ 有五条边不同，因此 G 和 G′ 拥有比 G 和 G″ 之间「更强的同构性」。

我们可以用一种度量指标 d 来量化「近似同构」的概念，当两图不相似时 d 的值较大，而当两图很相似时 d 的值较小。「图编辑距离」或「Gromov-Hausdorff」距离是两种可能的 d 的示例。需要注意的是，该度量标准可以被定义为：d(G,G′)=0 当且仅当 G~G′，即说明两个同构图难以被区分。保距嵌入（isometric embedding）问题：

对于所有的 G, G′，有 |f(G)−f(G′)|=d(G,G′) (♠)

试图使用图嵌入之间的欧氏距离 |.| 替代图的距离，我们要求这两种距离是相等的（在本例中，嵌入 f 是「保距的」）。

图神经网络表达能力的相关工作说明，我们可以在多项式时间内，在 WL 测试有效的一系列图上构建满足 (♠) 的图嵌入。而这一设定似乎限制性太强。第一，也许我们无法设计一种局部的高效算法，保证 (♠) 对于所有图都成立。第二，图同构问题中的性质并不一定在近似同构图上成立（在 d(G,G′)>0 的情况下）。一般而言，更相似的图在嵌入空间中反而较为不相似的情况也是可能存在的，即 d(G,G′)<d(G,G″) 但 |f(G)−f(G′)|>|f(G)−f(G″)|。

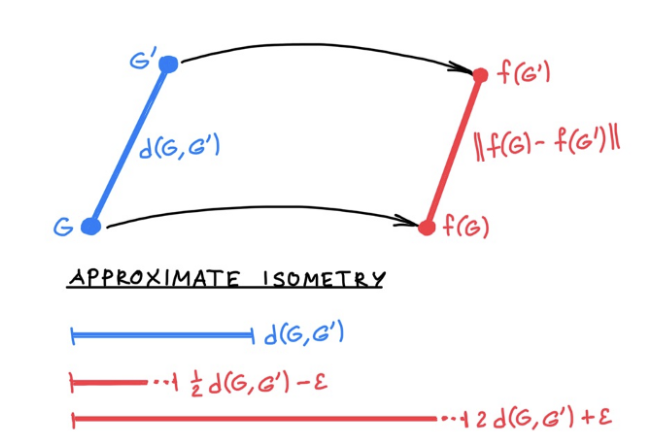
但是另一方面，对度量的形式化定义却提供了更大的灵活性。我们不必要求 (♠) 一定成立，可以通过规定「度量膨胀」（metric dilation）的界对其进行松弛：

当 c≥1 时，c⁻¹ d(G,G′) ≤ |f(G)−f(G′)| ≤ c d(G,G′) (♣)

它可以被表示为嵌入 f 的双 Lipschitz 常数。这意味着该嵌入不会使用比 c 大的因子「拉长」或「缩短」真实的图距离。

这种嵌入被称为「近似保距」。我们希望得到独立于图（特别是与定点数无关）的界 c。请注意，由于对于同构的图 G~G′，我们有 d(G,G′) 且 f(G)=f(G′)，因此图同构是 (♣) 的特例。如前文所述，在所有图上实现这种近似保距是不可能的。然而，我们可以允许额外的度量失真 ε，从而使模型 (♣) 可以被进一步松弛：

当 c≥1时，c⁻¹ d(G,G′)−ε ≤ |f(G)−f(G′)| ≤ c d(G,G′)+ε (♦)

它设置了一个同构图之间距离的容忍度。如果可以满足(♦)的图要比可以满足 (♠) 的图多得多，那么对于许多应用程序来说，这是一个很小的代价。