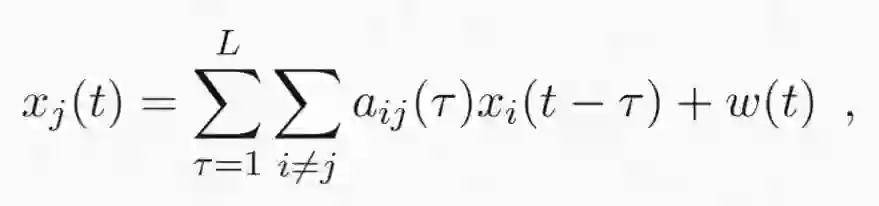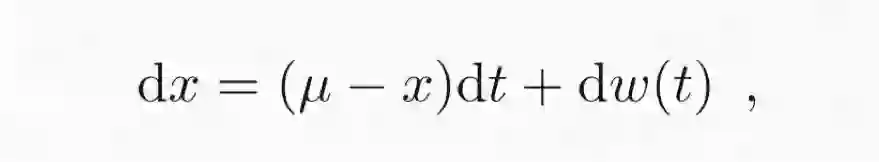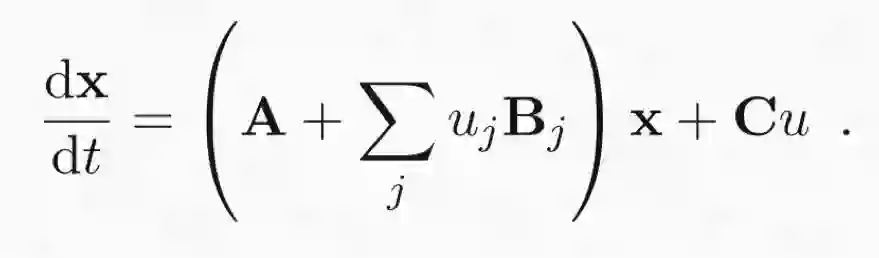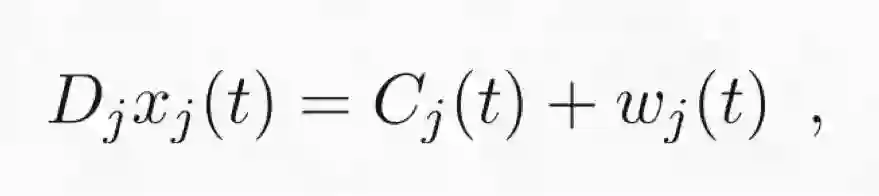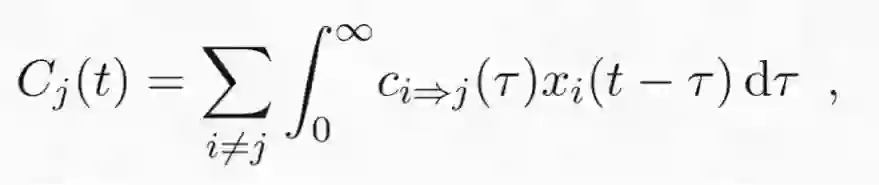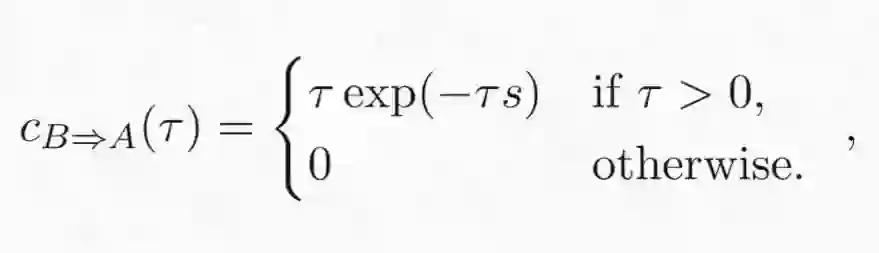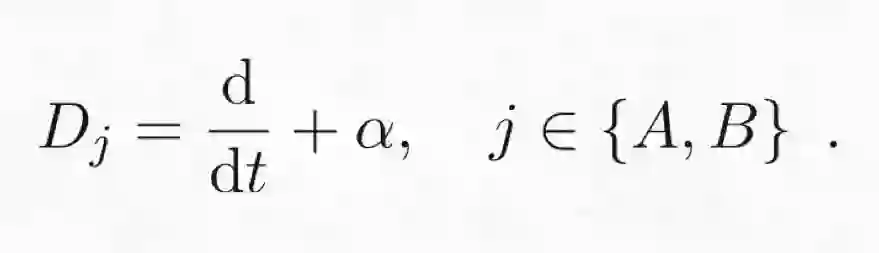深度 | 使用高斯过程的因果推理：GP CaKe 的基本思路

2018 年 11 月 7 日 机器之心

选自mindcodec

机器之心编译

参与：Panda

荷兰拉德堡德大学的研究者的一篇 NIPS 2017 论文基于对大脑中因果交互的研究，提出了一种用于因果推理的通用方法 GP CaKe。日前，相关研究者开始通过一系列文章讲解这种融合了向量自回归模型与动态因果建模两者之长的新方法的思路及其应用。本文为该系列的第一篇，阐释了 GP CaKe 的设计思路。

项目地址：https://github.com/LucaAmbrogioni/GP-CaKe-project
原论文：http://papers.nips.cc/paper/6696-gp-cake-effective-brain-connectivity-with-causal-kernels.pdf

我们最近开发出了一种用于时间序列数据中因果推理的全新方法 [Ambrogioni et al., 2017]。我们称之为「GP CaKe」，即具有因果核的高斯过程（Gaussian Processes with Causal Kernels）。这种方法不仅缩写词（有「蛋糕」的意思）很美味，而且将向量自回归模型（VAR）那引人注目的特性与动态因果建模（DCM）优雅地结合到了一起。是的，确实是一举两得！

我们最初是为研究心智中的有效连接（即大脑区域之间的因果交互研究）而开发了这种方法，但该方法是完全通用型的，也能用在其它任何地方 [1]。我将通过一个文章系列来解释 GP CaKe 背后的思想，本文是其中第一篇。在接下来的文章中，我将通过逐步讲解的方式解释如何使用我们在 GitHub 上提供的代码，之后我还将扩展介绍这个模型的延伸方法。

背景：对多变量时间序列的分析

这项研究的研究背景是带有一个时间维度的复杂系统。在我们的案例中可能是对多个大脑区域的激活状态的连续测量，比如通过 EEG、MEG 或 fMRI [2] 等方式，但也可以是连续的股票交易列表、天气现象以及蛋白质浓度变化等等。

在统计学和机器学习领域，建模这种复杂系统的时间序列的方法主要有两种：向量自回归（VAR）[Lütkepohl, 2005] 和动态系统理论（DST），后者通常是通过（随机）微分方程（SDE）或差分方程 [Abraham & Shaw, 1983] 实现的。我们将简要介绍这两种方法，以激发你的兴趣以及说明 GP CaKe 与它们的关联。如果你已经很了解这两种方法了，可以直接跳过这部分，查看后文有关 GP CaKe 的内容。

向量自回归

向量自回归（VAR）最基本的形式是预测一个特定变量 x_j(t) 在时间 t 的值，该变量是另一些变量 x_i 的（随机）函数，它们的关系如下 [3]：

这个等式的含义如下：

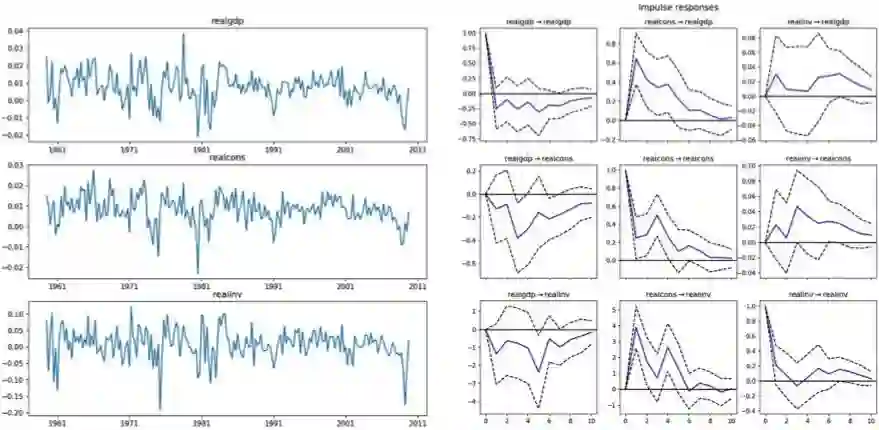
变量 x_j(t) 的信号取决于该变量从所有其它变量获得的输入。这种依赖关系的强度由自回归系数 a_ij(τ) 确定。参数 τ 是信号 x_j(t) 和 x_i(t) 之间的延后量（lag）。综合起来，这表示一个变量对另一个变量的影响可以在 τ=0 时为零（举个例子），然后这种因果影响会缓慢增大（即 a_ij(τ) 更大），只有当延后量变得很大时才会再次衰减——这意味着在遥远过去发生的某些事情现在已经不再重要了。如果我们绘制出这些系数与该延后量的函数关系，我们就会得到所谓的脉冲响应函数（impulse response function/IRF）。最后，w(t) 描述的是驱动系统的随机「创新量（innovations）」或「冲击量（shocks）」。它们能够反映 x_j(t) 的内部动态。比如说，我们国家的天气会受周边邻国天气状况的影响（即它们对我们的气候有因果影响），但也会受到我国内部情况的影响。如果 a_ij(τ)>0，我们就可以说 x_i 对 x_j 有因果影响（这一思想的实际实现将需要某些显著性测试）。这意味着因果关系的时间概念：一个变量的过去能为我们提供有关另一个变量的未来的信息。这种看待因果关系的角度也被称为 Wiener-Granger 因果关系，有时也被简称为 Granger 因果关系 [Bressler & Seth, 2011]。通过观察 IRF，我们可以明确地看到 Granger 因果交互的时间形状：

图 1：在三大金融指数上的 VAR 分析示例。左图是每个变量的时间序列，右图是最大为 10 个月的延后量的脉冲响应函数（IRF）。注意其中也包含了自响应。

动态系统理论

顾名思义，动态系统理论（DST）也就是建模了系统的动态。以经典的 Ornstein-Uhlenbeck 过程为例，如下所示：

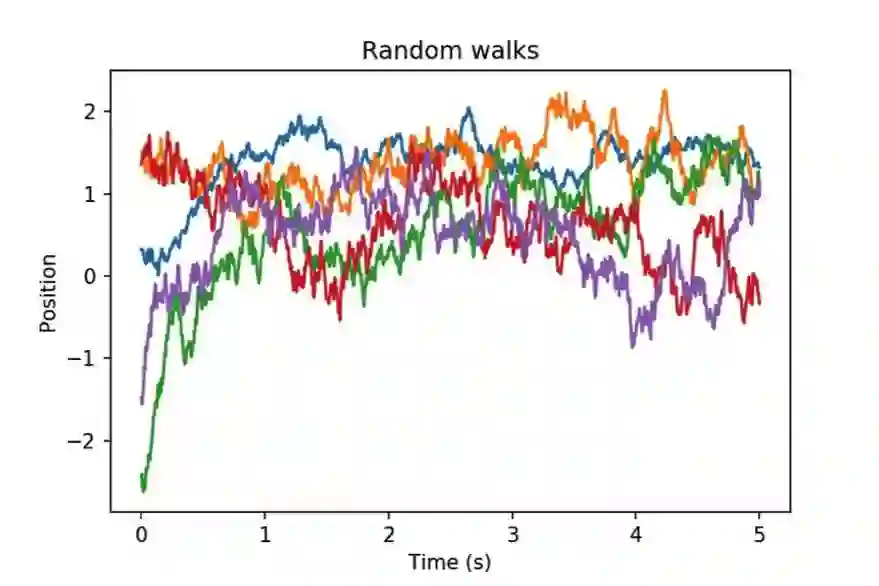
这描述了一个随机游走过程——随着时间推移，会逐渐趋近其平均值 μ。

图 2：五个全都（渐进地）回到同一平均值 μ=0.8 的 Ornstein-Uhlenbeck 过程，但它们各自的噪声水平和回到均值的速度都各不相同。

DST 在动态因果建模（DCM）方面也有应用 [Friston, 2009]。尽管 DCM 的大多数实现都包含一个专用于 fMRI 的前向模型，将 DCM 的应用限制在了神经成像研究领域，但其核心有一个通用型的微分方程系统：

注意，其中 X=(x_1, ..., x_n)。此外，A 是一个包含 x 中变量之间固定交互的矩阵。其作用类似于 VAR 模型的自回归系数，但 DCM 中没有建模延后量。实际上，其动态所受的影响是即时的。另外的 B 和 C 项表示（节点特定的）外源输入 μ，我们这里不会对此详做讨论，因为 GP CaKe [4] 中（尚）没有与这些项类同的地方。

连续和动态的向量自回归：GP CaKe

前提内容已经足够了，现在该进入正题了 [5]。VAR 模型的难点是在实际操作中，我们没有足够多的观察来可靠地估计自回归系数。由此造成我们的脉冲响应函数充满噪声且难以解读。此外，VAR 模型只能粗略地描述系统的动态。高阶交互会被完全忽视。DCM 确实能更广泛地考虑动态，但是它却不能建模一个变量的变化和另一个变量的动态的变化之间的延迟情况，这是有问题的。DCM 的某些变体确实包含一个延后项，但会将其设置为一个常量项，而不是我们估计交互系数的值的一个区间。你可能也已经猜到了：GP CaKe 实际上将延后的交互与动态系统结合了起来。下面来一窥究竟。

GP CaKe 的组成可写成如下形式：

其中，D_j 是微分算子（即其描述了直到第 p 个导数的动态），w_j(t) 仍然是指「创新量（innovation）」或「冲击量（shock）」项，关键的 C_j(t) 是来自其它变量 i≠j 的因果效应的总和。

其中，C_i(t) 到 C_j(t) 是因果脉冲响应函数（CIRF），描述了从 i 到 j 的因果交互。从中可以看到，C_j(t) 是时间序列的求和（在所有输入变量上），并且这些时间序列与它们的脉冲响应函数进行了卷积。这个定义完全类似于 VAR 模型等式右侧的第一项，但却是连续的，而非离散的。然而，GP CaKe 并不简单地是 VAR 的连续式变体。微分算子 D_j 看似没啥作用，但实际非常关键。它描述的是一个变量的内部动态，且无论它从其它变量那里得到了什么输入——而且我们尚未描述这些动态是什么！存在一些（实际上数量很有限）可能的选项，比如，这些动态可以是我们之前见过的简单的 Ornstein-Uhlenbeck 随机游走，即一个振荡过程。不管是在什么案例中，都要记住这样一个重点：GP CaKe 假设来自其它变量的输入会通过因果脉冲响应函数影响动态 D_jx_j(t)，而不只会影响 x_j(t) 本身！

让我们实现它

在下一篇文章中，我将解释如何计算因果脉冲响应函数，这与我们之前的一篇有关高斯过程回归中傅立叶变换的文章有关：https://www.mindcodec.com/the-fourier-transform-through-the-lens-of-gaussian-process-regression/。目前，我们就假设我们已经有能帮助我们完成这项任务的工具了（实际上我们确实有，参见对应的 GitHub 项目）。我们这里只是为了进行一点演示，不会涉及太多细节。我们将使用一个已知的脉冲响应函数来生成某些数据，然后会尝试使用 VAR 和 GP CaKe 来恢复它。注意，目前已经存在一些比标准的非正则化的 VAR 更好的实现，但这里只是用于解释说明，普通的 VAR 就足够了。

我们从两个变量 x_A 和 x_B 开始，它们具有如下的因果关系：

其中 τ 仍然是两个变量之间的时间延后量，而 s 则是脉冲响应的长度范围（这个函数的形状如下图中的红线所示）。为了我们当前的目的，这是一个任意的变量，我们只是随便选取了某个值。此外，我们假设这两个变量的内部动态都是 Ornstein-Uhlenbeck 过程，因此

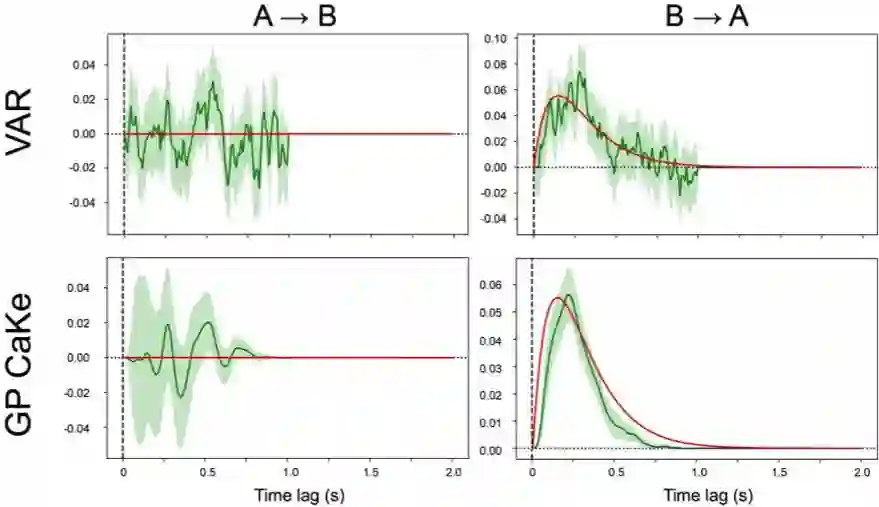
其中，α 是该过程的弛豫系数，指示了该时间序列回到其均值（零）的速度。我们为该动态系统生成了 100 个样本，总长度为 4 秒，采样频率为 100 Hz。然后我们使用一个延后量为 100（即 1 秒）的 VAR 模型与 GP CaKe 模型恢复这个脉冲响应函数。GP CaKe 有三个重要参数，分别反映了其响应函数的时间平滑度、时间定位和噪声水平，我们会在下一篇文章详细讨论它们。现在，我直接用人工方式将这些参数设置成合理的值；在实际应用时，我们会根据数据来估计它们的值，并通过相关应用的背景知识来设置它们。图 3 展示了模拟实验的结果。可以看到，这两种方法都可以很好地区分当前存在的和不存在的连接（注意图中的纵轴是不一样的）。对于当前存在的连接，这两种方法都能在一定程度上恢复它的形状；但 GP CaKe 的结果比 VAR 的结果更加平滑且更为可靠。另外，这个响应函数在 1 秒之后没有突然的断点。