不可错过！「强化学习导论」多伦多大学2021课程，附SLIDES与140页pdf笔记

2021 年 3 月 24 日 专知

最新《强化学习》干货课程！

这是一门关于在不确定情况下强化学习(RL)和顺序决策的入门课程，重点在于理解理论基础。我们研究如何使用动态规划方法，如价值和策略迭代，来解决具有已知模型的顺序决策问题，以及如何扩展这些方法，以解决模型未知的强化学习问题。其他主题包括(但不限于)RL中的函数近似、策略梯度方法、基于模型的RL以及平衡探索-利用权衡。本课程将以讲座和阅读古典及近期论文的方式传授给学生。因为重点是理解基础，你应该期望通过数学细节和证明。本课程的要求背景包括熟悉概率论和统计、微积分、线性代数、最优化和(有监督的)机器学习。

https://amfarahmand.github.io/IntroRL/

1 (Jan 12)	Introduction to Reinforcement Learning
2 (Jan 19)	Structural Properties of Markov Decision Processes (Part I)
3 (Jan 26)	Structural Properties of Markov Decision Processes (Part II)
4 (Feb 2)	Planning with a Known Model
5 (Feb 9)	Learning from a Stream of Data (Part I)
6 (Feb 25)	Learning from a Stream of Data (Part II) Value Function Approximation (Part I)
7 (Mar 2)	Value Function Approximation (Part II)
8 (Mar 9)	Value Function Approximation (Part III)
9 (Mar 16)	Value Function Approximation (Part IV)
10 (Mar 25)	Policy Gradient Methods
11 (Mar 30)	Model-based RL
12 (April 6)	Presentations

强化学习入门笔记

这是多伦多大学计算机科学系于2021年春季教授的强化学习(RL)研究生课程介绍的讲义。本课程是入门性的，因为它不需要预先接触强化学习。然而，它不仅仅是算法的集合。相反，它试图在RL中经常遇到的许多重要思想和概念背后建立数学直觉。在这些讲义的过程中，我证明了很多基础的，或者有时不那么基础的，RL的结果。如果某个结果的证明过于复杂，我就证明一个简化的版本。

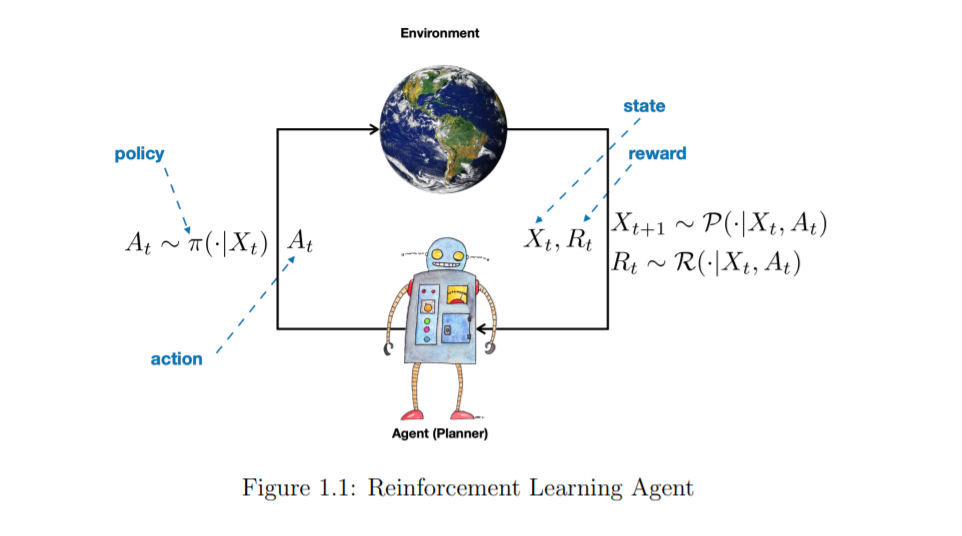
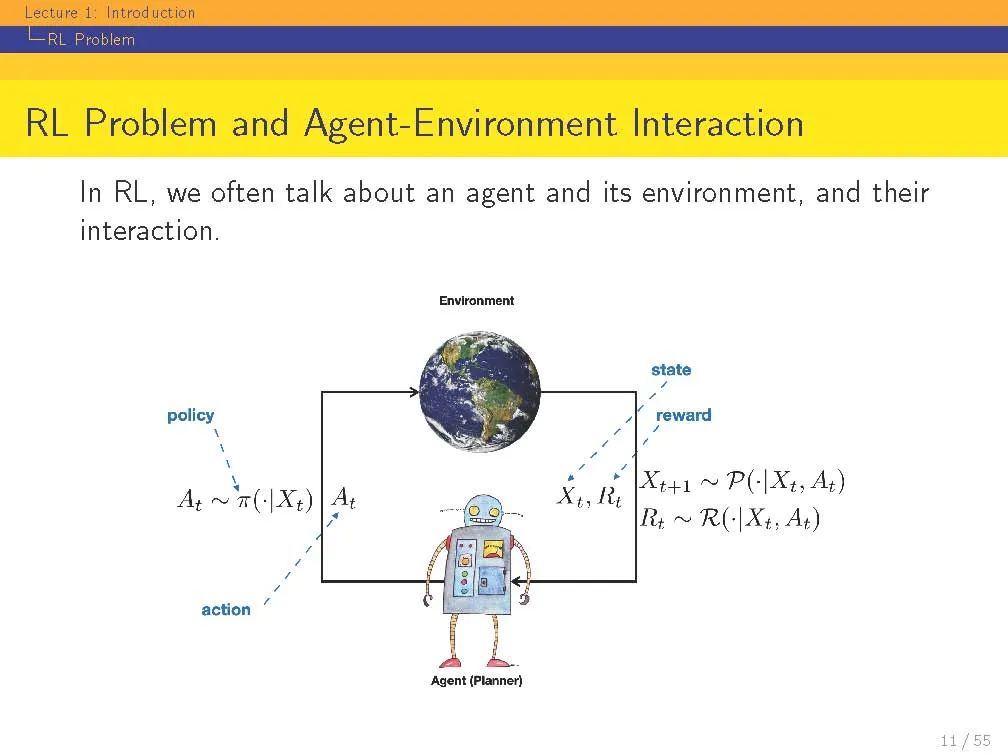
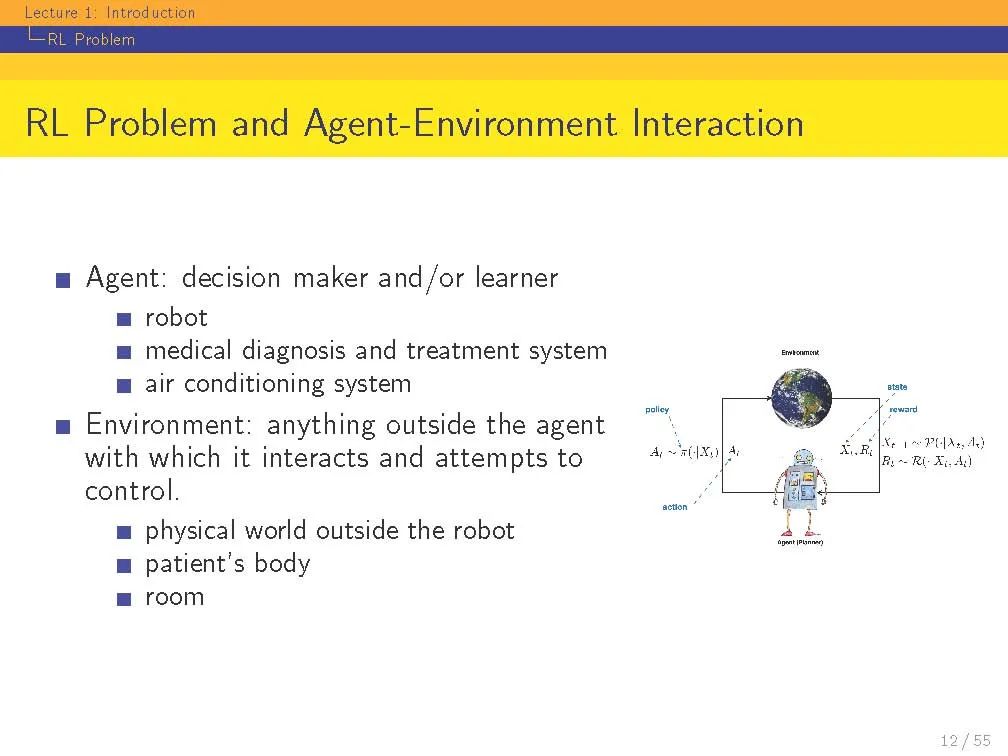
强化学习(RL)既指一类问题，也指解决这类问题的一组计算方法。RL问题是指如何采取行动，使某些长期绩效的概念得到最大化。RL问题，从它的定义来看，是关于一个实体的行为和交互，我们称之为代理，与其周围的环境，我们称之为环境。这是一个非常普遍的目标。有人可能会说，解决AI问题等同于解决RL问题。强化学习也指解决RL问题的一套计算方法。一个代理需要做什么样的计算才能确保它的行为能够带来良好的(甚至是最佳的)长期性能?实现这些的方法称为RL方法。历史上，在所有试图解决RL问题的计算方法中，只有一个子集被称为RL方法。例如Q-Learning这样的方法(我们将在本课程中学习)是一种很好的RL方法，但是进化计算的方法，如遗传算法，则不是。人们可以争辩说，进化计算方法没有太多的“学习”成分，或者它们不以个体生命的时间尺度行事，而是以世代的时间尺度行事。虽然这些是真正的区别，但这种划分方式有些武断。在本课堂讲稿中，我们将重点放在“RL社区”中经常学习的方法上。