统计学常用数据类型

作者： Niklas Donges

编译：weakish

编者按：数据类型是统计学的重要概念。机器学习和数据科学开发者Niklas Donges简要介绍了不同的数据类型，理解这些数据类型有助于对数据集进行恰当的探索性数据分析（EDA）——机器学习项目最被低估的部分之一。

介绍

理解不同的数据类型，是探索性数据分析（Exploratory Data Analysis，EDA）所需的关键预备知识，同时也有助于你选择正确的可视化方法。你可以将数据类型看成归类不同类型变量的方式。我们将讨论主要的变量类型，以及相应的示例。有时我们会称其为测量尺度（measurement scale）。

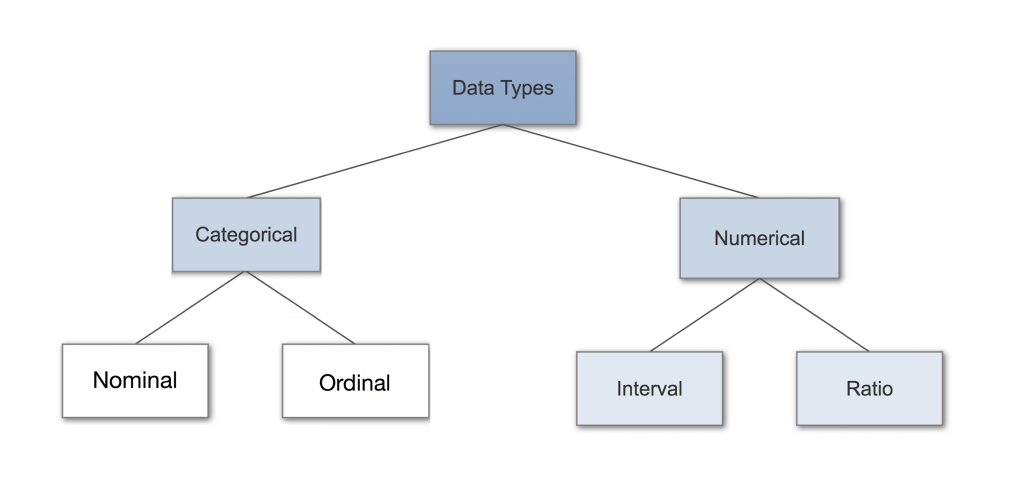
类别数据

类别数据（categrorical data）表示特性，例如一个人的性别，所说的语言，等等。类别数据同样可以使用数值（例如：1表示雌性，0表示雄性）。

名目数据

名目值（nominal value）指用于标记变量的定性离散单元。你可以直接把它们想象成“标签”。注意名目数据是无序的。因此，如果你改变名目值的顺序，其语义并不会改变。下面是一些名目特征的例子：

• 性别：雌性、雄性。

• 语言：英语、法语、德语、西班牙语。

上面的性别特征也被称为“二分（dichotomous）”值，因为它只包含两个类别。

次序数据

次序值（ordinal value）指离散、有序的定性单元。除了有序之外，它几乎和名目数据一样。例如，教育背景可以用次序值来表示：

1. 初中

2. 高中

3. 大学

4. 研究生

注意，其实初中、高中之间的差别，和高中、大学之间的差别，是不一样的。这是次序数据的主要限制，次序值之间的差别是未知的。因此，次序值通常用于衡量非数值特征，例如愉悦程度、客户满意度。

数值数据

离散数据

离散数据（discrete data）的值是不同而分散的，换句话说，只能接受一些特定值。这类数据无法测量但可以计数。它基本上用来表示可以分类的信息。例如，抛100次硬币正面向上的次数。

你可以通过以下两个问题检查你处理的是否是离散数据：你可以对其计数吗？它可以被切分成越来越小的部分吗？

相反，如果数据可以测量但无法计数，那就是连续数据。

连续数据

连续数据（continuous data）表示测量。例如身高。

连续数据可以分为等距数据（interval data）和等比数据（ratio data）。

等距值指间隔相等的有序单元，也就是说，等距变量包含有序数值，并且我们知道这些数值之间的间隔。例如，用等距数据表示温度：

1. -10

2. -5

3. 0

4. +5

5. +10

6. +15

等距值的问题在于，它们没有“真正的零”。拿上面的例子来说，0度不是绝对零度。另外，我们可以加减等距值，而不能乘除等距值或计算比率。由于没有“真正的零”，无法应用许多描述统计学或推论统计学的方法。

等比值具有等距值的所有特性，同时也有绝对的零。因此，不仅可以加减，还可以乘除。高度、重量、长度、绝对温度等都属于等比值。

数据类型为什么重要？

数据类型是一个非常重要的概念，因为统计学方法只能应用于特定的数据类型。你需要使用不同的方式分析连续数据和类别数据。因此，理解你处理的数据的类型，让你能够选择正确的分析方法。

下面我们将重新查看上面提到的每种数据类型，了解它们可以应用什么样的统计学方法。为了理解我们将讨论的一些性质，你需要对描述性统计学有所了解。如果你对此不熟悉，可以先看下我写的描述性统计学介绍。

统计学方法

名目数据

处理名目数据时，你通过下述方式收集信息：

• 频数 在一段时间内或整个数据集中出现的次数。

• 比例 频数除以所有事件的频数之和，即可得到比例。

• 百分比 我想这无需解释了吧。

• 众数 出现次数最多，也就是频数最高的数据。

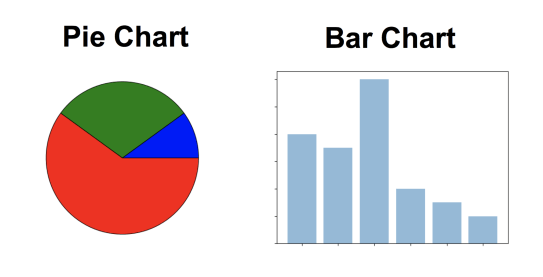
• 可视化方法 你可以使用饼图或直方图可视化名目数据。

左：饼图；右：直方图

次序数据

当你处理次序数据时，你可以使用以上用于名目数据的方法，不过，除此之外，你还可以使用一些额外的工具。也就是说，你可以使用频数、比例、百分比、众数概括次序数据，也可以使用饼图、直方图可视化次序数据。除此之外，你还可以使用：

• 百分位数 计算由小到大排列的次序数据的累计百分位，某一百分位对应的数据值就称为这一百分位的百分位数。百分位数可以用来描述数据的离散趋势。

• 中位数 即第50百分位数，它将数据分为相等的上下两部分。中位数可以用来描述数据的中间趋势。例如，如果我们用次序数据表示星巴克咖啡的容量：中杯、大杯、特大杯。那么，其中位数为大杯（也就是说，真正的中杯是大杯）。

• 四分位距 第75百分位数与第25百分位数之差即为四分位距。四分位距可以简要概述数据的离散趋势。

连续数据

大多数统计学方法都可以用于连续数据。你可以使用百分位数、中位数、四分位距、均值、众数、标准差、区间。

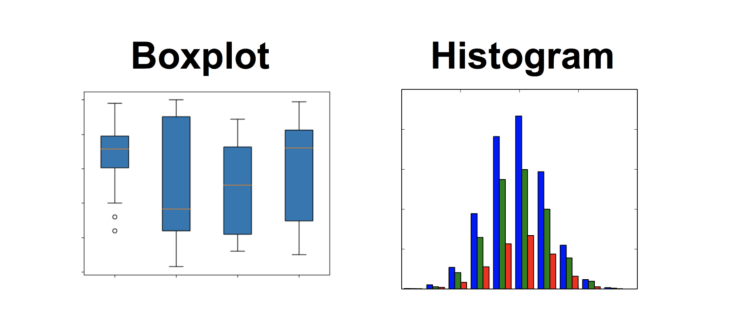
你可以使用矩形图或箱形图可视化连续数据。从矩形图上可以看到分布的中间趋势、离散程度、形态和峰态。注意，矩形图不体现离散值，因此我们有时使用箱形图。

左：箱形图；右：矩形图

总结

本文讨论了统计学中常用的不同数据类型。你了解了离散数据和连续数据的区别，以及什么是名目数据、次序数据、等距数据、等比数据。此外，你现在知道了每种数据类型可以应用的统计学方法和可视化方法。如果你在给定数据集上进行探索性分析，你会发现这些非常有用。

原文地址：https://machinelearning-blog.com/2018/03/07/data-types-in-statistics/