机器学习方案(技巧)手册

This was a busy week, I had no time to read anything new, so I'm sharing a note that I wrote for myself, for no other reason than to understand things better. It's a kind of cookbook of various "transformations" you can apply to a machine learning problem to eventually turn it into something we know how to solve: seeking stable attractors of a tractable vector field.

The typical setup is: you have some model parameters  θ θ . You seek to optimize some objective criterion, but the optimization problem is intractable or hard in one of the ways listed below. You then apply the corresponding transformation to your problem if you can. If your problem is now one you can efficiently optimize, great. If not, you can recursively apply the transformations until it is.

UPDATE: Although I called this post a cookbook, as readers so rightly pointed out, it is too light on details to be considered a cookbook. Consider it as a demonstration of a way of thinking about machine learning research as a compiler that compiles an abstract machine learning objective into the canonical optimization problem of finding stable attractors of a tractable vector field.

For the first batch, I have written up the following problem transformations:

• Variational bounds

• Adversarial games

• Evolution Strategies

• Convex relaxation

There are many more transformations not included here, like the duality principle, half-quadratic splitting, Lagrangian multipliers, etc. Feel free to leave comments about what else I should include next.

Variational bounds

Typical problem:

My loss function 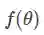 is intractable to compute, typically because it involves intractable marginalization. I can't evaluate it let alone minimize it.

Solution:

Let's construct a family of - typically differentiable - upper-bounds: 

and solve the optimization problem 

转自：inFERENCe

完整内容请点击“阅读原文”